Leha decided to move to a quiet town Vičkopolis, because he was tired by living in Bankopolis. Upon arrival he immediately began to expand his network of hacked computers. During the week Leha managed to get access to n computers throughout the town. Incidentally all the computers, which were hacked by Leha, lie on the same straight line, due to the reason that there is the only one straight street in Vičkopolis.
Let's denote the coordinate system on this street. Besides let's number all the hacked computers with integers from 1 to n. So the i-th hacked computer is located at the point xi. Moreover the coordinates of all computers are distinct.
Leha is determined to have a little rest after a hard week. Therefore he is going to invite his friend Noora to a restaurant. However the girl agrees to go on a date with the only one condition: Leha have to solve a simple task.
Leha should calculate a sum of F(a) for all a, where a is a non-empty subset of the set, that consists of all hacked computers. Formally, let's denote A the set of all integers from 1 to n. Noora asks the hacker to find value of the expression 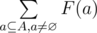 . Here F(a) is calculated as the maximum among the distances between all pairs of computers from the set a. Formally,
. Here F(a) is calculated as the maximum among the distances between all pairs of computers from the set a. Formally, 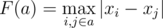 . Since the required sum can be quite large Noora asks to find it modulo 109 + 7.
. Since the required sum can be quite large Noora asks to find it modulo 109 + 7.
Though, Leha is too tired. Consequently he is not able to solve this task. Help the hacker to attend a date.
The first line contains one integer n (1 ≤ n ≤ 3·105) denoting the number of hacked computers.
The second line contains n integers x1, x2, ..., xn (1 ≤ xi ≤ 109) denoting the coordinates of hacked computers. It is guaranteed that all xi are distinct.
Print a single integer — the required sum modulo 109 + 7.
2
4 7
3
3
4 3 1
9
There are three non-empty subsets in the first sample test: ,
,  and
and 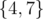 . The first and the second subset increase the sum by 0and the third subset increases the sum by 7 - 4 = 3. In total the answer is 0 + 0 + 3 = 3.
. The first and the second subset increase the sum by 0and the third subset increases the sum by 7 - 4 = 3. In total the answer is 0 + 0 + 3 = 3.
There are seven non-empty subsets in the second sample test. Among them only the following subsets increase the answer: 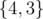 ,
, 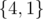 ,
, 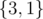 ,
, 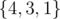 . In total the sum is (4 - 3) + (4 - 1) + (3 - 1) + (4 - 1) = 9.
. In total the sum is (4 - 3) + (4 - 1) + (3 - 1) + (4 - 1) = 9.
由于求子集最大值最小值之间关系,首先肯定排序 这样好找规律。
从小到大排:
{1 3 4} 注意到对于每个数字
1 被当作最小值(被减去) 的次数为 后面{3 4 } 子集数 就是 2^2
1被当作最大值 (增加) 的次数为 {} 的子集 就是2^0
同理找规律
sum = sigma( a[i]*(2^i-2^(n-i) )
#include<iostream> #include<cstdio> #include<cmath> #include<cstring> #include<sstream> #include<algorithm> #include<queue> #include<deque> #include<iomanip> #include<vector> #include<cmath> #include<map> #include<stack> #include<set> #include<fstream> #include<memory> #include<list> #include<string> using namespace std; typedef long long LL; typedef unsigned long long ULL; #define MAXN 100005*3 #define N 21 #define MOD 1000000007 #define INF 1000000009 const double eps = 1e-8; const double PI = acos(-1.0); LL n, a[MAXN], r[MAXN], sum = 0; int main() { scanf("%lld", &n); r[0] = 1; for (int i = 0; i < n; i++) { cin >> a[i], r[i + 1] = (r[i] * 2) % MOD; } sort(a, a + n); for (int i = 0; i<n; i++) { sum += (a[i] * (r[i] - r[n - i - 1])) % MOD; sum %= MOD; } printf("%lld ", sum%MOD); }