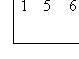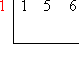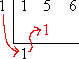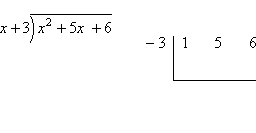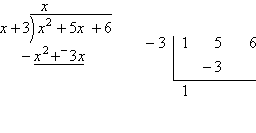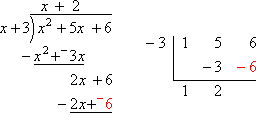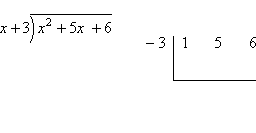synthetic division

Synthetic Division: The Process (page 1 of 4)

Sections:Introduction, Worked examples, Finding zeroes, Factoring polynomials

---

Synthetic division is a shorthand, or shortcut, method of polynomial division in the special case of dividing by a linear factor -- and it only works in this case. Synthetic division is generally used, however, not for dividing out factors but for finding zeroes (or roots) of polynomials. More about this later.

If you are given, say, the polynomial equation y = x² + 5x + 6, you can factor the polynomial as y = (x+ 3)(x + 2). Then you can find the zeroes of y by setting each factor equal to zero and solving. You will find that x = –2 and x = –3 are the two zeroes of y.

You can, however, also work backwards from the zeroes to find the originating polynomial. For instance, if you are given that x = –2 and x = –3 are the zeroes of a quadratic, then you know that x + 2 = 0, sox + 2 is a factor, and x + 3 = 0, so x + 3 is a factor. Therefore, you know that the quadratic must be of the form y = a(x + 3)(x + 2).

Anyway, the above is a long-winded way of saying that, if x – n is a factor, then x = nis a zero, and ifx = n is a zero, then x – n is a factor. And this is the fact you use when you do synthetic division.(The extra number "a" in that last sentence is in there because, when you are working backwards from the zeroes, you don't know toward which quadratic you're working. For any non-zero value of "a", your quadratic will still have the same zeroes. But the issue of the value of "a" is just a technical consideration; as long as you see the relationship between the zeroes and the factors, that's all you really need to know for this lesson.)

Let's look again at the quadratic from above: y = x² + 5x + 6. From the Rational Roots Test, you know that ± 1, 2, 3, and 6 are possible zeroes of the quadratic. (And, from the factoring above, you know that the zeroes are, in fact, –3 and –2.) How would you use synthetic division to check the potential zeroes? Well, think about how long polynomial divison works. If we guess that x = 1 is a zero, then this means that x – 1 is a factor of the quadratic. And if it's a factor, then it will divide out evenly; that is, if we divide x² + 5x + 6 by x – 1, we would get a zero remainder. Let's check:

As expected (since we know that x – 1 is not a factor), we got a non-zero remainder. What does this look like in synthetic division? Copyright © Elizabeth Stapel 2002-2011 All Rights Reserved

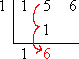
First, write the coefficients ONLY inside an upside-down division symbol:
Make sure you leave room inside, underneath the row of coefficients, to write another row of numbers later.
Put the test zero, x = 1, at the left:
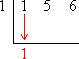
Take the first number inside, representing the leading coefficient, and carry it down, unchanged, to below the division symbol:
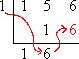
Multiply this carry-down value by the test zero, and carry the result up into the next column:
Add down the column:
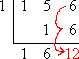
Multiply the previous carry-down value by the test zero, and carry the new result up into the last column:
Add down the column: This last carry-down value is the remainder.

Comparing, you can see that we got the same result from the synthetic division, the same quotient (namely, 1x + 6) and the same remainder at the end (namely, 12), as when we did the long division:

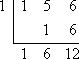The results are formatted differently, but you should recognize that each format provided us with the result, being a quotient of x + 6, and a remainder of 12.

You already know (from the factoring above) that x+ 3 is a factor of the polynomial, and therefore thatx = –3 is a zero. Now compare the results of long division and synthetic division when we use the factor x + 3 (for the long division) and the zero x = –3 (for the synthetic division):

As you can see above, while the results are formatted differently, the results are otherwise the same:

In the long division, I divided by the factor x + 3, and arrived at the result of x + 2 with a remainder of zero. This means that x + 3 is a factor, and that x + 2 is left after factoring out the x + 3. Setting the factors equal to zero, I get that x = –3 and x = –2 are the zeroes of the quadratic.

In the synthetic division, I divided by x = –3, and arrived at the same result of x + 2 with a remainder of zero. Because the remainder is zero, this means that x + 3 is a factor and x = –3 is a zero. Also, because of the zero remainder, x + 2 is the remaining factor after division. Setting this equal to zero, I get that x = –2 is the other zero of the quadratic.

I will return to this relationship between factors and zeroes throughout what follows; the two topics are inextricably intertwined.

picked from  :http://www.purplemath.com/modules/synthdiv.htm