红黑树学习笔记

一、什么样的树才是“合格”的红黑树？

1. 树的根节点都是黑色的
2. 每个叶子节点都是黑色的空节点
3. 任何相邻的节点都不能为连续的红色节点（比如父节点是红色的，他的左子节点或者右子节点都不能为红色）
4. 每个节点，从该节点到达其可达的叶子节点路径上都包含相同数目的黑色节点

二、什么是左旋和右旋啊？

左旋全称其实是叫围绕某个节点的左旋，右旋的全程就是围绕某个节点的右旋。

画个图来展示什么是围绕X节点的左旋和右旋

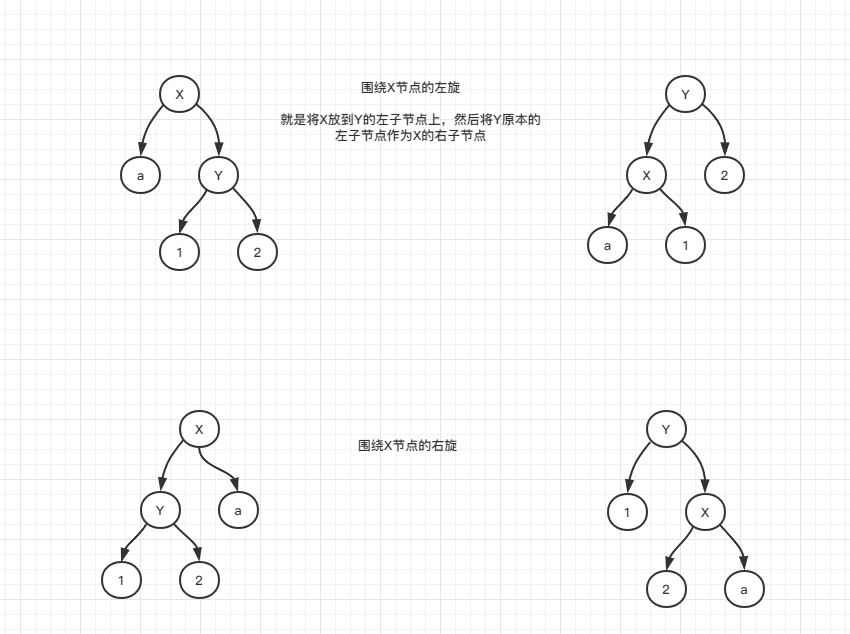
看明白了吗？我们再来一个比较“复杂”的。围绕A节点的右旋操作

三、 红黑树的插入操作逻辑是什么？

为了方便书写，我们下面将所有的R表示红色，B表示黑色，树中的所有节点我统一使用小写字母避免冲突。例如节点b的意思是有一个值的b的节点；节点为B或者说节点B是指这个节点是黑色节点。

1. 红黑树的插入原则

1. 红黑树中插入的节点都是R
2. 插入的节点都是直接放在黑色的空的叶子节点山

按照这个逻辑以及【什么样的树才是"合格"的红黑树】的要求，那么出现以下两种情况是比较好处理的：

1. 如果插入的节点的父节点是黑色的，那我们什么都不用做，只需要给插入的红节点初始化两个颜色为黑、值为null的左右子树即可
2. 如果插入的节点是根节点，那么只需要将其改为黑色即可

2.红黑树的迭代过程

为了方便沟通，我们把正在处理的节点称为关注节点

我们将父节点的父节点称为祖父节点

我们将父节点的兄弟节点成为叔叔节点

颜色依然沿用R表示红色，B表示黑色的方案

面对红黑树的插入迭代大致上有三种情况，相当于三种套路，只要掌握这三种套路就可以在插入数据之后生成一个合格的红黑树。

2.1 CASE1 如果关注节点是 a，它的叔叔节点 d 是红色，我们就依次执行下面的操作

1. 将关注的节点a的父节点b、叔叔节点d都设置为B
2. 将关注节点a的祖父节点c设置为R
3. 将关注节点设置为c
4. 根据情况跳转到CASE2或者CASE3
5. 注意如果这里的c节点是根节点,直接将c节点的颜色设置为B

是不是有点晕,我们画个图就好了

2.2 CASE2 如果关注节点是 a，它的叔叔节点 d 是黑色，关注节点 a 是其父节点 b 的右子节点

如果关注节点是 a，它的叔叔节点 d 是黑色，关注节点 a 是其父节点 b 的右子节点,我们就顺序执行如下操作：

1. 将关注节点的变为a的父节点b
2. 围绕b进行左旋
3. 跳转到CASE3

如图所示

CASE3 如果关注节点是a,他的叔叔节点d是黑色,而且关注节点a是其父节点b的左子节点

如果关注节点是 a，它的叔叔节点 d 是黑色，关注节点 a 是其父节点 b 的左子节点，我们就依次执行下面的操作：

1. 围绕关注节点a的祖父节点c右旋
2. 将关注节点a的父亲节点、叔叔节点的颜色对换
3. 完成

如图所示