我们前面讲了数组、链表等线性数据结构,今天我们来看一个非线性的数据结构--树。之前我们说所谓的线性数据结构是指数据就像一条线一样只有前和后两个方向。而树作为一种非线性的数据结构,肯定是不止这两个方向。
说起来其实树也只有一个前的方向,但是后就不一定是一个了。虽然部分树在极端情况下会退化成链表,但是大多数情况下,他都不只有一个“后”。
什么是树?
树的基本概念
维基百科中对树的解释是这样的:
在计算机科学中,树(英语:tree)是一种抽象数据类型(ADT)或是实现这种抽象数据类型的数据结构,用来模拟具有树状结构性质的数据集合。它是由n(n>0)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
- 每个节点都只有有限个子节点或无子节点;
- 没有父节点的节点称为根节点;
- 每一个非根节点有且只有一个父节点;
- 除了根节点外,每个子节点可以分为多个不相交的子树;
- 树里面没有环路(cycle)
不知道大家看明白了吗?我引用一张图:
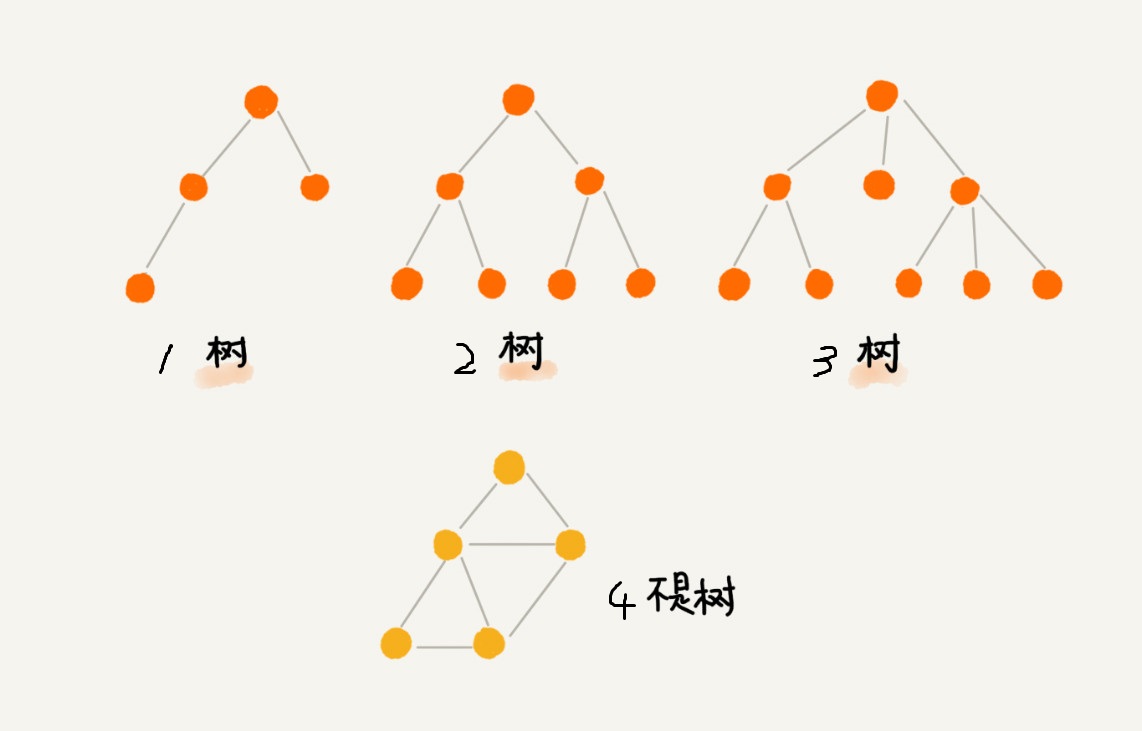
(该图片转自极客时间)
上图中,其中前面三个都是树,最后一个不是树。
名词解释
我们再结合一张图来简单解释一下树的几个名词,方便我们后续理解:
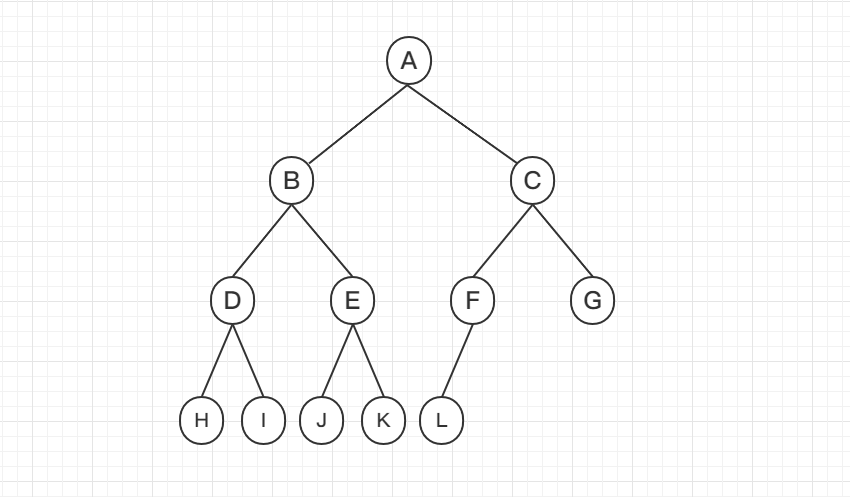
在这幅图中,通过观察我们可以得知这么几个属性:
父节点:A节点就是B节点的父节点,B节点是A节点的子节点
兄弟节点:B、C这两个节点的父节点是同一个节点,所以他们互称为兄弟节点
根节点:A节点没有父节点,我们把没有父节点的节点叫做根节点
叶子节点:图中的H、I、J、K、L节点没有子节点,我们把没有子节点的节点叫做叶子节点
节点的高度:节点到叶子结点的最长路径,比如C节点的高度是2(L->F是1,F->C是2)
节点的深度:节点到根节点的所经历的边的个数比如C节点的高度是1(A->C,只有一条边,所以深度=1)
节点的层:节点的深度+1
树的高度:根节点的高度
什么是二叉树?
树结构多种多样,但是我们在实际开发过程中直接用到或者间接用到的最常见的树就是二叉树。二叉树顾名思义,每个节点最多有两个子节点,我们分别将其称为左子节点、右子节点。不过我们并不要求二叉树上的每个节点都必须要有这两个节点,可以只有左子节点也可以只有右子节点。
完全二叉树
如果一个二叉树中,叶子节点全都在最后两层,最后一层的叶子节点全部都是靠左排列的,而且除了最后一层中,其他节点个数都要达到最大,这种二叉树叫做完全二叉树。这种理论调调可能看起来比较复杂,我们可以通过画图的方式快速理解,如图所示,这就是一个完全二叉树:
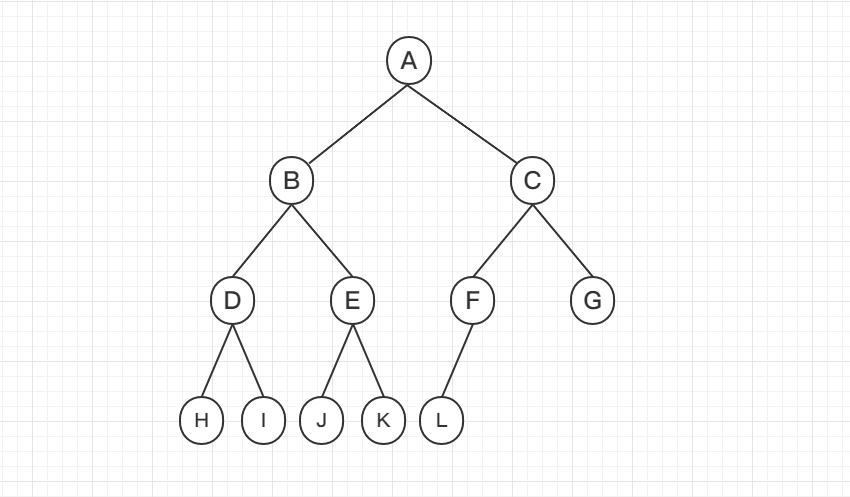
满二叉树
如果一个二叉树中,叶子节点全都在最底层,除了叶子节点之外,每个节点都有左右两个子节点,这种二叉树就是满二叉树。
如图所示,这就是一个满二叉树:
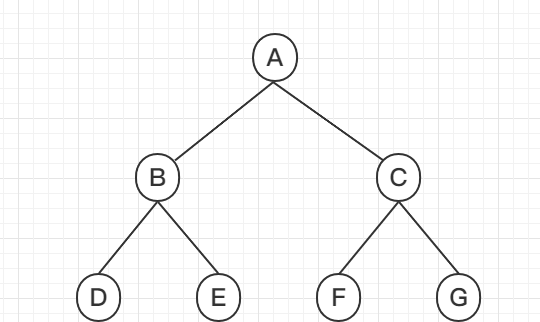
普通二叉树
除了刚才说的这两种特殊的二叉树之外的其他二叉树都是普通二叉树
二叉树的遍历
刚才我们简单梳理了一下二叉树的基本定义,那我们现在来看二叉树中非常重要的一个操作,二叉树的遍历。经典的方法有三种,前序遍历、中序遍历和后序遍历。其中,前、中、后序,表示的是节点与它的左右子树节点遍历打印的先后顺序。为了方便大家理解,我这里拿一张图,结合我们的遍历顺序要求,说一下输出结果应该是什么。大家可以借助结果来理解这个遍历顺序。

前序遍历
前序遍历是指,对于树中的任意节点来说,先打印这个节点,然后再打印它的左子树,最后打印它的右子树。
结合上图来说,前序遍历的输出结果是:
A -> B -> D -> H -> I -> E -> J -> K -> C -> F -> L -> G
中序遍历
中序遍历是指,对于树中的任意节点来说,先打印它的左子树,然后再打印它本身,最后打印它的右子树。
结合上图来说,中序遍历的输出结果是:
H -> D -> I -> B -> J -> E -> K -> A -> L -> F -> C -> G
后序遍历
后序遍历是指,对于树中的任意节点来说,先打印它的左子树,然后再打印它的右子树,最后打印这个节点本身。
结合上图来说,后续遍历的输出结果是:
H -> I -> D -> J -> K -> E -> B -> L -> F -> G -> C -> A
在最后,我把我创建的树的结构以及前中后序遍历的代码贴出来,大家看看和大家想象的是否一致
// 二叉树类
private static class TreeNode{
String data;
// 左子节点
TreeNode left;
// 右子节点
TreeNode right;
}
/**
* 前序遍历
* @param treeNode 二叉树
*/
private static void preOrderByTree(TreeNode treeNode) {
if (treeNode == null) {
return;
}
System.out.print(treeNode.data + " -> ");
preOrderByTree(treeNode.left);
preOrderByTree(treeNode.right);
}
/**
* 中序遍历
* @param node treeNode 二叉树
*/
private static void inOrderTree(TreeNode node) {
if (node == null) {
return;
}
inOrderTree(node.left);
System.out.print(node.data + " -> ");
inOrderTree(node.right);
}
/**
* 后序遍历
* @param node 二叉树
*/
private static void behindOrderTree(TreeNode node) {
if (node == null) {
return;
}
behindOrderTree(node.left);
behindOrderTree(node.right);
System.out.print(node.data + " -> ");
}
常见面试题
按层遍历一个二叉树
使用树+队列的方式来实现。这里是利用队列的FIFO的特性来做的,我们依次按层将节点放入队列中去,然后输出出来,并且在输出的时候,将输出节点的左右子节点写入队列中
/**
* 二叉树的按层遍历
* @param node
*/
private static void levelOrder(Node node) {
ArrayDeque<Node> queue = new ArrayDeque<>();
queue.add(node);
while (!queue.isEmpty()) {
Node pollNode = queue.poll();
System.out.println(pollNode.data);
if (pollNode.left != null) {
queue.add(pollNode.left);
}
if (pollNode.right != null) {
queue.add(pollNode.right);
}
}
}