斯特林公式 ——Stirling公式（取N阶乘近似值)（转）

斯特灵公式是一条用来取n阶乘近似值的数学公式。一般来说，当n很大的时候，n阶乘的计算量十分大，所以斯特灵公式十分好用。从图中可以看出，即使在n很小的时候，斯特灵公式的取值已经十分准确。

                                                    

公式为：   

 从图中看出，对于足够大的整数n，这两个数互为近似值。更加精确地：   

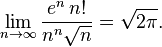             或者        

 

 这个公式，以及误差的估计，可以推导如下。我们不直接估计n!，而是考虑它的自然对数：

   

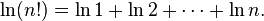
按一般方法计算N的阶乘，其时间复杂度为O（N）：    N！= 1 * 2 * 3 * 4 * 5 * ............ * N；

如果要计算N后得到的数字为几位数，则我们可以知道其位数等于lgN！+1；

则: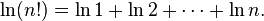 

但是当N很大的时候，我们可以通过斯特林公式进行优化：（即Stirling公式）

（e = 2.718）

斯特林公式可以用来估算某数的大小，结合lg可以估算某数的位数，或者可以估算某数的阶乘是另一个数的倍数。

例题：  http://acm.hdu.edu.cn/showproblem.php?pid=1018

题目给出的N的范围是: 1<= N <= 10⁷  

^{用普通方法肯定算不出N的阶乘后的出的数字位数，但运用斯特林公式则很好解决.}

 

 

Stirling 公式

即：

    Stirling公式的意义在于：当n足够大时，n!计算起来十分困难，虽然有很多关于n!的等式，但并不能很好地对阶乘结果进行估计，尤其是n很大之后，误差将会非常大。但利用Stirling公式可以将阶乘转化成幂函数，使得阶乘的结果得以更好的估计。而且n越大，估计得越准确。

 

利用Stirling公式求解n!的位数：易知整数n的位数为[lgn]+1。利用Stirling公式计算n!结果的位数时，可以两边取对数，得:

故n!的位数为：

 

url : https://blog.csdn.net/liangzhaoyang1/article/details/51145807#commentBox