树的遍历与递归

最近做一个统计工作，需要遍历一些文件，一个文件夹下面有很多层的小文件，如何算出这个文件夹下面有多少文件？相信很多人第一时间都能想到递归遍历，这是最直接，最简单的办法。在计算机中，函数调用是通过栈（stack）这种数据结构实现的，每当进入一个函数调用，栈就会加一层栈帧，每当函数返回，栈就会减一层栈帧。由于栈的大小不是无限的，所以，递归调用的次数过多，可能会导致栈溢出。当文件夹深度足够深，递归的反复调用会导致方法一直无法释放，造成jvm的栈溢出。那我们该怎么办？

如何遍历文件夹

学过数据结构的都知道，文件夹就类似于数据结构的中的树，遍历文件夹就如同遍历树。常见的遍历思想有深度优先遍历和广度优先遍历，其中递归遍历就属于深度优先遍历的一种。

一、递归遍历

public void traverseFile_recursion(File root) {
    if (root != null) {
        if (root.isDirectory()) {
            File[] files = root.listFiles();
            for (File f : files) {
                traverseFile_recursion(f);
            }
        } else {
            System.out.println(root.getPath());
        }
    }
}

递归方法遍历很容易看懂，递归函数的优点是定义简单，逻辑清晰。这里不细说了，看上面代码就OK了。

二、非递归的深度优先遍历

public void traverseFile_depth(File root) {
    Stack<File> fileStack = new Stack<>();
    File file;
    if (root != null && root.isDirectory()) {
        fileStack.push(root);
    }
    while (!fileStack.isEmpty()) {
        file = fileStack.pop();
        File[] files = file.listFiles();
        for (File f : files) {
            if (f.isDirectory()) {
                fileStack.push(f);
            } else {
                System.out.println(f.getPath());
            }
        }
    }
}

深度优先遍历，借助了一个栈，然后按次序读取文件夹的元素，并判断如果是文件夹则把该文件夹入栈。然后栈顶的文件夹再出栈，遍历，以此类推，直到所有的文件夹都出栈，再也没有文件夹入栈。

三、广度优先遍历

public void traverseFile_Width(File root) {
    Queue<File> fileQueue = new ArrayDeque<>();
    File file;
    if (root != null && root.isDirectory()) {
        fileQueue.add(root);
    }
    while (!fileQueue.isEmpty()) {
        file = fileQueue.remove();
        File[] files = file.listFiles();
        for (File f : files) {
            if (f.isDirectory()) {
                fileQueue.add(f);
            } else {
                System.out.println(f.getPath());
            }
        }
    }
}

广度优先遍历，借助了一个队列，然后按次序读取文件夹的元素，并判断如果是文件夹则把该文件夹加入队尾，然后队首的文件夹再出队，遍历，以此类推，直到所有的文件夹都出队，再也没有文件夹入队。

关于递归的性能问题

虽然递归方法在解决一些问题时，逻辑思路很清晰，在很多情况下递归还是不建议使用的，效率偏低，严重的情况下，会造成栈溢出。解决办法是使用尾递归或者使用循环方式。理论上，所有的递归函数都可以写成循环的方式，但循环的逻辑不如递归清晰。下面，举例子说明一下

一、斐波拉契数列

斐波拉契数列指的是这样一个数列：1、1、2、3、5、8、13、21、34、……第1个和第2个数是1，从第3个位置起，每个数等于它前面两个数的和。求第 n 个位置的数是多少？
使用递归方法实现很简单，方法如下：

public long fun1(int x) {
    if (x == 1)
        return 1;
    else if (x == 2)
        return 1;
    else {
        return fun1(x - 1) + fun1(x - 2);
    }
}

测试代码如下：

public static void main(String[] args) {
    long start_time = System.currentTimeMillis();
    long result = new Fibo().fun1(46);
    System.out.println("结果:  " + result);
    long end_time = System.currentTimeMillis();
    System.out.println("耗时： " + (end_time - start_time));
}

以下是基于我的PC（i7-7700,16G-DDR4-2400）的执行结果:
位置：46

结果:  1836311903
耗时： 5170

位置：47

结果:  2971215073
耗时： 8355

位置：48

结果:  4807526976
耗时： 13377

位置：49

结果:  7778742049
耗时： 21941

位置：50

结果:  12586269025
耗时： 34915

位置：51

结果:  20365011074
耗时： 57158

看这个时间增加，你还想用递归求吗？求位置51的用时接近一分钟。
下面用循环来实现：

public long fun2(int x) {
    long num1 = 1;
    long num2 = 1;
    long result = 0;
    if (x == 1) {
        return 1;
    } else if (x == 2) {
        return 1;
    } else {
        for (int i = 3; i <= x; i++) {
            result = num1 + num2;
            num1 = num2;
            num2 = result;
        }
        return result;
    }
}

同样测试位置 51 的结果：

结果:  20365011074
耗时： 0

几乎是秒算出结果。再看看100位置：

结果:  3736710778780434371
耗时： 1

同样几乎是秒出结果。这说明，用循环的方式，时间几乎是常数级的。若要用递归方式求100位置的，我想我可以让程序执行，然后去睡觉了。

二、遍历打印 List 元素

上面关于递归使用，由于迭代层次还没到一定级别，所以只能时间长，还没到栈溢出的地步，下面我们测试一下遍历上万元素的了 List ,来说明，上代码：

public static void printElement(Iterator<Integer> iterator) {
    if (!iterator.hasNext()) {
        return;
    } else {
        System.out.println(iterator.next());
        printElement(iterator);
    }
}

测试代码：

public static void main(String[] args) {
    List<Integer> list = new ArrayList();
    for (int i = 0; i < 20000; i++) {
        list.add(i);
    }
    long start_time = System.currentTimeMillis();
    printElement(list.iterator());
    long end_time = System.currentTimeMillis();
    System.out.println("耗时： " + (end_time - start_time));
}

我们用递归的方式遍历 List ,运行结果部分截图：

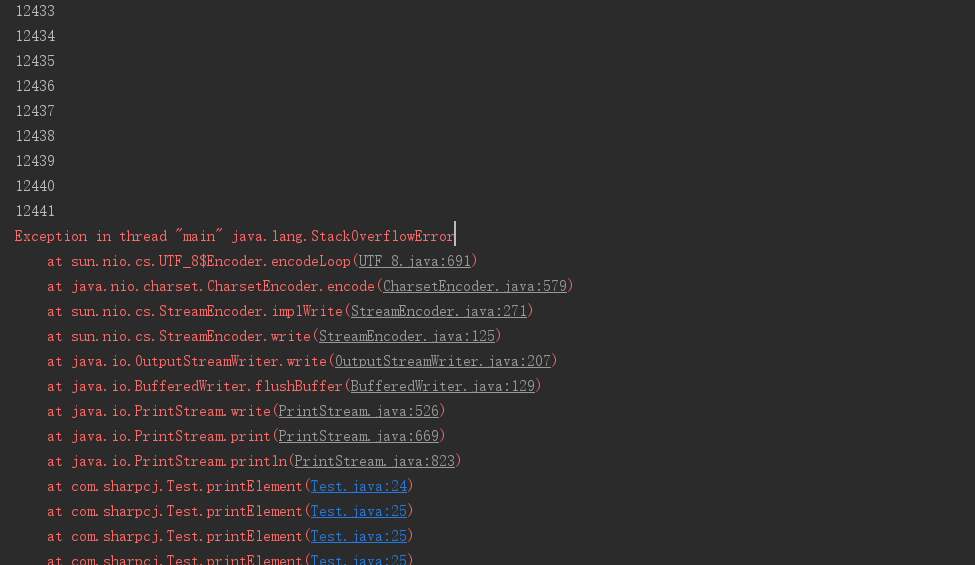
程序崩了，报的错，正是栈溢出。下面用循环方式遍历：

public static void printElement2(Iterator<Integer> iterator) {
    while (iterator.hasNext()) {
        System.out.println(iterator.next());
    }
}

测试结果部分截图如下：

方法调用时的内存情况

下面摘录《数据结构预算法分析-Java语言描述》中的几段话：
说明了方法调用的过程，由此也解释了深层次递归性能低的原因。

当调用一个新方法时，主调例程的所有局部变量需要由系统存储起来，否则被调用的新方法将会重写由主调例程的变量所使用的内存。不仅如此，该主调例程的当前位置也必须要存储，以便在新方法运行完后知道向哪里转移。这些变量一般由编译器指派给机器的寄存器，但存在某些冲突（通常所有的方法都是获取指定给1号寄存器的某些变量），特别是涉及到递归的时候。该问题类似于平衡符号的原因在于，方法调用和方法返回基本上类似于开括号和闭括号。

当存在方法调用的时候，需要存储的所有重要信息，诸如寄存器的值（对应变量的名字）和返回地址 （它可从程序计数器得到，一般情况是在一个寄存器中）等， 都要以抽象的方法存在“一张纸上”并被置于一个堆（pile）的顶部。然后控制转移到新方法，该方法自由地用它的一些值替代这些寄存器。如果它又进行其它的方法调用，那么它也遵循相同的过 程。当该方法要返回时，它查看堆顶部的那张“纸”并复原所有的寄存器，然后进行返回转移。

显然，所有全部工作均可由一个栈来完成，而这正是在实现递归的每一种程序设计语言中实际发生的事实。所储存的信息或称为活动记录（activation record），或叫做帧栈（stack frame）。

在实际计算机中的栈常常是从内存分区的高端向下增长，而在许多非Java系统中是不检测溢出的。失控递归可能导致栈溢出。