完全二叉树

 

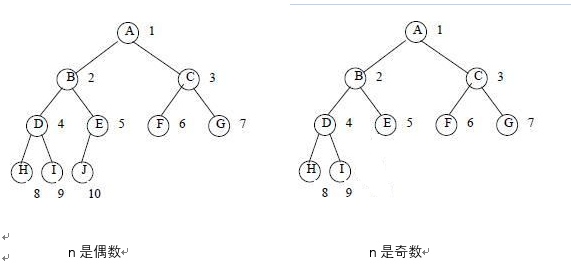
	n是偶数	n是奇数
i是叶子结点（i）无孩子	i>n/2	i>n/2
i有两个孩子	i<n/2	i<=n/2
i有1个孩子（且是左孩子）	i=n/2	无
i有左孩子	i<=n/2	i<=n/2
i有右孩子	i<n/2	i<=n/2
i有左兄弟	一定有	一定有
i有右兄弟	i+1 <= n	i+1 <= n  (一定有)

结点总数是n，最后一个有孩子的结点编号是：n/2，非叶子结点一定是n/2,叶子结点的个数是n – n/2.

深度为h的二叉树，除h层，1 to h-1 各层结点数目都达到最大，h层的结点都连续集中在最左边。这样的二叉树叫完全二叉树。

任意一个结点的左子树高度是L，它的右子树一定是L或L-1.

1 to h-2层的所有结点度都是2，h层的所有结点度都为0，h-1层的结点度可能为0,1,2。

叶子结点只可能出现在h和h-1层，只可能有1个或没有度为1的结点，若有，该结点的左孩子是二叉树最后一个结点。

二叉树要么没有孩子，个数是n-n/2，要么有两个孩子，个数是n/2或n/2-1,要么只有一个左孩子，且这样的结点仅有一个，如果一个结点有右孩子，必有左孩子。

n是偶数，有度为1的结点，n是奇数无度为1的结点。

i是奇数，必是右孩子，左兄弟是i-1,

i是偶数，必是左孩子，若n是奇数，必有右兄弟，是i+1；若n是偶数且i!=n,必有右兄弟，是i+1。

完全二叉树的两种形态

 

具有n个结点的完全二叉树的深度为k = [log2 n] +1 (自己推一遍)

深度为h的完全二叉树最多有  个结点(h>=1)， 最少有2^(h-1) – 1 + 1个结点；