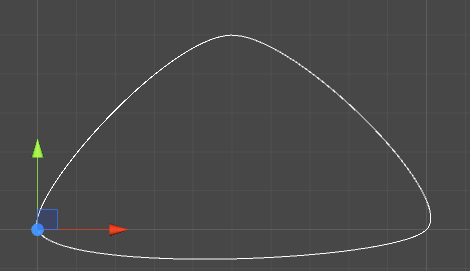
Hermite 曲线
已知曲线的两个端点坐标P0、P1,和端点处的切线R0、R1,确定的一条曲线。
参数方程
1. 几何形式
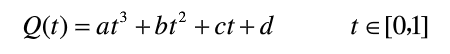
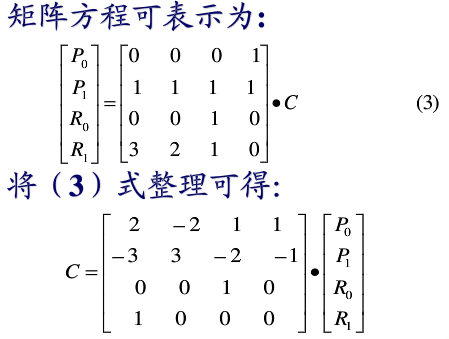
2. 矩阵形式
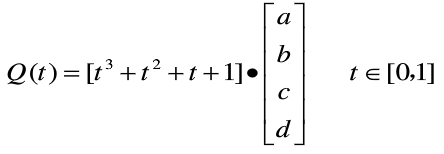
3. 推导
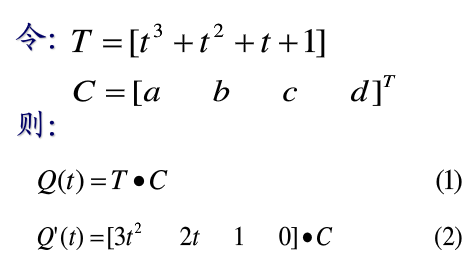




例子分析
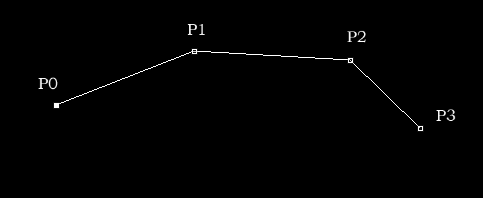
如上图有四个点,假如P0、P2是端点,那么向量R0=(P1-P0),R1=(P3-P2),将数据带入调和函数,即求得曲线。
在程序中,我们通常会使用特殊方法处理顶点之间的关系。
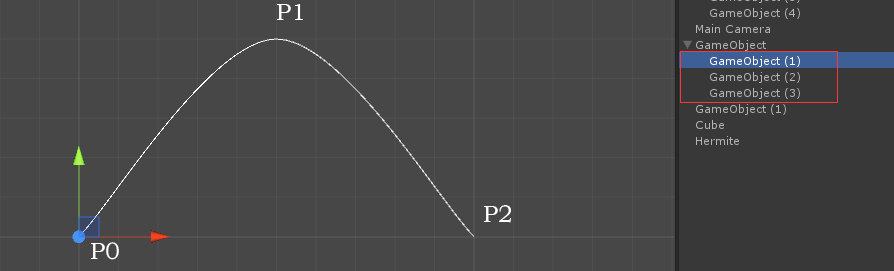
图中含有3个顶点,我们把每挨着的两个顶点看做是一条Hermite曲线,P0和P1是两个端点,那么现在,我们如何求得R1呢? 我们现在构建连个参考点F1,F2。
令 F1 = P0; F2 = P2;
那么 R1 = P1-F1; R2 = F2-P1;
然后将此值带入曲线函数,即可为求得的曲线。
程序代码
该代码是Unity脚本代码:
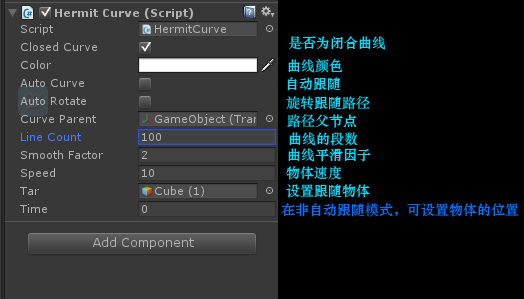
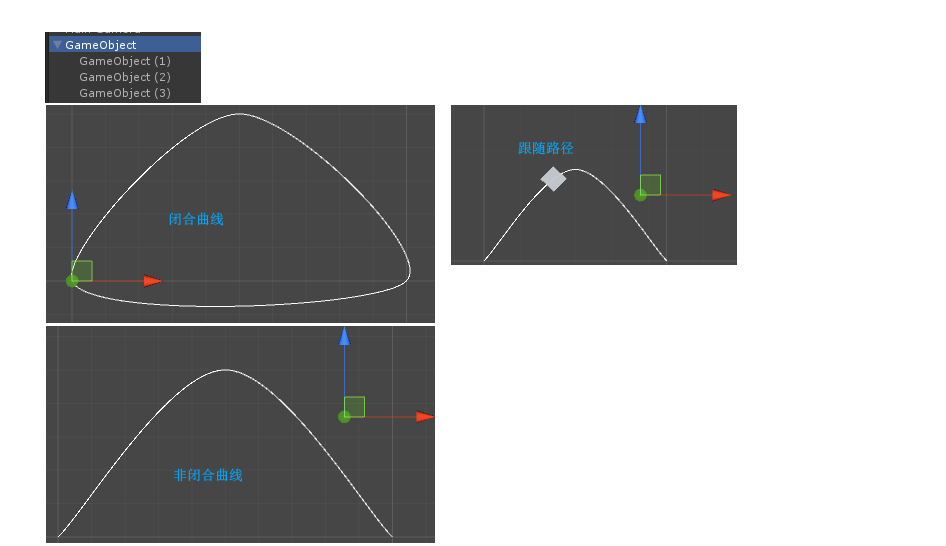
1. 实现编辑器闭合曲线和非闭合曲线的绘制;
2. 运行脚本,可以实现物体跟随曲线路径移动,可以勾选旋转跟随与不跟随;
3. 如果不进行自动跟随曲线路径,可以修改时间值,移动物体。

using UnityEngine; using System.Collections; using System.Collections.Generic; public class HermitCurve : Curve_Root { public Transform CurveParent; public int lineCount; private List<NodePath> nodePath; public float smoothFactor = 2.0f; private Transform[] transforms; private Vector3[] node; public float Speed = 10.0f; Vector3 curPos; Vector3 nextPos; Quaternion curRotate; Quaternion nextRotate; float moveTime; float curTime; public GameObject Tar; int index; private Transform T; public float time; /// <summary> /// 数据校正 /// </summary> void DadaCorrection() { //根节点验证 if (CurveParent == null) { Debug.LogError("Please add curve the root node."); return; } //修正平滑因子: 2时,较为理想。 smoothFactor = smoothFactor >= 10.0f ? 10.0f : smoothFactor; smoothFactor = smoothFactor <= 1.0f ? 1.0f : smoothFactor; } /// <summary> /// 计算路径节点 /// </summary> void ComputeNode() { //将节点添加入链表 Component[] mTrans = CurveParent.GetComponentsInChildren(typeof(Transform));//物体和子物体的Trans if (mTrans.Length - 1 < 2) { Debug.LogError("Please add at least two points."); return; } //非闭合曲线与闭合曲线的顶点时间计算:非闭合曲线,最后个顶点的时间为1.0,闭合曲线的最后个顶点的时间为倒数第二个顶点,因为他的最后个点是原点。 float t; if (closedCurve) { t = 1.0f / (mTrans.Length - 1); nodePath = new List<NodePath>(); for (int i = 1; i < mTrans.Length; i++)//根节点不参与路径节点的计算 { nodePath.Add(new NodePath(mTrans[i].transform.position, (i - 1) * t)); } //闭合曲线完整的节点 AddClosedCurveNode(); } else { t = 1.0f / (mTrans.Length - 2); nodePath = new List<NodePath>(); for (int i = 1; i < mTrans.Length; i++)//根节点不参与路径节点的计算 { nodePath.Add(new NodePath(mTrans[i].transform.position, (i - 1) * t)); } //非闭合曲线完整的节点 AddCurveNode(); } } // Use this for initialization void Start () { DadaCorrection(); ComputeNode(); node = new Vector3[lineCount+1]; //Vector3 start = nodePath[1].point; //Vector3 end; node[0] = nodePath[1].point; Vector3 end; //绘制节点 for (int i = 1; i <= lineCount; i++) { float ti = i / (float)lineCount; end = GetHermitAtTime(ti); if (node != null) { node[i] = end; } } T = new GameObject().transform; curPos = node[0]; nextPos = node[1]; moveTime = (nextPos - curPos).magnitude / Speed; Tar.transform.position = curPos; Tar.transform.transform.LookAt(nextPos); curRotate = Tar.transform.rotation; T.position = node[1]; T.LookAt(node[2]); nextRotate = T.rotation; curTime = 0; index = 1; } // Update is called once per frame void Update () { if (AutoCurve) { if (moveTime > curTime) { Tar.transform.position = Vector3.Lerp(curPos, nextPos, curTime / moveTime); if (AutoRotate) { Tar.transform.rotation = Quaternion.Slerp(curRotate, nextRotate, curTime / moveTime); } curTime += Time.deltaTime; } else { if (closedCurve) { index = ((index + 1) % (lineCount + 1) == 0) ? 0 : index + 1; } else { index = ((index + 1) % (lineCount+1) == 0) ? index : index + 1; } curPos = nextPos; nextPos = node[index]; curTime = 0; moveTime = (nextPos - curPos).magnitude / Speed; T.position = node[index]; curRotate = nextRotate; if (closedCurve) { int c1; if (index == node.Length-1) { c1 = 0; } else { c1 = index + 1; } T.LookAt(node[c1]); } else { int c1; if (index == node.Length - 1) { c1 = 0; } else { c1 = index + 1; T.LookAt(node[c1]); } } nextRotate = T.rotation; } } else { if (closedCurve) { if (AutoRotate) { time = time > 1.0f ? 0.0f : time; time = time < 0.0f ? 1.0f : time; Vector3 cur = GetHermitAtTime(time); Tar.transform.position = cur; float del = 1.0f / lineCount; Vector3 next0 = GetHermitAtTime(time + del); Tar.transform.LookAt(next0); } else { time = time > 1.0f ? 0.0f : time; time = time < 0.0f ? 1.0f : time; Vector3 cur = GetHermitAtTime(time); Tar.transform.position = cur; } } else { if (AutoRotate) { time = time > 1.0f ? 1.0f : time; time = time < 0.0f ? 0.0f : time; Vector3 cur = GetHermitAtTime(time); Tar.transform.position = cur; float del = 1.0f / lineCount; Vector3 next0 = GetHermitAtTime(time + del); Tar.transform.LookAt(next0); } else { time = time > 1.0f ? 1.0f : time; time = time < 0.0f ? 0.0f : time; Vector3 cur = GetHermitAtTime(time); Tar.transform.position = cur; } } } } /// <summary> /// 绘制曲线 /// </summary> void DrawCurve() { if (closedCurve) { Vector3 start = nodePath[1].point; Vector3 end; Gizmos.color = _Color; //绘制节点 for (int i = 1; i < lineCount; i++) { float time = i / (float)lineCount; end = GetHermitAtTime(time); //Debug.Log(end); Gizmos.DrawLine(start, end); start = end; } Gizmos.DrawLine(start, nodePath[nodePath.Count - 2].point); } else { Vector3 start = nodePath[1].point; Vector3 end; Gizmos.color = _Color; //绘制节点 for (int i = 1; i < lineCount; i++) { float time = i / (float)lineCount; end = GetHermitAtTime(time); //Debug.Log(end); Gizmos.DrawLine(start, end); start = end; } Gizmos.DrawLine(start, nodePath[nodePath.Count - 2].point); } } /// <summary> /// 在Scene场景中,绘制Hermite曲线 /// </summary> void OnDrawGizmos() { /*数据校正*/ DadaCorrection(); /*计算顶点*/ ComputeNode(); /*计算曲线*/ DrawCurve(); } /// <summary> /// 1. 非闭合曲线 /// </summary> public void AddCurveNode() { nodePath.Insert(0, nodePath[0]); nodePath.Add(nodePath[nodePath.Count - 1]); } /// <summary> /// 2. 闭合曲线 /// </summary> public void AddClosedCurveNode() { //nodePath.Insert(0, nodePath[0]); nodePath.Add(new NodePath(nodePath[0])); nodePath[nodePath.Count - 1].time = 1.0f; Vector3 vInitDir = (nodePath[1].point - nodePath[0].point).normalized; Vector3 vEndDir = (nodePath[nodePath.Count - 2].point - nodePath[nodePath.Count - 1].point).normalized; float firstLength = (nodePath[1].point - nodePath[0].point).magnitude; float lastLength = (nodePath[nodePath.Count - 2].point - nodePath[nodePath.Count - 1].point).magnitude; NodePath firstNode = new NodePath(nodePath[0]); firstNode.point = nodePath[0].point + vEndDir * firstLength; NodePath lastNode = new NodePath(nodePath[nodePath.Count - 1]); lastNode.point = nodePath[0].point + vInitDir * lastLength; nodePath.Insert(0, firstNode); nodePath.Add(lastNode); } /// <summary> /// 通过节点段数的时间大小,获取每段节点 /// </summary> /// <param name="t"></param> /// <returns></returns> public Vector3 GetHermitAtTime(float t) { //Debug.Log(t); int k; //最后一个顶点 if (t >= nodePath[nodePath.Count - 2].time) { return nodePath[nodePath.Count - 2].point; } for (k = 1; k < nodePath.Count-2; k++) { if (nodePath[k].time > t) break; } k = k - 1; float param = (t - nodePath[k].time) / (nodePath[k+1].time - nodePath[k].time); return GetHermitNode(k, param); } /// <summary> /// Herimite曲线:获取节点 /// </summary> /// <param name="index">节点最近的顶点</param> /// <param name="t"></param> /// <returns></returns> public Vector3 GetHermitNode(int index,float t) { Vector3 v; Vector3 P0 = nodePath[index - 1].point; Vector3 P1 = nodePath[index].point; Vector3 P2 = nodePath[index + 1].point; Vector3 P3 = nodePath[index + 2].point; //调和函数 float h1 = 2 * t * t * t - 3 * t * t + 1; float h2 = -2 * t * t * t + 3 * t * t; float h3 = t * t * t - 2 * t * t + t; float h4 = t * t * t - t * t; v = h1 * P1 + h2 * P2 + h3 * (P2 - P0) / smoothFactor + h4 * (P3 - P1) / smoothFactor; //Debug.Log(index + " "+ t+" "+v); return v; } } /// <summary> /// 节点类 /// </summary> public class NodePath { public Vector3 point; public float time; public NodePath(Vector3 v,float t) { point = v; time = t; } public NodePath(NodePath n) { point = n.point; time = n.time; } }
基类代码

using UnityEngine; using System.Collections; public class Curve_Root : MonoBehaviour { //曲线是否为闭合曲线 public bool closedCurve = false; //曲线的颜色 public Color _Color = Color.white; //自动跟随路径 public bool AutoCurve = false; //旋转跟随 public bool AutoRotate = false; }
路径漫游
在曲线函数中,参数t取值[0,1],将曲线进行分段。那么能够计算出每一个点的位置。因此,在路径漫游中,我们从原点出发,将t的增量作为下一个点位置,进行插值移动。就实现了路径漫游,同时进行朝向下一个顶点旋转,就可以使看的方向随着曲线变化。
Unity 3D 项目工程
http://download.csdn.net/detail/familycsd000/9365859