BoW模型最初应用于文本处理领域,用来对文档进行分类和识别。BoW 模型因为其简单有效的优点而得到了广泛的应用。其基本原理可以用以下例子来给予描述。给定两句简单的文档:
文档 1:“我喜欢跳舞,小明也喜欢。”
文档 2:“我也喜欢唱歌。”
基于以上这两个文档,便可以构造一个由文档中的关键词组成的词典:
词典={1:“我”,2:“喜欢”,3:“跳舞”,4:“小明”,5:“也”,6:“唱歌”}
这个词典一共包含6个不同的词语,利用词典的索引号,上面两个文档每一个都可以用一个6维向量表示(用整数数字0~n(n为正整数)表示某个单词在文档中出现的次数。这样,根据各个文档中关键词出现的次数,便可以将上述两个文档分别表示成向量的形式:
文档 1:[1, 2, 1, 1, 1, 0]
文档 2:[1, 1, 0, 0, 1, 1]
从上述的表示中,可以很清楚地看出来,在文档表示过程中并没有考虑关键词的顺序,而是仅仅将文档看成是一些关键词出现的概率的集合(这是Bag-of-words模型的缺点之一),每个关键词之间是相互独立的,这样每个文档可以表示成关键词出现频率的统计集合,类似于直方图的统计表示。
Bag-of-words模型在计算机视觉的应用
SIFT特征虽然也能描述一幅图像,但是每个SIFT矢量都是128维的,而且一幅图像通常都包含成百上千个SIFT矢量,在进行相似度计算时,这个计算量是非常大的,通行的做法是用聚类算法对这些矢量数据进行聚类,然后用聚类中的一个簇代表BOW中的一个视觉词,将同一幅图像的SIFT矢量映射到视觉词序列生成码本,这样每一幅图像只用一个码本矢量来描述,这样计算相似度时效率就大大提高了。
计算机视觉领域的研究者们尝试将同样的思想应用到图像处理和识别领域,建立了由文本处理技术向图像领域的过渡。将文本分类问题与图像分类问题相比较,会发现这样的问题,对于文本来讲,文本是由单词组成的,因此提取关键词的过程也是顺理成章,没有任何歧义或者限制。但对于图像来讲,如何定义图像的“单词”,则是需要首先解决的问题之一。研究者们通过对 BoW 模型进行研究和探索,提出了采用k -means 聚类方法对所提取的大量特征进行无监督聚类,将具有相似性较强的特征归入到一个聚类类别里,定义每个聚类的中心即为图像的“单词”,聚类类别的数量即为整个视觉词典的大小。这样,每个图像就可以由一系列具有代表性的视觉单词来表示,如图1所示。
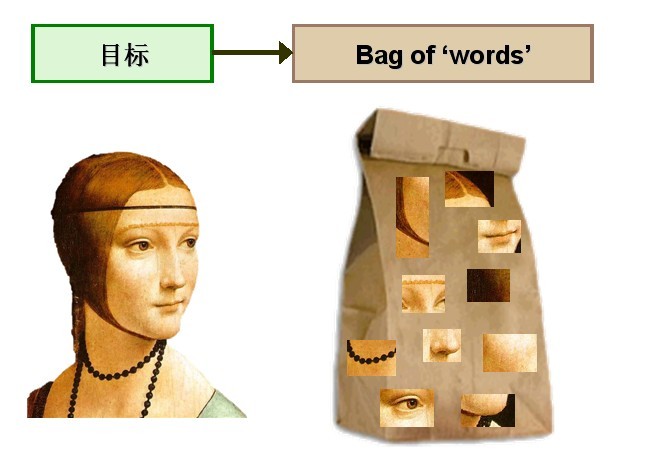
图1
在得到每类图像的视觉单词袋表示之后,便可以应用这些视觉单词来构造视觉词典,然后对待分类图像进行同样方法的特征提取和描述,最后将这些特征对应到视觉词典库中进行匹配,去寻找每个特征所对应的最相似的视觉单词,得到直方图统计表示,然后应用分类器进行分类。这样就将应用于文档处理的BoW模型思想成功地移植到了图像处理领域。斯坦福大学的 Li Feifei 等人在此方面做出了突出的贡献。
在应用BoW模型来表述图像时,图像被看作是文档,而图像中的关键特征被看作为“单词”,其应用于图像分类时主要包括三个步骤:
- 特征提取和描述;
- 视觉词典构造;
- 单词表的中词汇表示图像
Step1:图像特征提取和描述
特征提取和描述的主要任务是从图像中抽取具有代表性的局部特征。要求这些特征具有较强的可区分性,能最大限度地与其他物体进行区分。此外,还要求被提取的特征具有较好的稳定性,此类特征经常存在于图像的高对比度区域,例如物体边缘与角点。
BoW模型中的一些典型图像特征的提取和描述方法
(1) 规则网格(Regular Grid)方法是特征提取的最简单且有效的方法之一,该方法将图像应用均匀网格进行划分,从而得到一些图像的局部区域特征,此方法在应用于自然场景分类时收到了良好的效果。图2给出了利用规则网格方法得到的特征提取结果。
图2
采用规则网格法的优点在于:(1)可以人为地设定网格的划分级别,得到想要的特征数目;(2)在划分过程中可以对一些特征进行精确的定位;(3)可以充分利用图像的数据信息,最大限度的做到信息的完整性。然而该方法也存在一定的缺点,例如引入了大量的冗余(背景)信息,而降低了对象本身所提供的有用信息的价值。
(2) 兴趣点检测方法;兴趣点检测子和兴趣区域检测子的实现方法都是通过数学计算,去抽取满足一定数学条件的特征点或者区域,常用的检测子有edge-laplace、harris-laplace、hessian-laplace、harris-affine、hessian-affine、MSER、salient regions实际上,针对具体任务不同以及应用的数据库不同,最佳检测子的选择也很不相同。Step2:构建视觉词典
利用聚类算法(如:K-Means算法)对步骤1提取的特征描述子构造单词表(词典),特征描述子分为K个簇,以使簇内具有较高的相似度,而簇间相似度较低,将词义相近的词汇合并,作为单词表中的基础词汇,聚类类别的数量K即为整个视觉词典的大小基础词汇的个数。
Step3:单词表的中词汇表示图像
从每幅图像中提取很多个特征点,这些特征点都可以用单词表中的单词近似代替,通过统计单词表中每个单词在图像中出现的次数,可以将图像表示成为一个K维数值向量。
为什么要用BOW模型描述图像
SIFT特征虽然也能描述一幅图像,但是每个SIFT矢量都是128维的,而且一幅图像通常都包含成百上千个SIFT矢量,在进行相似度计算时,这个计算量是非常大的,通行的做法是用聚类算法对这些矢量数据进行聚类,然后用聚类中的一个簇代表BOW中的一个视觉词,将同一幅图像的SIFT矢量映射到视觉词序列生成码本,这样每一幅图像只用一个码本矢量来描述,这样计算相似度时效率就大大提高了。构建BOW码本步骤:
1. 假设训练集有M幅图像,对训练图象集进行预处理。包括图像增强,分割,图像统一格式,统一规格等等。2、提取SIFT特征。对每一幅图像提取SIFT特征(每一幅图像提取多少个SIFT特征不定)。每一个SIFT特征用一个128维的描述子矢量表示,假设M幅图像共提取出N个SIFT特征。3. 用K-means对2中提取的N个SIFT特征进行聚类,K-Means算法是一种基于样本间相似性度量的间接聚类方法,此算法以K为参数,把N个对象分为K个簇,以使簇内具有较高的相似度,而簇间相似度较低。聚类中心有k个(在BOW模型中聚类中心我们称它们为视觉词),码本的长度也就为k,计算每一幅图像的每一个SIFT特征到这k个视觉词的距离,并将其映射到距离最近的视觉词中(即将该视觉词的对应词频+1)。完成这一步后,每一幅图像就变成了一个与视觉词序列相对应的词频矢量。
设视觉词序列为{眼睛 鼻子 嘴}(k=3),则训练集中的图像变为:
第一幅图像:[1 0 0]
第二幅图像:[5 3 4]......
2. 构造码本。码本矢量归一化因为每一幅图像的SIFT特征个数不定,所以需要归一化。如上述例子,归一化后为[1 0 0],1/12*[5 3 4].测试图像也需经过预处理,提取SIFT特征,将这些特征映射到为码本矢量,码本矢量归一化,最后计算其与训练码本的距离,对应最近距离的训练图像认为与测试图像匹配。
当然,在提取sift特征的时候,可以将图像打成很多小的patch,然后对每个patch提取SIFT特征。
总结一下,整个过程其实就做了三件事,首先提取对 n 幅图像分别提取SIFT特征,然后对提取的整个SIFT特征进行k-means聚类得到 k 个聚类中心作为视觉单词表,最后对每幅图像以单词表为规范对该幅图像的每一个SIFT特征点计算它与单词表中每个单词的距离,最近的+1,便可得到该幅图像的码本。实际上第三步是一个统计的过程,所以BOW中向量元素都是非负的。Yunchao Gong 2012年NIPS上有一篇用二进制编码用于图像快速检索的文章就是针对这类元素是非负的特征而设计的编码方案。
未完待续。。。
参考文献:
[1]王莹.基于BoW模型的图像分类方法研究
[2]https://en.wikipedia.org/wiki/Bag-of-words_model_in_computer_vision
[3]网络资源:SIFT算法的应用--目标识别之Bag-of-words模型
SIFT特征虽然也能描述一幅图像,但是每个SIFT矢量都是128维的,而且一幅图像通常都包含成百上千个SIFT矢量,在进行相似度计算时,这个计算量是非常大的,通行的做法是用聚类算法对这些矢量数据进行聚类,然后用聚类中的一个簇代表BOW中的一个视觉词,将同一幅图像的SIFT矢量映射到视觉词序列生成码本,这样每一幅图像只用一个码本矢量来描述,这样计算相似度时效率就大大提高了。
