数据结构——线段树

前置知识

二叉树

正篇

首先先来一个问题：给出一个长度为n的序列和m个操作，操作分别是:

1. 单点修改
2. 单点查询
3. 区间加减
4. 区间查询和

模板题出处

最简单的做法就是在数组上暴力for, 这样的话单点修改和查询的时间复杂度是(O(1)), 区间加减和区间查询的复杂度是(O(n)), 这样写的话简单是简单，但是会出现这样的情况：

(纯暴力居然还有70？？？我还以为只有30呢)

如图所示，就会T飞。

那么我们怎么才能加速这一过程呢，答案就是线段树

线段树可以用来维护区间信息，例如区间和，RMQ等，更进一步还有权值线段树和可持久化线段树(还有重口味线段树)......是一种用处比较多的数据结构，但是要注意，有些区间问题线段树是无法解决的，比如说区间众数。

emmm......鬼扯这么多，先来看一下线段树的基本结构吧。

线段树首先是一颗二叉树，每一个节点维护的是一个区间的信息。比如说根节点维护的是[1,n]，然后叶子节点维护的是[x,x]。并且线段树用的是二分的思想，也就是说对于一个维护信息([l,r])的节点，它的两个子节点分别维护的是 ([l,frac{l+r}{2}])和([frac{l+r}{2}+1,r])，给一张图可以更加清晰地看出这种结构：

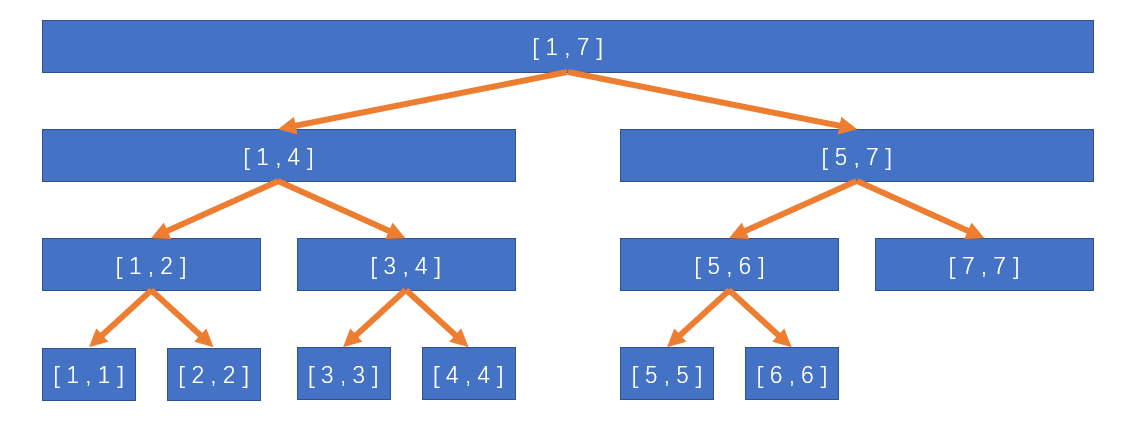
从图中可以很清晰地看出，实际上就是用一些线段去覆盖一个区间，线段树也因此得名

那么，我们该怎么写线段树呢？

首先，我们需要做一些准备工作：

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=200010;
struct node{
	ll sum,tag;
}t[maxn<<2];//线段树
ll arr[maxn];//原数组

这里的空间必须要开大一点，并且还用用long long

结构体里面的tag暂时不用管，以后再说具体有什么用

接着，我们写一个维护节点的函数，实际上就是把子节点的值传递到父节点里面去：

void update(ll pos){
	t[pos].sum=t[pos<<1].sum+t[pos<<1|1].sum;
}

然后就开始build(建树)函数了：

void build(ll l,ll r,ll pos){
	if(l==r){
		t[pos].sum=arr[l];
		return;
	}
	ll mid=(l+r)/2;
	build(l,mid,pos<<1);
	build(mid+1,r,pos<<1|1);
	update(pos);
}

这里面的 l 和 r 分别对应的是二分的过程中需要的左右区间，pos，对应的是在树里面的编号。

当l==r的时候，就是递归到叶子节点的时候，此时我们直接填数字

否则取一个mid值然后接着递归

因为我们知道，对于一棵二叉树来讲，非叶节点n的左儿子的编号是(2n),右节点的编号是(2n+1)，所以我们可以很快地写出递归的调用

要注意的是，在递归返回的时候要用上面写的update函数去维护区间和

建树完成后相对应的就是查询了。查询分为单点查询和区间查询，但是我们可以发现，单点查询其实就是查询区间 [ x , x ] ，所以我们只用写一个区间查询的就好了

区间查询本质上就是对在原数组上的区间 [ l , r ],在线段树上找 l 和 r 分别对应的点。这里我们使用二分法来寻找。

就这上面的那个图来看，如果我们只是查找 [ 5 , 7 ]或者 [ 1 , 4 ]那还好，但是如果我们查找的是[ 4 , 6 ]这种区间的话该怎么办呢？

其实我们可以在二分的过程中把[ 4 , 6 ]拆成[ 4 , 4 ]和[ 5 , 6 ]，然后直接统计和就好了。

感觉直接看代码会直接一点：

ll query(ll tl,ll tr,ll l,ll r,ll pos){
	if(tl<=l&&tr>=r){
		return t[pos].sum;
	}
	if(tl>r||tr<l) return 0;
	ll mid=(l+r)/2;
	//pushdown(l,r,pos);
    //这里的pushdown就当不存在哈...以后会解释的
	return query(tl,tr,l,mid,pos<<1)+query(tl,tr,mid+1,r,pos<<1|1);
}

tl和tr是查寻区间，l和r是我们要二分的区间，pos对应的是线段树内部的位置

很明显，如果tl<=l&&tr>=r的时候，就代表着此时我们的二分到的区间是在查询区间内部的，那么我们就没必要继续二分下去了，可以直接返回。

否则的话，就看看我们二分到的区间是不是完全不在查询区间内部，比如说这种情况：

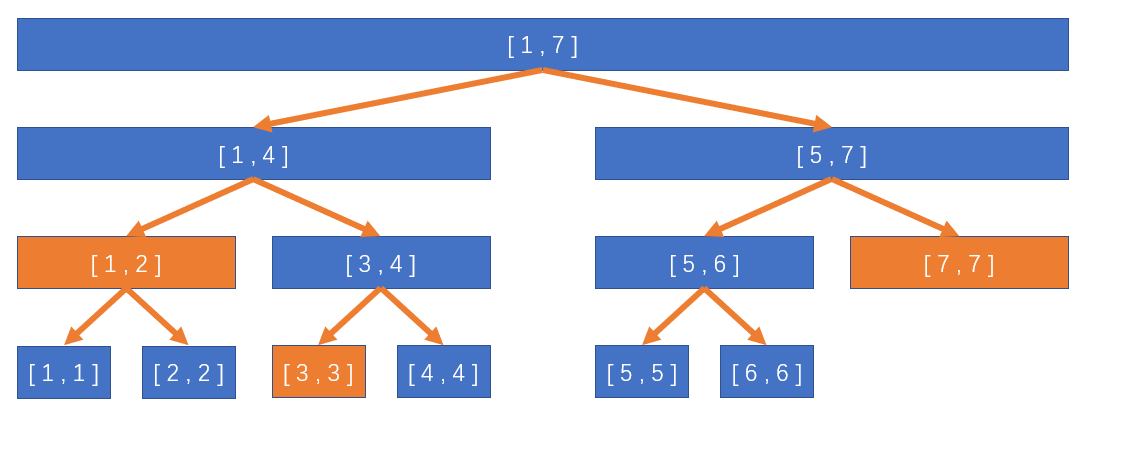
还是查询 [ 4 , 6 ]，所以我们在二分的过程中会出现途中黄(橙?)色的区间，但是这些区间都不会对答案有所贡献，也就是说完全在查询区间外(和插查询区间没有交集)，这个时候我们也没必要沿着它们继续二分了，直接返回0就好了

最后把搞出来的区间答案合并一下返回就没了

区间修改

由于线段树每一个节点都是维护的区间信息，所以如果我们只是简单地用单点查询的思路去修改，时间复杂度就会飙到(O(nlogn)),很明显连数组都不如，那么为了加速这一过程，我们会使用一个技巧——懒惰标记(lazy_tag)

懒惰和懒惰标记

懒惰的本质就是：

打个比方。我们区间查询的时候会发现，如果我们二分到某一个区间内，发现这个区间被查询区间完全覆盖了，此时我们是直接返回的，并没有继续二分下去，因为继续二分是没必要的。同样的，我们如果也是对这一个区间进行区间加的话，我们其实可以用(O(1))的时间内算出整个区间在区间加之后的区间和，就是sum=sum+(r-l+1)*v;，那么我们极端一点想，如果对于以后的所有查询，这个区间都是被完全覆盖在查询区间内的话(也就是说每次程序跑到这里都会直接返回)，那么我们为什么要在区间加的时候在这个区间底下继续二分呢？这就是懒惰（惰性）操作的一个基本的概念。

但是事事没法像我们假设的那样如此极端，同样，某一个区间总会在某一次询问的时候被残忍地分割开来。此时就出问题了，我们当初没有对这个区间底下的子节点进行真正意义上的加减，那么我们还怎么获得正确的答案呢？答案就是继续懒惰。简单来讲就是query查到哪里我们就懒到哪里，query如果继续在这个区间内二分的话我们就继续更新其对应的区间，query在哪里停下我们就在那里停下，绝对不会更新多余的节点。

给一张图看一下吧：

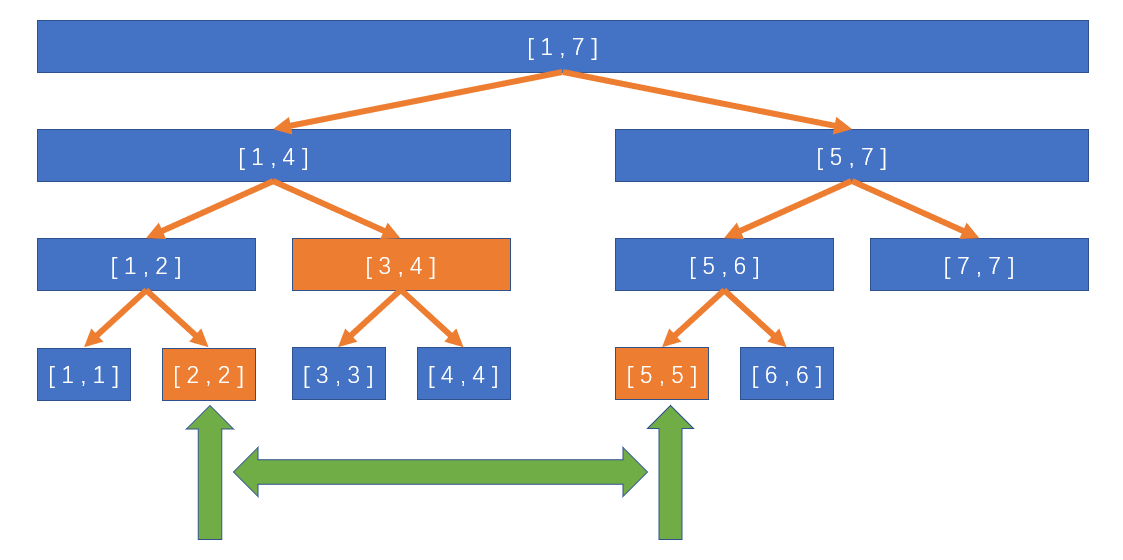
假如我们要区间加的是如图所示的绿色区间，我们只用给两边的 [ 2 , 2 ] 和 [ 5 , 5 ]分别+v，然后给 [ 3 , 4 ]加上(4-3+1)*v就好了。

如果我们查询 [ 2 , 4 ]的时候我们也不需要管 [ 3 , 3 ] 和 [ 4 , 4 ] 是不是被更新到了，因为反正 [ 3 , 4 ] 是被更新了的，那就直接拿来和 [ 2 , 4 ]合并一下就好了

如果以后我们要查询 [ 4 , 6 ]的话我们就先把 [ 3 , 4 ] 懒惰的结果给传下来用来更新 [ 3 , 3 ] 和 [ 4 , 4 ]，然后接下来就是一个简单地查询了

那我们该怎么更新 [ 3 , 4 ] 的子节点呢？这个时候就是要用到懒惰标记了。

懒惰标记(就是结构体里面的tag)记录的是从程序开始到此时query的时候区间内部发生的变化，可以理解为delta。打个比方，一开始build的时候tag都是0，因为此时就是初始状态。当对区间 [ l , r ] 区间+v(这里假设 [ l , r ] 是线段树内一个节点对应的区间)，[ l , r ] 的tag就会+(r-l+1)*v，同样适用于其他节点。

那么怎么才能懒下去呢？我们可以这么想，如果区间([l,r])都+v了的话，那么区间 ([l,frac{l+r}{2}])和([frac{l+r}{2}+1,r])肯定是一样的。我们直接把v给下推到这两个区间内就好了。

放一下代码：

void f(ll pos,ll l,ll r,ll k)
{
    t[pos].tag=t[pos].tag+k;
    t[pos].sum=t[pos].sum+k*(r-l+1);
}
void pushdown(ll l,ll r,ll pos){
	if(!t[pos].tag) return;
	ll mid=(l+r)/2;
	f(pos<<1,l,mid,t[pos].tag);
	f(pos<<1|1,mid+1,r,t[pos].tag);
	t[pos].tag=0;
}

个人觉得还是很好理解的。

这里要注意，由于pushdown是一个自上而下的过程，所以我们要在query和add的时候优先pushdown，否则的话就会更新错一些信息

模板题AC代码：

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=200010;
struct node{
	ll sum,tag;
}t[maxn<<2];
ll arr[maxn];
void update(ll pos){
	t[pos].sum=t[pos<<1].sum+t[pos<<1|1].sum;
}
void build(ll l,ll r,ll pos){
	if(l==r){
		t[pos].sum=arr[l];
		return;
	}
	ll mid=(l+r)/2;
	build(l,mid,pos<<1);
	build(mid+1,r,pos<<1|1);
	update(pos);
}
void f(ll pos,ll l,ll r,ll k)
{
    t[pos].tag=t[pos].tag+k;
    t[pos].sum=t[pos].sum+k*(r-l+1);
}
void pushdown(ll l,ll r,ll pos){
	if(!t[pos].tag) return;
	ll mid=(l+r)/2;
	f(pos<<1,l,mid,t[pos].tag);
	f(pos<<1|1,mid+1,r,t[pos].tag);
	t[pos].tag=0;
}
void add(ll tl,ll tr,ll l,ll r,ll v,ll pos){
	if(tl<=l&&tr>=r){
		t[pos].sum+=v*(r-l+1);
		t[pos].tag+=v;
		return;
	}
	if(r<tl||l>tr){
		return;
	}
	ll mid=(l+r)/2;
	pushdown(l,r,pos);
	add(tl,tr,l,mid,v,pos<<1);
	add(tl,tr,mid+1,r,v,pos<<1|1);
	update(pos);
}
ll query(ll tl,ll tr,ll l,ll r,ll pos){
	if(tl<=l&&tr>=r){
		return t[pos].sum;
	}
	if(tl>r||tr<l) return 0;
	ll mid=(l+r)/2;
	pushdown(l,r,pos);
	return query(tl,tr,l,mid,pos<<1)+query(tl,tr,mid+1,r,pos<<1|1);
}
int main(void){
	ios::sync_with_stdio(false);
	ll n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>arr[i];
	}
	build(1,n,1);
	for(int i=1;i<=m;i++){
		ll opt,x,y,k;
		cin>>opt;
		if(opt==1){
			cin>>x>>y>>k;
			add(x,y,1,n,k,1);
		}else{
			cin>>x>>y;
			cout<<query(x,y,1,n,1)<<endl;
		}
	}
}

这就是线段树最基本的思想。线段树有很多种形式和用处，这里只讲一下最基本的用处

emmm......推荐看一下这道题：线段树模板2

就是要注意维护两个lazy_tag的时候传递的顺序和取模，剩下的和原来一样

代码就不放了