一、OpenCV中的轮廓
在OpenCV中，将 Canny 等边缘检测算法根据像素间的差异检测出轮廓边界的像素，作为一个整体来研究和分析，称之为轮廓。比如对于这副图片：
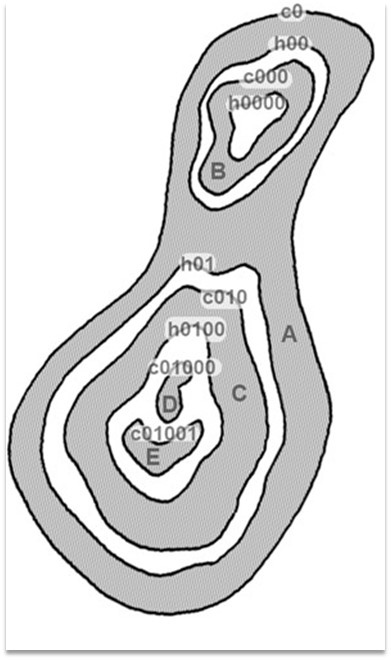
图像的上半部分是一张白色背景上的测试图像，包含了一系列标记 A 到 E的区域。寻找到的轮廓被标记为 cX 或 hX， 其中c 代表 “轮廓（contour）”，h 代表 “孔（hole）”（也可以理解为内轮廓）。
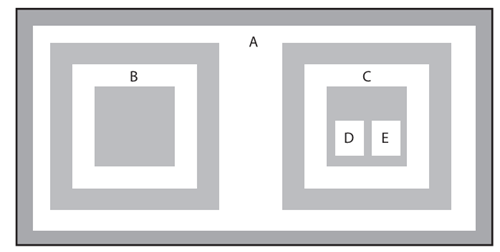
同样，左图是原始图片，右图是寻找到的轮廓，它也采用了类似的标注方法。
二、函数调用细节
寻找轮廓的主要函数是 cv::findContours()，它的主要定义为：
void cv::findContours(
cv::InputOutputArray image, // 输入图像，特别需要注意是二值图像
cv::OutputArrayOfArrays contours, //输出结果
cv::OutputArray hierarchy, // 层级结果
int mode, //定义轮廓是如何提取
int method, // 定义轮廓的寻找方法
cv::Point offset = cv::Point() // Offset every point
);其中参数定义：
参数一：输入图像，8位单通道；
参数二：“an array of arrays”，一般采用“ an STL vector of STL vectors”，找到的轮廓、函数调用后的运算结果保存在这里；
参数三：hierarchy（层次，等级），可选输出向量。包含图像的拓扑信息。每个轮廓对应4元组，分别对应后一个轮廓、前一个轮廓、父轮廓和内嵌轮廓。
参数四：flag 轮廓检索模式
参数五：flag 轮廓近似方法其中，对于参数二，它主要是以vector<cv::point>的形式保存寻找到的轮廓结果；
对于参数三，一般表示为cv::Vec4i 型的元素，并且进一步按照以下结构来进行定义：
Index | Meaning |
0 | 同级的下一条轮廓 |
1 | 同级的前一条轮廓 |
2 | 下级的第一个子节点 |
3 | 上级的父节点 |
通过这幅图能够很明显地看出层次关系：
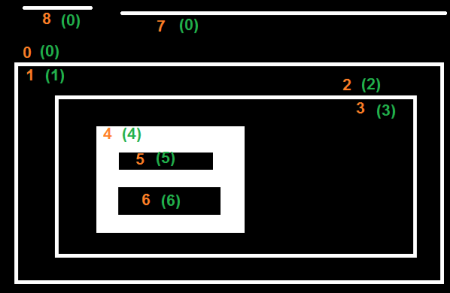
其对应的轮廓的相互关系为：
0 [ 7, -1, 1, -1]
1 [-1, -1, 2, 0]
2 [-1, -1, 3, 1]
3 [-1, -1, 4, 2]
4 [-1, -1, 5, 3]
5 [ 6, -1, -1, 4]
6 [-1, 5, -1, 4]
7 [ 8, 0, -1, -1]
8 [-1, 7, -1, -1]对于参数四，轮廓检索模式：
对于参数五，轮廓近似方法：
cv::CHAIN_APPROX_NONE
将轮廓编码中的所有点转换为点。 这一操作将会产生大量的点，每个点都将成为前一个点的8个邻点之一， 不会减少返回的点数，
cv::CHAIN_APPROX_SIMPLE
压缩水平、垂直、斜的部分，只保留最后一个点。 在许多特殊情况下，这一操作将大大减少返回的点数。 极端例子是，对于一个沿着x-y x-y 轴方向的矩形（任意大小）， 只会返回4个点。
cv::CHAIN_APPROX_TC89_L1 or cv::CHAIN_APPROX_TC89_KCOS
三、重要函数
轮廓处理中经常遇到的任务是计算一些轮廓变化的概括特性，这可能包括长度或其他一些反应轮廓整体大小的量度，包括以下函数：
cv::arcLength() 得到轮廓的长度
double cv::arcLength(
cv::InputArray points, // Array or vector of 2-dimensional points
bool closed // If true, assume link from last to first vertex
);第一个参数代表是轮廓，其形式可以是任何常见的轮廓表示方法（如标准模板库的点向量，或二通道数组）。
第二个参数closed表示该轮廓是否是闭合的。 假如轮廓是闭合的，则参数points中的最后一个点到第一个的距离也算入总弧长中。
cv::minAreaRect()活动轮廓的最小外接矩形
cv::RotatedRect cv::minAreaRect( // Return rectangle bounding the points
cv::InputArray points, // Array or vector of 2-dimensional points
);其返回的是一个RotatedRect 结构。
cv::minEnclosingCircle()获得最小包围圆
void cv::minEnclosingCircle(
cv::InputArray points, // Array or vector of 2-dimensional points
cv::Point2f& center, // Result location of circle center
float& radius // Result radius of circle
);center 和 radius 参数是需要获得的结果。
cv::convexHull()获得轮廓的凸包
void cv::convexHull(
cv::InputArray points, // Array or vector of 2-d points
cv::OutputArray hull, // Array of points or integer indices
bool clockwise = false, // true='output points will be clockwise'
bool returnPoints = true // true='points in hull', else indices
);pointPolygonTest 检测点是否落在多边形内
double cv::pointPolygonTest( // Return distance to boundary (or just side)
cv::InputArray contour, // Array or vector of 2-dimensional points
cv::Point2f pt, // Test point
bool measureDist // true 'return distance', else {0,+1,-1} only
);当参数measureDist设为真，函数将返回该点距离最近的轮廓边缘的距离。若点在轮廓内，距离为0；若点在轮廓外，距离将是大于0的整数
基于pointPolygonTest，我们能够实现“寻找已知轮廓最大内接圆”，具体来说，就是找到这样的结果：
四、快速连通区域分析
与轮廓分析紧密相关的另一种方法是连通区域分析. 采用阈值化等方法分割一张图像后，我们可以采用连通区域分析来有效地对返回图像逐张分离和处理。在以前，常用的方法是”是先调用 cv::findContours() 函数（传入cv::RETR_CCOMP 标志），随后在得到的连通区域上循环调用 cv::drawContours() “
比如，我在GOCVHelper中这样进行了实现
//寻找最大的轮廓
VP FindBigestContour(Mat src){
int imax = 0; //代表最大轮廓的序号
int imaxcontour = -1; //代表最大轮廓的大小
std::vector<std::vector<Point>>contours;
findContours(src,contours,CV_RETR_LIST,CV_CHAIN_APPROX_SIMPLE);
for (int i=0;i<contours.size();i++){
int itmp = contourArea(contours[i]);//这里采用的是轮廓大小
if (imaxcontour < itmp ){
imax = i;
imaxcontour = itmp;
}
}
return contours[imax];
}
//寻找并绘制出彩色联通区域
vector<VP> connection2(Mat src,Mat& draw){
draw = Mat::zeros(src.rows,src.cols,CV_8UC3);
vector<VP>contours;
findContours(src.clone(),contours,CV_RETR_LIST,CV_CHAIN_APPROX_SIMPLE);
//由于给大的区域着色会覆盖小的区域，所以首先进行排序操作
//冒泡排序，由小到大排序
VP vptmp;
for(int i=1;i<contours.size();i++){
for(int j=contours.size()-1;j>=i;j--){
if (contourArea(contours[j]) < contourArea(contours[j-1]))
{
vptmp = contours[j-1];
contours[j-1] = contours[j];
contours[j] = vptmp;
}
}
} }从OpenCV3开始实现专门函数 cv::connectedComponents() 和函数 cv::connectedComponentsWithStats()寻找
int cv::connectedComponents (
cv::InputArrayn image, // input 8-bit single-channel (binary)
cv::OutputArray labels, // output label map
int connectivity = 8, // 4- or 8-connected components
int ltype = CV_32S // Output label type (CV_32S or CV_16U)
);
int cv::connectedComponentsWithStats (
cv::InputArrayn image, // input 8-bit single-channel (binary)
cv::OutputArray labels, // output label map
cv::OutputArray stats, // Nx5 matrix (CV_32S) of statistics:[x0, y0, width0, height0, area0;... ; x(N-1), y(N-1), width(N-1),height(N-1), area(N-1)]
cv::OutputArray centroids, // Nx2 CV_64F matrix of centroids:[ cx0, cy0; ... ; cx(N-1), cy(N-1)]
int connectivity = 8, // 4- or 8-connected components
int ltype = CV_32S // Output label type (CV_32S or CV_16U)
);由于connectedComponentsWithStats是connectedComponents的增强版，所以我们主要介绍connectedComponentsWithStats。
参数二、labels用来保存寻找到的“联通区域”，以0-N用来表示当前像素属于该张图片的第几个轮廓；
这张动图是label的结果，可以看到有数值的区域表示的就是“第几个轮廓”
参数三、stats用来保存“联通区域”之间的关系，它是一个5XN的表格，可以直接使用ImageWtach打开。
分别对应各个轮廓的x,y,width,height和area。注意0的区域标识的是background，所以出现了(0,0)。
参数四、centroids对应的是轮廓的重点
五、矩
5.1什么是矩（moment） 数学定义：实函数相对于值c的n阶矩为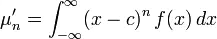 
从上述公式可以看到，它就是一个加了权重的积分，而权重是(x-c)n，其中n是阶数（n阶矩），如果把它想成一个平面直角系中，c是x轴上的一点，(x-c)n是个x点相对于c点值的n次方。以下是个积分的图示，只要想象一下，它的每个小方块再乘上权重：(xi-c)^n即可得到矩。
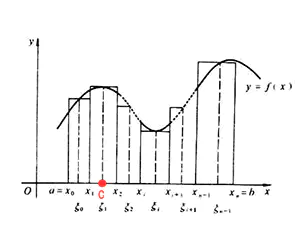轮廓处理中用到的矩，是它在统计学中的应用。以上公式是一元的情况，扩展到图片所在的二元，想象我们有一个图像矩阵，经过了寻找边缘，转换轮廓之后，矩阵中每个值点f(x,y)的值或为0（不是轮廓点），或为1（是轮廓点），当f(x,y)为0时，该积分项也为0，可以不计算，因此，对我们有意义的只有f(x,y)=1的n个点，即轮廓点。在后面公式中记为I(x,y)，x,y为其在图中的坐标，c点扩展到二元，可以视为轮廓的中心点，我们求得的所谓n阶中心矩，就如上述公式所示，积分的权重是轮廓上各点相对于中心位置c的n次方。此时我们可以得到一些统计规律，比如：轮廓边界长度（零阶矩），x/y方向上的均值（即质心，由一阶矩求得），方差（由二阶中心矩求得）,形状特性（Hu矩） 5.2. 常用的矩 1) 空间矩（spatial moment）i. 用途最简单地轮廓比较，只能用于对比位置，大小，角度完全一致的轮廓。一般来说轮廓矩代表了一条轮廓、一幅图像、一组点集的某些高级特征。
ii. 公式
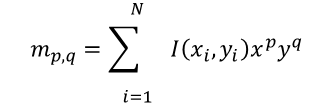
在上式中，mp,q代表对象中所有像素的总和，其中每个像素x, y的像素值都乘以因子 xpyq。. 在m00时，这个因子等于1。因此若图像为二值图（如，所有像素都等于0或者1），则 m00代表图像上所有值非零的区域。 当处理轮廓时，结果是轮廓的长度。
mpq表示图像的（p+q）阶矩，一般计算所有3阶的矩（p+q<=3）。其中 I(x,y) 是象素点 (x, y) 的值，一般是1，n是轮廓上点的个数，p和q分别是x维度和y维度上的矩，即m00,m10,m01…m03。
零阶矩m00是轮廓上点的简单累加，即轮廓上有多少个点 。
一阶矩m10，m01分别是x和y方向上的累加
2) 中心矩（central moment）
i. 用途
xavg和yavg由一阶矩和零阶矩的比值算出（见公式），它是重心坐标，中心矩即是根据x,y与重心的相对位置求取的矩，它使得结果与图像相对于x,y轴的位置无关（与平移无关）。
ii. 公式
将m10和m01分别除以 m00，能得到整个对象的平均x值和y值。
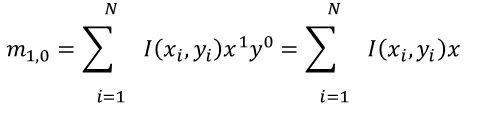
中心矩常用μp, q标注，定义如下
其中：
3) 归一化的中心矩
i. 用途
使用m00的幂对中心矩归一化，使得结果与图像大小无关
ii. 公式
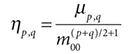
4) Hu不变矩
i. 用途
Hu矩是归一化中心矩的线性组合，它对于缩放，旋转，镜像映射具有不变性。
ii. 公式
最后，我想补充一下我认为适合轮廓分析的场合：
感谢阅读至此，希望有所帮助。