Stitching模块中focalsFromHomography初步研究

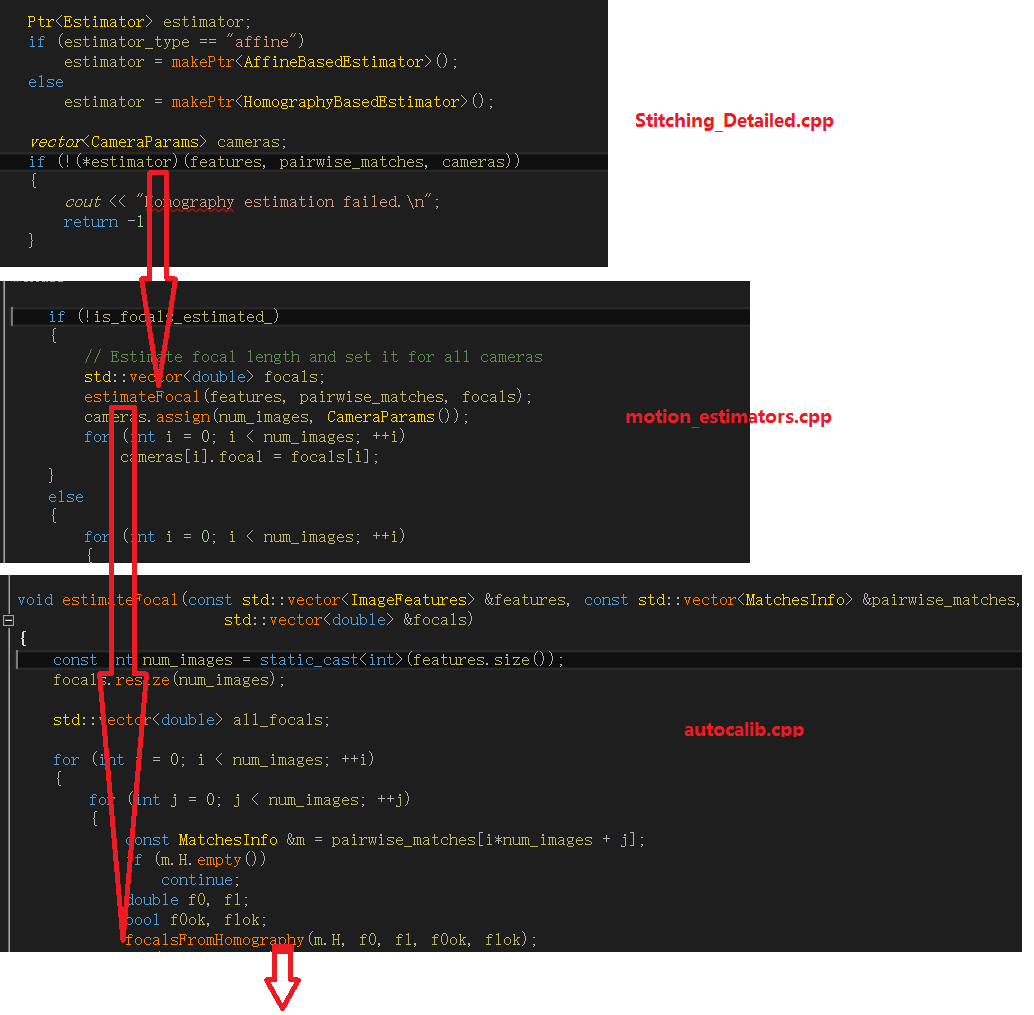
在Stitching模块中，通过“光束法平差”的时候，有一个步骤为“通过单应矩阵估算摄像头焦距”，调用的地方为：

 

void focalsFromHomography(const Mat& H, double &f0, double &f1, bool &f0_ok, bool &f1_ok)
{
    CV_Assert(H.type() == CV_64F && H.size() == Size(3, 3));
    const double* h = H.ptr<double>();
    double d1, d2; // Denominators
    double v1, v2; // Focal squares value candidates
    f1_ok = true;
    d1 = h[6] * h[7];
    d2 = (h[7] - h[6]) * (h[7] + h[6]);
    v1 = -(h[0] * h[1] + h[3] * h[4]) / d1;
    v2 = (h[0] * h[0] + h[3] * h[3] - h[1] * h[1] - h[4] * h[4]) / d2;
    if (v1 < v2) std::swap(v1, v2);
    if (v1 > 0 && v2 > 0) f1 = std::sqrt(std::abs(d1) > std::abs(d2) ? v1 : v2);
    else if (v1 > 0) f1 = std::sqrt(v1);
    else f1_ok = false;
    f0_ok = true;
    d1 = h[0] * h[3] + h[1] * h[4];
    d2 = h[0] * h[0] + h[1] * h[1] - h[3] * h[3] - h[4] * h[4];
    v1 = -h[2] * h[5] / d1;
    v2 = (h[5] * h[5] - h[2] * h[2]) / d2;
    if (v1 < v2) std::swap(v1, v2);
    if (v1 > 0 && v2 > 0) f0 = std::sqrt(std::abs(d1) > std::abs(d2) ? v1 : v2);
    else if (v1 > 0) f0 = std::sqrt(v1);
    else f0_ok = false;
}

本文具体分析focalsFromHomography，函数的参数定义：

     Tries to estimate focal lengths from the given homography  
     under the assumption that the camera undergoes rotations around its centre only.    
     Parameters  
     H – Homography.  
     f0 – Estimated focal length along X axis.  
     f1 – Estimated focal length along Y axis.  
     f0_ok – True, if f0 was estimated successfully, false otherwise.  
     f1_ok – True, if f1 was estimated successfully, false otherwise.  

 

可以看到它通过输入的单应矩阵，最后得到了相机焦距的估计值，计算的过程也比较复杂。那这样做的理由是什么了？具体计算的时候又是如何实现的了？

 

论文也就是算法的依据为《Construction of Panoramic Image Mosaics with Global and Local Alignment 》, Heung-Yeung Shum (hshum@microsoft.com) and Richard Szeliski (szeliski@microsoft.com)  page 17.method "focals from homgraphy matrix" 

我将具体的内容截出来：

 

原论文中40-44的推导，分为两个部分。一个部分是从“8参数”的变换，得出和x轴，y轴两个方向焦距的关系；一个部分是通过行列式的数学性质，计算出两个方向的焦距。这两个部分我目前都没有掌握足够的资料来进行证明，如果有能够证明的同学麻烦联系我一下。

然后来看算法实现。如果认为论文的表述是正确的，那么依据数学函数来对比c++的实现

代码中的h0-h8直接对应论文中的m0-m8,仅以f0来观察，那么f0^2可能有两种取值（这里x^2 是 x * x的一种简单表示方法，代表阶乘）

f0^2 = - m2*m5/(m0*m3+m1*m4)或f0^2 = m5^2 - m2^2 /(m0^2 + m1^2 - m3^2 - m4 ^2) 

看代码

 

d1 = h[0] * h[3] + h[1] * h[4];
那么
 v1 = -h[2] * h[5] / d1 =  -h[2] * h[5] /(h[0] * h[3] + h[1] * h[4])

 

 d2 = h[0] * h[0] + h[1] * h[1] - h[3] * h[3] - h[4] * h[4];
则
 v2 = (h[5] * h[5] - h[2] * h[2]) / d2 = (h[5] * h[5] - h[2] * h[2]) / （h[0] * h[0] + h[1] * h[1] - h[3] * h[3] - h[4] * h[4]）

 

前后是一一对应的，计算f0^2的两个值是没有问题的。但是这里f0有两个计算结果，最后选择哪个了？这一点在论文中没有说，在代码中采用的方法是首先判断v1,v2的符号，如果都是负数，那么肯定是计算错误了，因为它们所代表的f0^2肯定是非负数；然后判断v1,v2的大小，取其中比较大的那个来进行计算。

但是在

if (v1 > 0 && v2 > 0) f0 = std::sqrt(std::abs(d1) > std::abs(d2) ? v1 : v2);

我认为这样写是没有用的，我也在尝试联系一下相关对这个问题比较熟悉的人共同讨论。f1的计算方法是同样的。到这里已经得到f0和f1，分别对应x轴和y轴，为了得到最后的结果，那么会取

f = sqrt(f0 * f1) 

则得到这个当应矩阵的对于焦距的估计值。那么focalsFromHomography的一次运算也就结束了。