0.概述
我第一次听到网络流这个名词的时候觉得它会很高深,实际上学了之后还是很好理解的。
百度百科(看看就好,没几句人话)
最大流的概念直接看定义不好理解,我们来从一个实例引入:
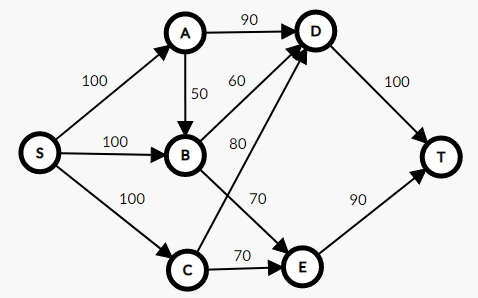
如图,(S)可以看成是一个水库(称作源点),有无限多的水,(T)可以看成是废水收集站(汇点),可以收集无限多的水。中间的点是一些村庄,村庄与源点、汇点以及村庄与村庄之间有一些单向的输水管道,每个管道都有一个固定的容量。问在不炸管道的情况下,汇点最多能收集到多少水(每个村庄进来的水量和出去的是一样的)。
我们很快就会有一个贪心的想法:先随便找路径,找到了就把流量减去这条路径上的最大流,直到找不到新的路径为止。
但这个想法是很容易被 hack 的:我们看这样一个图,
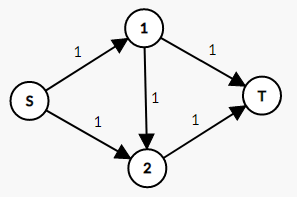
如果第一次随机扩展出(S
ightarrow1
ightarrow2
ightarrow T)这条路,增加了1的总流量,那么此时算法会认为我们没法继续走了,返回答案1。
很明显这个答案是错的,因为我们可以找到(S
ightarrow1
ightarrow T)和(S
ightarrow2
ightarrow T)两条路径使得答案为2。
计算机是不会看到整个图的,我们要给它一个选错边之后反悔的机会。说到反悔,很多人可能会想到搜索中的回溯,但是那样复杂度就不能保证了。这也是接下来我们讲到的网络流的精髓——反向边。
1. EK 算法
我们假设现在每条边都有一条初始流量为0的反向边,找出一条流量大于零的路径(又称增广路)时就把路径上所有边的容量减去该流量,反向边加上该流量。
我们继续按照刚才的方法找增广路,此时我们可以找到一条路径(S
ightarrow2
ightarrow1
ightarrow T)。中间经过了一条2到1的反向边,它表示什么意思呢?
如图,下面表示了走反向边的的意义:
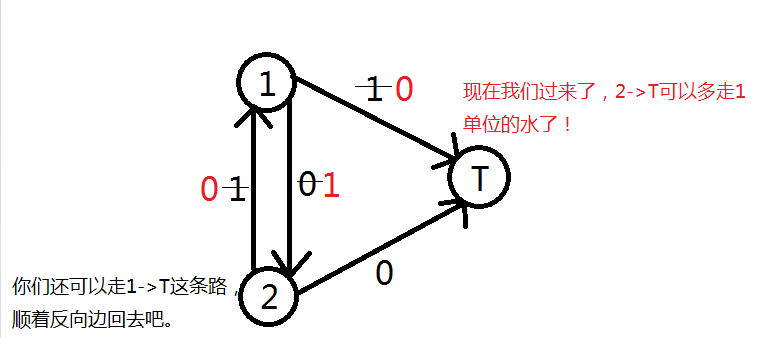
由此可见,反向边的作用就是打上一个标记,给程序反悔的机会并且避免了暴力回溯。
那么 EK 算法的框架也就出现了:每次 BFS 出一条增广路,然后修改每条边及其反向边的容量,将流量累加起来。
这只是核心思想,具体实现中有一些注意事项(例如反向边的实现等),会在代码中以注释提及。
洛谷P3376 【模板】网络最大流核心代码:
const int N=210,M=5010;
int n,m,s,t,ans;
int lst[N],vis[N];
struct Edge {
int to,nxt,flow;
}e[M<<1];
//此时cnt要等于一个奇数,我们让它等于-1,
//也就是说第一条边的编号为0,这样可以方便地利用异或求反向边
int hd[N],cnt=-1;
il void ade(int u,int v,int w){
e[++cnt].to=v,e[cnt].flow=w;
e[cnt].nxt=hd[u],hd[u]=cnt;
}
il bool BFS(){//返回有没有增广路(即能否走到汇点)
memset(vis,0,sizeof(vis));
memset(lst,0,sizeof(lst));
queue<int>q;
q.push(s),vis[s]=1;
while(!q.empty()){
int u=q.front();q.pop();
for(rg int i=hd[u];~i;i=e[i].nxt){
int v=e[i].to;
//根据增广路的定义,只走有流量的边
if(!vis[v]&&e[i].flow){
lst[v]=i;//记录当前增广路
if(v==t)return 1;
q.push(v),vis[v]=1;
}
}
}
return 0;
}
il void Update(){
int mxflow=INF,i;
for(rg int u=t;u!=s;u=e[i^1].to){//顺着反向边走到源点
i=lst[u],mxflow=min(mxflow,e[i].flow);
}
for(rg int u=t;u!=s;u=e[i^1].to){
i=lst[u];
//同时更新正向边和反向边
e[i].flow-=mxflow,e[i^1].flow+=mxflow;
}
ans+=mxflow;
}
il void EK(){
while(BFS()){
Update();//只要找到增广路就更新
}
}
signed main(){
memset(hd,-1,sizeof(hd));
Read(n),Read(m),Read(s),Read(t);
for(rg int i=1,u,v,w;i<=m;i++){
Read(u),Read(v),Read(w);
ade(u,v,w),ade(v,u,0);
}
EK();
cout<<ans<<endl;
return 0;
}
2. Dinic 算法
EK 算法一次只能找一条增广路,太慢了怎么办?于是就出现了 Dinic 算法。
与 EK 算法不同的是, Dinic 算法的 BFS 部分改为了将整个图分层,此时我们要求只能从一层走到下一层。
这样就可以实现求出最短增广路,避免绕远。
为了实现多路增广,我们写一个 DFS ,枚举一个点的所有出边,将流量加起来就得到了总流量。
下面给出同一个模板题的代码,注释相比 EK 的代码更加详尽,请结合注释来细致理解(由于代码是四个多月前写的所以码风有些许不同):
#define N 210
#define M 5010
int n,m,s,t,ans;
int vis[N],dep[N];//dep是每个点的层数
struct Edge {
//frm没有用,忽略即可(我也不知道当时是怎么想的)
int frm,to,nxt,wei;
}e[M<<1];
int head[N],cnt;
inline void ade(int u,int v,int w){
e[cnt].frm=u,e[cnt].to=v,e[cnt].wei=w;
e[cnt].nxt=head[u],head[u]=cnt++;
}
bool BFS(){//分层
memset(vis,0,sizeof(vis));
memset(dep,-1,sizeof(dep));
queue<int>q;
q.push(s),vis[s]=1,dep[s]=0;
while(!q.empty()){
int u=q.front();
q.pop();
for(rg int i=head[u];~i;i=e[i].nxt){
int v=e[i].to;
if(!vis[v]&&e[i].wei>0){//能走到的点才加入分层图
q.push(v),vis[v]=1,dep[v]=dep[u]+1;
}
}
}
return (dep[t]!=-1);//能否走到汇点(有没有增广路)
}
int DFS(int now,int flowin){//now节点流入了flowin,能流出多少
int flowout=0;
if(now==t)return flowin;//到了汇点直接返回
for(rg int i=head[now];~i&&flowin;i=e[i].nxt){
int v=e[i].to;
if(dep[v]==dep[now]+1&&e[i].wei>0){//只能走到下一层
int mxflow=DFS(v,min(flowin,e[i].wei));//继续往下流
if(!mxflow)dep[v]=-1;//这里是一个小优化:
//如果当前点流不下去了,那么它一定不能再对答案产生贡献
//此时将dep标为-1,表示不能再走这个点
e[i].wei-=mxflow,e[i^1].wei+=mxflow;//与EK同样的做法
flowin-=mxflow,flowout+=mxflow;
}
}
return flowout;
}
void Dinic(){
while(BFS()){//只要有增广路就不断流
ans+=DFS(s,INF);
}
}
signed main(){
Read(n),Read(m),Read(s),Read(t);
memset(head,-1,sizeof(head));
for(rg int i=1;i<=m;i++){
int u,v,w;
Read(u),Read(v),Read(w);
ade(u,v,w),ade(v,u,0);
}
Dinic();
cout<<ans<<endl;
return 0;
}
另外要注意的是,无论是 EK 还是 Dinic ,都有一些小细节:
由于边从0开始编号,head数组要赋为-1,遍历时不能写for(int i=hd[u];i;i=e[i].nxt)而是~i或i!=-1。(我被坑过无数次了)
BFS 前记得把vis什么的初始化一遍。
注意数据范围,例如洛谷的模板题就需要开long long。
3.应用
你可能会问,刚刚讲了这么一大堆乱七八糟的,网络流到底有什么用呢?我们来看几个例题:
例题一:洛谷P2756 飞行员配对方案问题
相信来学网络流的各位都接触过二分图匹配,现在告诉你,它也可以用网络流做!
我们知道网络流需要有源点和汇点,那我们就人为给它创造出一个。
更具体地,从超级源点 S 向所有点连一条容量为1的边,再从所有点向超级汇点 T 连一条容量为1的边,点之间再按照题目要求连容量为1的边。
那么这时候如果手玩一下就会发现,这个图的最大流就是二分图的最大匹配!
感性理解一下:一个点只能流进来1,表示只能匹配1个,那么我们要找到最多条匹配边,实际上就是求一个最大流。
此题要记录方案怎么办? DFS 时顺便记录一下就好了。
用 Dinic 做二分图匹配的复杂度据说是(O(nsqrt{m}))的但我显然不会证。
代码留作练习。(其实是作者懒得写了qvq)
例题二:洛谷P2891 [USACO07OPEN]Dining G
相信根据刚刚的经验大家可以yy出一种简单的建图方式:超级源点连食物,食物连奶牛,奶牛连饮料,饮料连超级汇点。
但是如果仔细读题的话会发现这个连法很明显是错误的:每头奶牛只能选一种食物和饮料,这样连边会导致一头牛连多个食物和饮料。
为了满足这个限制我们需要让一头牛只流过1单位的水,那么我们可以把一头牛拆成两个点,中间连一条容量为1的边,就保证了一头牛只对应一种食物和饮料。
最终顺序是:超级源点->食物->奶牛1->奶牛2->饮料->超级汇点(每条边容量都是1)。
#define N 4100
#define M 203100
int n,f,d,s,t,ans;
int vis[N],dep[N];
struct Edge {
int to,nxt,wei;
}e[M<<1];
int head[N],cnt;
inline void ade(int u,int v,int w){
e[cnt].to=v,e[cnt].wei=w;
e[cnt].nxt=head[u],head[u]=cnt++;
}
bool BFS(){
memset(vis,0,sizeof(vis));
memset(dep,-1,sizeof(dep));
queue<int>q;
q.push(s),vis[s]=1,dep[s]=0;
while(!q.empty()){
int u=q.front();
q.pop();
for(rg int i=head[u];~i;i=e[i].nxt){
int v=e[i].to;
if(!vis[v]&&e[i].wei>0){
q.push(v),vis[v]=1,dep[v]=dep[u]+1;
}
}
}
return (dep[t]!=-1);
}
int DFS(int now,int flowin){
int flowout=0;
if(now==t)return flowin;
for(rg int i=head[now];~i&&flowin;i=e[i].nxt){
int v=e[i].to;
if(dep[v]==dep[now]+1&&e[i].wei>0){
int mxflow=DFS(v,min(flowin,e[i].wei));
if(!mxflow)dep[v]=-1;
e[i].wei-=mxflow,e[i^1].wei+=mxflow;
flowin-=mxflow,flowout+=mxflow;
}
}
return flowout;
}
void Dinic(){
while(BFS()){
ans+=DFS(s,INF);
}
}
int main(){
Read(n),Read(f),Read(d);
s=0,t=2*n+f+d+1;
memset(head,-1,sizeof(head));
for(rg int i=1;i<=f;i++)ade(s,i,1),ade(i,s,0);//超级源点连食物
for(rg int i=1;i<=d;i++)ade(f+2*n+i,t,1),ade(t,f+2*n+i,0);//饮料连超级汇点
for(rg int i=1;i<=n;i++)ade(f+i,f+n+i,1),ade(f+n+i,f+i,0);//奶牛拆点连自己
for(rg int i=1;i<=n;i++){
int fi,di,ff,dd;
Read(fi),Read(di);
for(rg int j=1;j<=fi;j++){//食物连奶牛1
Read(ff);
ade(ff,f+i,1),ade(f+i,ff,0);
}
for(rg int j=1;j<=di;j++){//奶牛2连饮料
Read(dd);
ade(f+n+i,f+2*n+dd,1),ade(f+2*n+dd,f+n+i,0);
}
}
Dinic();
cout<<ans<<endl;
return 0;
}
例题三:洛谷P2598 [ZJOI2009]狼和羊的故事
超级源点连到所有狼的领地,所有羊的领地连到超级汇点(两组边容量均为INF),每个点向四周的点连容量为1的边(表示可以走到)。
那么如何才算是将狼和羊分开了呢?我们发现,只要源点不能到达汇点,也就意味着所有狼点都不能通过一些路径走到羊点,此时狼和羊就分开了。而题目的要求篱笆最短也就是让我们求最小割。
最小割和最大流有什么关系呢?事实上,它们是相等的!具体证明可以上网找最小割最大流定理。
那么我们就成功切掉了这个题:
#define N 100010
int n,m,s,t,ans,mp[110][110];
int dep[N],vis[N];
struct Edge {
int to,nxt,wei;
}e[N<<1];
int head[N],cnt;
inline void ade(int u,int v,int w){
e[cnt].to=v,e[cnt].wei=w;
e[cnt].nxt=head[u],head[u]=cnt++;
e[cnt].to=u,e[cnt].wei=0;
e[cnt].nxt=head[v],head[v]=cnt++;
}
bool BFS(){
memset(dep,-1,sizeof(dep));
memset(vis,0,sizeof(vis));
queue<int>q;
q.push(s),dep[s]=0,vis[s]=1;
while(!q.empty()){
int u=q.front();
q.pop();
for(rg int i=head[u];~i;i=e[i].nxt){
int v=e[i].to;
if(!vis[v]&&e[i].wei>0){
q.push(v),dep[v]=dep[u]+1,vis[v]=1;
}
}
}
return (dep[t]!=-1);
}
int DFS(int now,int flowin){
int flowout=0;
if(now==t)return flowin;
for(rg int i=head[now];~i;i=e[i].nxt){
int v=e[i].to;
if(dep[v]==dep[now]+1&&e[i].wei>0){
int mxflow=DFS(v,min(flowin,e[i].wei));
if(!mxflow)dep[v]=-1;
e[i].wei-=mxflow,e[i^1].wei+=mxflow;
flowin-=mxflow,flowout+=mxflow;
}
}
return flowout;
}
void Dinic(){
while(BFS()){
ans+=DFS(s,INF);
}
}
int dx[4]={1,0,-1,0};
int dy[4]={0,1,0,-1};
inline int Idx(int x,int y){
return (x-1)*m+y;
}
int main(){
Read(n),Read(m);
memset(head,-1,sizeof(head));
s=0,t=n*m+1;
for(rg int i=1;i<=n;i++){
for(rg int j=1;j<=m;j++){
Read(mp[i][j]);
if(mp[i][j]==1)ade(s,Idx(i,j),INF);
else if(mp[i][j]==2)ade(Idx(i,j),t,INF);
}
}
for(rg int i=1;i<=n;i++){
for(rg int j=1;j<=m;j++){
for(rg int k=0;k<4;k++){
int xx=i+dx[k],yy=j+dy[k];
if(xx&&yy&&xx<=n&&yy<=m){
if(mp[xx][yy]!=1&&mp[i][j]!=2){
ade(Idx(i,j),Idx(xx,yy),1);
}
}
}
}
}
Dinic();
cout<<ans<<endl;
return 0;
}
由上面几个例题可以看出,大多数时候网络流的关键在于建图,如何将一个不像网络流的题转化为网络流,是大家做题时需要考虑的。
4.总结
网络流有许多分支及应用,这篇博客只讲解了最大流的 EK 和 Dinic 算法,还有它们的一些优化以及玄学的 ISAP 和 HLPP 算法没有提及(但是作者也不会)。
另外如果把边加上一个单位流量的花费,就变成了费用流,这是我们下期博客要讨论的话题。
总而言之,网络流是一种省选及以上范围内用途广泛的一种模型,一定要掌握透彻。