•给定一个中序遍历为1,2,3,…,n的二叉树
•每个结点有一个权值
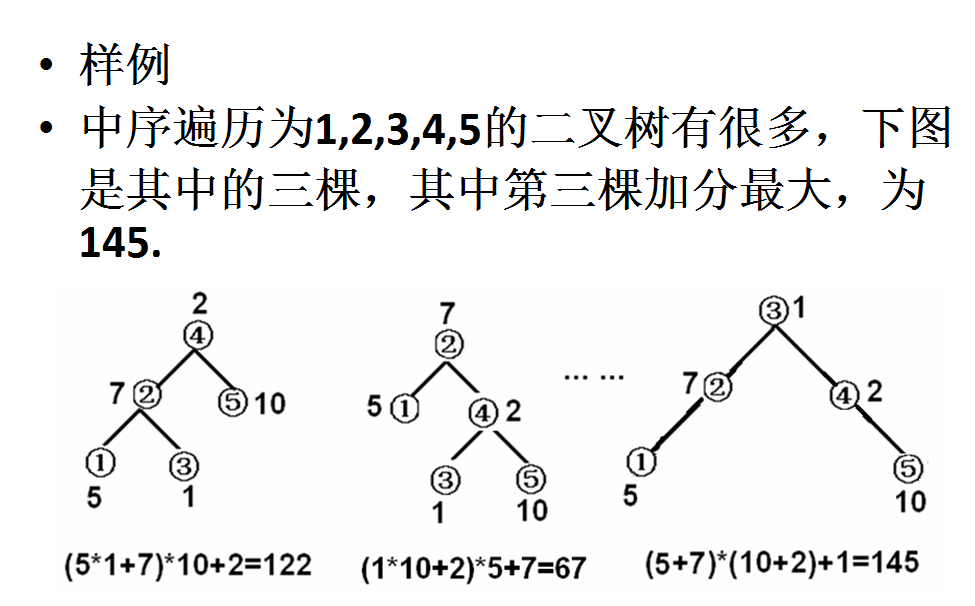
•定义二叉树的加分规则为:
–左子树的加分×右子树的加分+根的分数
–若某个树缺少左子树或右子树,规定缺少的子树加分为1。
•构造符合条件的二叉树
–该树加分最大
–输出其前序遍历序列
定义dp[i][j] 为中序遍历为i-->j的二叉树的最大加分
那么dp[i][j] = max{dp[i][k-1] * dp[k+1][j] + a[k]; i<=k<=j}
其实就相当于区间dp,只不过是在树上而已
输入样例:
5
5 7 1 2 10
5 7 1 2 10
1 #include <stdio.h> 2 #include <string.h> 3 4 int a[30]; 5 int dp[30][30];//dp[i][j] 表示某子树的中序遍历为i-->j 那么dp[i][i]则表示i为叶子结点 6 int root[30][30]; 7 8 void print(int i, int j) 9 { 10 if(i>j)return; 11 if(root[i][j]==-1) return; 12 printf("%d ",root[i][j]+1); 13 print(i,root[i][j]-1); 14 print(root[i][j]+1,j); 15 } 16 int main() 17 { 18 int n,i,j,k,t; 19 while(scanf("%d",&n)!=EOF) 20 { 21 memset(dp,-1,sizeof(dp)); 22 memset(root,-1,sizeof(root)); 23 for(i=0; i<n; ++i) 24 { 25 scanf("%d",&a[i]); 26 dp[i][i] = a[i]; 27 root[i][i] = i; 28 } 29 for(t=1; t<n; ++t)//枚举长度 30 for(i=0; i<n-t; ++i)//枚举起点 31 { 32 j = t + i;//区间总长度 33 for(k=i+1; k<j; ++k) 34 if(dp[i][j] < (dp[i][k-1]*dp[k+1][j]+a[k])) 35 { 36 dp[i][j] = dp[i][k-1]*dp[k+1][j]+a[k]; 37 root[i][j] = k; 38 } 39 if(dp[i][j] < dp[i][j-1] + a[j]) 40 { 41 dp[i][j] = dp[i][j-1] + a[j]; 42 root[i][j] = j; 43 } 44 if(dp[i][j] < dp[i+1][j] + a[i]) 45 { 46 dp[i][j] = dp[i+1][j] + a[i]; 47 root[i][j] = i; 48 } 49 } 50 printf("%d ",dp[0][n-1]); 51 print(0,n-1); 52 } 53 }