摘要:最近在学习机器学习/数据挖掘的算法,在看一些paper的时候经常会遇到以前学过的数学公式或者名词,又是总是想不起来,所以在此记录下自己的数学复习过程,方便后面查阅。
1:数学期望
数学期望是随机变量的重要特征之一,随机变量X的数学期望记为E(X),E(X)是X的算术平均的近似值,数学期望表示了X的平均值大小。
- 当X为离散型随机变量时,并且其分布律为 P(X=xk) = pk ,其中k=1,2,…,n;则数学期望
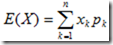 (要求绝对收敛).
(要求绝对收敛). - 当X为连续型随机变量时,设其概率密度为f(x),则数学期望为
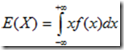 (要求绝对收敛).
(要求绝对收敛).
2: 方差
数学期望给出了随机变量的平均大小,现实生活中我们还经常关心随机变量的取值在均值周围的散布程度,而方差就是这样的一个数字特征。
设X是随机变量,并且E{[X-E(X)2]}存在,则称它为X的方差,记为D(X)。
另外,D(X) = E{[X-E(X)2]} 经过化解可得 D(X) = E(X2) – [E(X)]2 .我们一般计算的时候常用这个式子。
3: 协方差
对于二维的随机变量(X,Y),我们还要讨论它们的相互关系,协方差就是一个这样的数字特征。
因为E{[X-E(X)][Y-E[Y]]} = E(XY) – E(X)E(Y).
又当X,Y相互独立的时候E(XY) = E(X)E(Y).这意味着若E{[X-E(X)][Y-E[Y]]} ≠ 0 ,则X与Y是存在一定关系的。
我们把E{[X-E(X)][Y-E[Y]]} 称为随机变量X与Y的协方差。记为Cov(X,Y).
即:Cov(X,Y) = E{[X-E(X)][Y-E[Y]]}
4:相关系数
协方差在某种意义上是表示了两个随机变量间的关系,但是Cov(X,Y)的取值大小与X,Y的量纲有关,不方便分析,所以为了避免这一点,我们用X,Y的标准化随机变量来讨论。
其中![]() 为X,Y的协方差即Cov(X,Y),D(X),D(Y)分别是X,Y的方差且D(X)>0,D(Y)>0。
为X,Y的协方差即Cov(X,Y),D(X),D(Y)分别是X,Y的方差且D(X)>0,D(Y)>0。
关于相关系数,我们有下面的性质:
- |
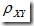 | ≤ 1
| ≤ 1 - |
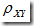 | = 1 的充要条件是X 与 Y 以概率 1 存在线性关系,即 P{Y = a +bX} = 1, a,b是常数。
| = 1 的充要条件是X 与 Y 以概率 1 存在线性关系,即 P{Y = a +bX} = 1, a,b是常数。 - 若
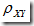 = 0,则说明X,Y不相关并且X与Y不存在线性关系。
= 0,则说明X,Y不相关并且X与Y不存在线性关系。 - 若随机变量X,Y相互独立,则
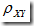 = 0,即X,Y不相关。
= 0,即X,Y不相关。
注意:两个不相关的随机变量,不一定相互独立,有一特殊情况是,当随机变量X,Y服从二维正态分布的时候,独立与不相关等价。
- 不相关只能说明X与Y不存在线性关系。
- 独立说明X与Y既不存在线性关系,也不存在非线性关系。
5:矩
矩(moment)是最广泛的一种数字特征,常用的矩有两种:原点矩和中心矩。
原点矩:
对于正整数k,称随机变量X的k次幂的数学期望为X的k阶原点矩:即 E(Xk) ,k=1,2,…n.
数学期望就是一阶原点矩。
中心矩:
对于正整数k,称随机变量X与E(X)差的k次幂的数学期望为X的k阶中心矩:即 E{X-E[XK]},K=1,2,…n.
方差就是二阶中心矩。