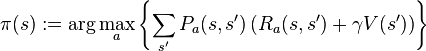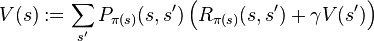Markov Decision Processes (MDPs)
Named after Andrey Markov, known at least as early as 1950s.(cf. Bellman 1957)
Discrete time stochastic control process.
State:
Action:
Reward:
Markov property: given s and a , it conditionally independen of all previous state and actions.
Extent of Markov chains:
Diff.: addition of actions (allowing choice) and rewards (giving motivation).
Formally,
Defination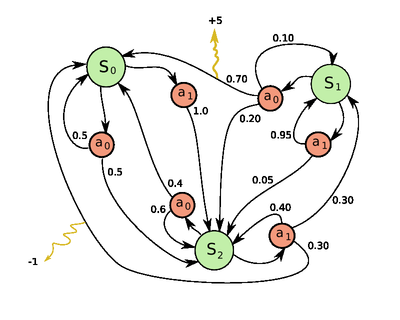
a 4-tuple (S,A,P.(.,.),R.(.,.), where
- S is a finite set of states,
- A is a finite set of actions (alternatively, A_s is the finite set of actions available from state s),
- P_a(s, s’) = Pr(s_{t+1} = s’ | s_t = s, a_t = a) is the probability that action a in state s at time t will lead to state s’ at time t+1
- R_a(s,s’) is the immediate reward (or expected immediate reward) received after transition to state s’ from state s with transition probability P_a(s,s’)
Problem
Find a policy for decision maker: a function \pai that specifies that action \pai 9s) that the decision maker will choose when in state s.
The goal is to choose a policy \pai that will maximize some cumulative function of random rewards:
\sum_{t=0]{\gama^t R_{a_t}(s_t,s_{t+1}) (where a_t = \pai (s_t})
where \gama is the discount rate and \in (0,1]. It is typically close to 1.
Algorithm
P : transition function
R: Reward function
V: contains real values, V(s) will contain the discounted sum of the rewards to be earned (on average ) bye following that solution from state s.
Notable variants
Value iteration
Polycy iteration \ Modified policy iteration\ Prioritized sweeping
Extension and generalizations
Partial observability (POMDP)
RL:
Probilities or rewards are unknown.
Q(s,a) = \sum_{s’}{Pa(s,s])(R_a{s,s]) + \gammaV(s’))}
I was in state s and I tried doing a and s’ happened.