字符串相关问题 及 后缀树

这一节主要简单讨论几个跟字符串相关的问题，主题可能会在后面陆续增加。

子串问题用的最多的方法就是动态规划算法和后缀树（见文尾）、Trie。当然其他如hash table，堆等等也需要考虑。有时也可能要配合MAP使用。

1 字符串精确匹配

1.1 KMP算法

　　KMP主要是利用模式串的最大相同后缀前缀长度。有了模式串在各个位置的这个长度，当与目标串在某个位置不匹配时，可以跳过模式串的这个长度的距离，避免重复的字符串比较。模式串的最大相同后缀前缀长度序列的构建，其实跟后面字符串匹配类似，只是把目标串换成了自己。

详情参照“从头到尾彻底理解KMP”：http://www.cnblogs.com/zhangtianq/p/5839909.html

1.2 连续子串

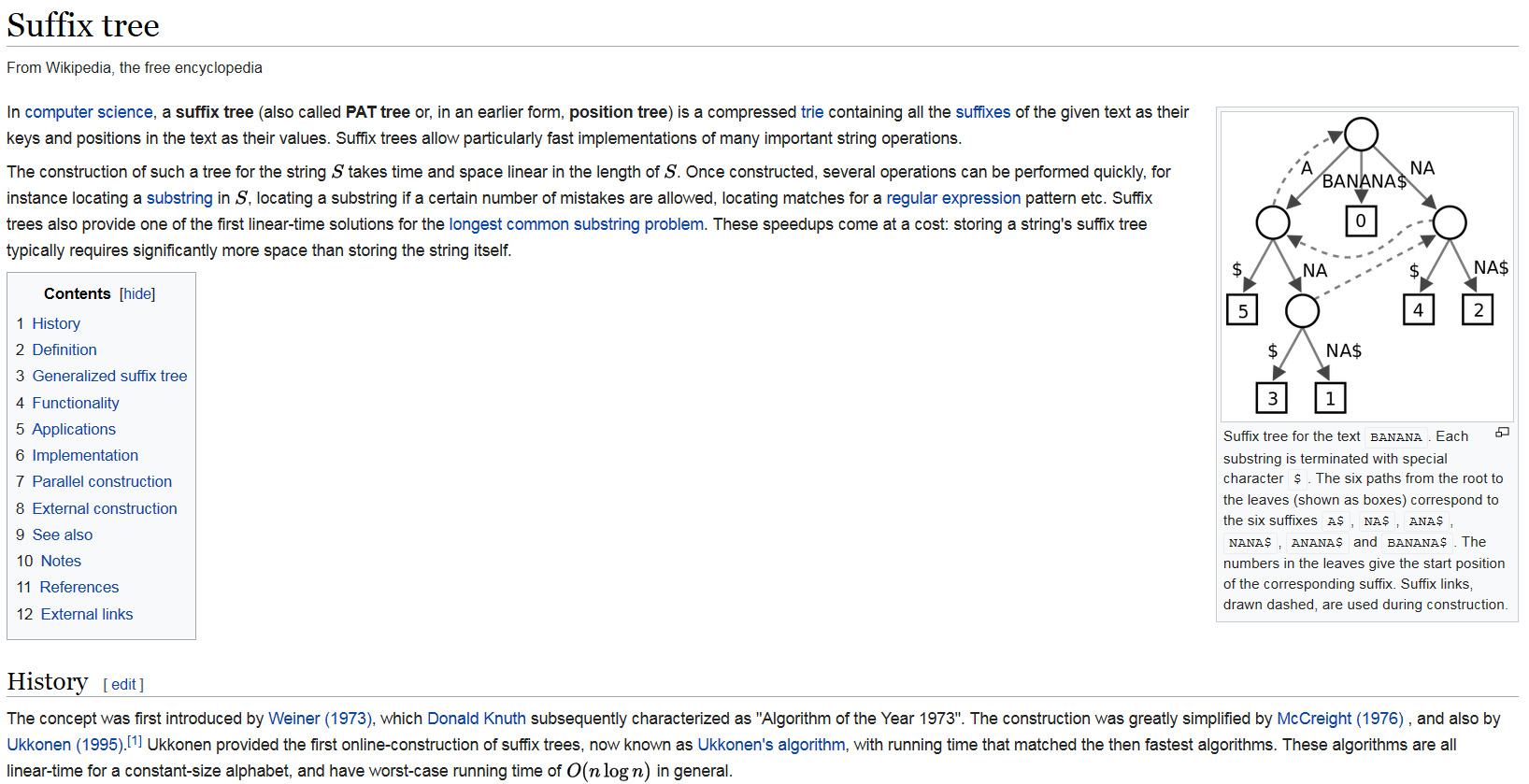
单个或多个字符串的最长连续重复子串：后缀树

重复次数达到k次的子串：后缀树

最长回文子串：动态规划，Manacher法

2 字符串模糊匹配

2.1 k-近似匹配（允许k个不匹配）：

　　　字符串S和P的编辑距离k：动态规划，dist[i][j] = min(dist[i-1][j] + 1, dist[i][j-1] + 1, dist[i-1][j-1] + (S[i]==P[j])?0:1)

　　　做一下改进用于k-近似匹配，参考 “动态规划 近似串匹配”。主要区别是第一行的初始值不一样。算完整串的编辑距离，S[i]与P的空子串的编辑距离是i，而k-近似匹配时，因为S的子串可以从任意位置开　       始，所以初始编辑距离为0。

　　　或者通过后缀树，查找节点的最近公共父节点（待考）

2.2 固定空隙长度子串（k个%， maximal gapped motifs)

 　　后缀树相关（待补充）

2.3 随机空隙长度子串（*）

　　动态规划：字符串S和模式p，当p[j]==‘*’，dp[i][j]=1 if dp[i][j-1] or dp[i-1][j-1]。若此时dp[i][j]==1，则dp[i~n][j]=1

2.4 最长公共子序列LCS

 类似上面编辑距离， A和B的LCS[i][j] = (A[i]==B[j])? 1+LCS[i-1][j-1] : max(LCS[i-1][j], LCS[i][j-1]),

3 词频统计

 Trie（前缀树/字典树）及其应用 应用场景3

其他参考

后缀树及模式匹配 https://wenku.baidu.com/view/75ae114cc850ad02de804110.html

“in the search of motifs (and other hidden structures)”：http://www.doc88.com/p-9923369128588.html

维基百科“Suffix tree”：https://en.wikipedia.org/wiki/Suffix_tree

http://blog.sina.com.cn/s/blog_a02991400101gl3o.html

Suffix tree

Notes

• Giegerich & Kurtz (1997).
• http://www.cs.uoi.gr/~kblekas/courses/bioinformatics/Suffix_Trees1.pdf
• Farach (1997).
• Gusfield (1999), p.92.
• Gusfield (1999), p.123.
• Baeza-Yates & Gonnet (1996).
• Gusfield (1999), p.132.
• Gusfield (1999), p.125.
• Gusfield (1999), p.144.
• Gusfield (1999), p.166.
• Gusfield (1999), Chapter 8.
• Gusfield (1999), p.196.
• Gusfield (1999), p.200.
• Gusfield (1999), p.198.
• Gusfield (1999), p.201.
• Gusfield (1999), p.204.
• Gusfield (1999), p.205.
• Gusfield (1999), pp.197–199.
• Allison, L. "Suffix Trees". Retrieved 2008-10-14.
• First introduced by Zamir & Etzioni (1998).
• Apostolico et al.
• Hariharan (1994).
• Sahinalp & Vishkin (1994).
• Farach & Muthukrishnan (1996).
• Iliopoulos & Rytter (2004).
• Shun & Blelloch (2014).
• Smyth (2003).
• Tata, Hankins & Patel (2003).
• Phoophakdee & Zaki (2007).
• Barsky et al. (2008).
• Barsky et al. (2009).

32. Mansour et al. (2011).

References

• Apostolico, A.; Iliopoulos, C.; Landau, G. M.; Schieber, B.; Vishkin, U. (1988), "Parallel construction of a suffix tree with applications", Algorithmica, 3.
• Baeza-Yates, Ricardo A.; Gonnet, Gaston H. (1996), "Fast text searching for regular expressions or automaton searching on tries", Journal of the ACM, 43 (6): 915–936, doi:10.1145/235809.235810.
• Barsky, Marina; Stege, Ulrike; Thomo, Alex; Upton, Chris (2008), "A new method for indexing genomes using on-disk suffix trees", CIKM '08: Proceedings of the 17th ACM Conference on Information and Knowledge Management, New York, NY, USA: ACM, pp. 649–658.
• Barsky, Marina; Stege, Ulrike; Thomo, Alex; Upton, Chris (2009), "Suffix trees for very large genomic sequences", CIKM '09: Proceedings of the 18th ACM Conference on Information and Knowledge Management, New York, NY, USA: ACM.
• Farach, Martin (1997), "Optimal Suffix Tree Construction with Large Alphabets" (PDF), 38th IEEE Symposium on Foundations of Computer Science (FOCS '97), pp. 137–143.
• Farach, Martin; Muthukrishnan, S. (1996), "Optimal Logarithmic Time Randomized Suffix Tree Construction", International Colloquium on Automata Languages and Programming.
• Farach-Colton, Martin; Ferragina, Paolo; Muthukrishnan, S. (2000), "On the sorting-complexity of suffix tree construction.", Journal of the ACM, 47 (6): 987–1011, doi:10.1145/355541.355547.
• Giegerich, R.; Kurtz, S. (1997), "From Ukkonen to McCreight and Weiner: A Unifying View of Linear-Time Suffix Tree Construction" (PDF), Algorithmica, 19 (3): 331–353, doi:10.1007/PL00009177.
• Gusfield, Dan (1999), Algorithms on Strings, Trees and Sequences: Computer Science and Computational Biology, Cambridge University Press, ISBN 0-521-58519-8.
• Hariharan, Ramesh (1994), "Optimal Parallel Suffix Tree Construction", ACM Symposium on Theory of Computing.
• Iliopoulos, Costas; Rytter, Wojciech (2004), "On Parallel Transformations of Suffix Arrays into Suffix Trees", 15th Australasian Workshop on Combinatorial Algorithms.
• Mansour, Essam; Allam, Amin; Skiadopoulos, Spiros; Kalnis, Panos (2011), "ERA: Efficient Serial and Parallel Suffix Tree Construction for Very Long Strings" (PDF), PVLDB, 5 (1): 49–60, doi:10.14778/2047485.2047490.
• McCreight, Edward M. (1976), "A Space-Economical Suffix Tree Construction Algorithm", Journal of the ACM, 23 (2): 262–272, CiteSeerX 10.1.1.130.8022 , doi:10.1145/321941.321946.
• Phoophakdee, Benjarath; Zaki, Mohammed J. (2007), "Genome-scale disk-based suffix tree indexing", SIGMOD '07: Proceedings of the ACM SIGMOD International Conference on Management of Data, New York, NY, USA: ACM, pp. 833–844.
• Sahinalp, Cenk; Vishkin, Uzi (1994), "Symmetry breaking for suffix tree construction", ACM Symposium on Theory of Computing
• Smyth, William (2003), Computing Patterns in Strings, Addison-Wesley.
• Shun, Julian; Blelloch, Guy E. (2014), "A Simple Parallel Cartesian Tree Algorithm and its Application to Parallel Suffix Tree Construction", ACM Transactions on Parallel Computing.
• Tata, Sandeep; Hankins, Richard A.; Patel, Jignesh M. (2003), "Practical Suffix Tree Construction", VLDB '03: Proceedings of the 30th International Conference on Very Large Data Bases, Morgan Kaufmann, pp. 36–47.
• Ukkonen, E. (1995), "On-line construction of suffix trees" (PDF), Algorithmica, 14 (3): 249–260, doi:10.1007/BF01206331.
• Weiner, P. (1973), "Linear pattern matching algorithms" (PDF), 14th Annual IEEE Symposium on Switching and Automata Theory, pp. 1–11, doi:10.1109/SWAT.1973.13.
• Zamir, Oren; Etzioni, Oren (1998), "Web document clustering: a feasibility demonstration", SIGIR '98: Proceedings of the 21st annual international ACM SIGIR conference on Research and development in information retrieval, New York, NY, USA: ACM, pp. 46–54.

External links

• Suffix Trees by Sartaj Sahni
• NIST's Dictionary of Algorithms and Data Structures: Suffix Tree
• Universal Data Compression Based on the Burrows-Wheeler Transformation: Theory and Practice, application of suffix trees in the BWT
• Theory and Practice of Succinct Data Structures, C++ implementation of a compressed suffix tree
• Ukkonen's Suffix Tree Implementation in C Part 1 Part 2 Part 3 Part 4 Part 5 Part 6