SVM发展史

线性SVM=线性分类器+最大间隔
间隔(margin):边界的活动范围。The margin of a linear classifier is defined as the width that the boundary could be increased by before hitting a data point.
预备知识
- 线性分类器的分割平面(超平面):
Wx+b=0 - 点到超平面的距离:(M=frac{ vert g(x) vert }{left|W ight| }),其中(g(x)=Wx+b)
- SVM中正样本定义为g(x)>=1,负样本定义为g(x)<=-1
- SVM中Wx+b=1或者Wx+b=-1的点称为支持向量
间隔的形式化描述
(M=frac{2}{left|W
ight| })
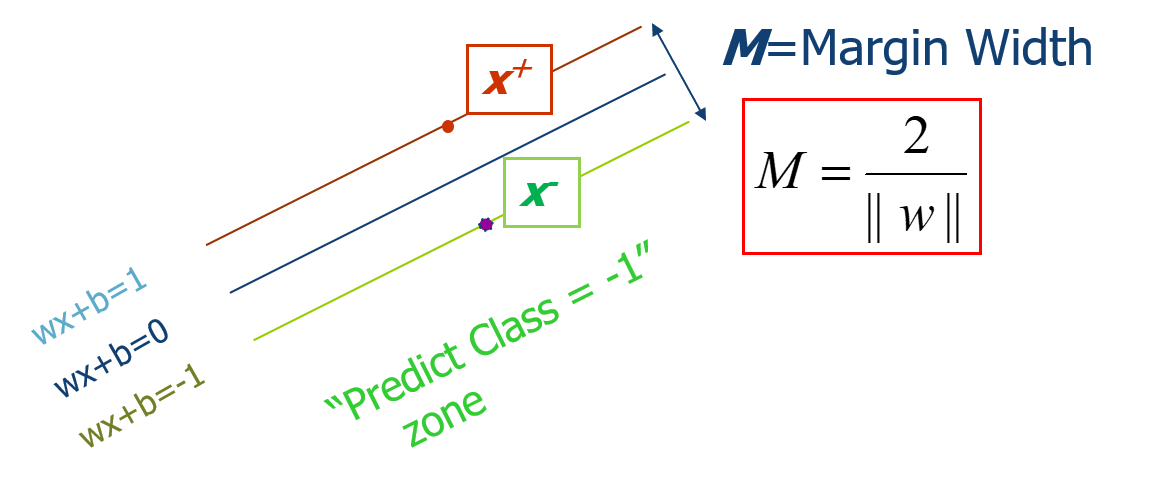
SVM通过最大化M来求解参数W和b的,目标函数如下:
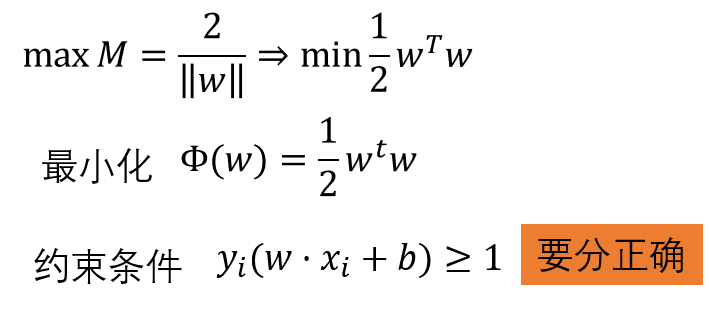
求解 :拉格朗日乘数法,偏导为0后回带
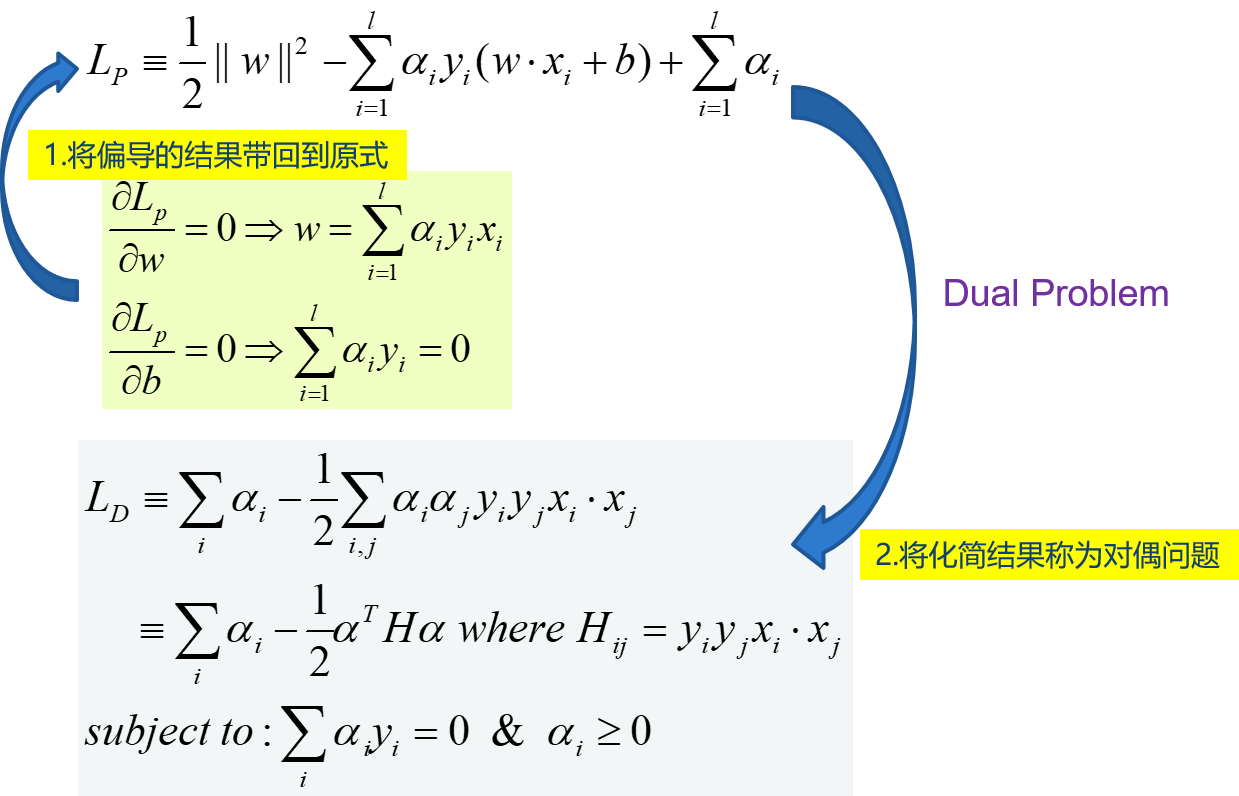
在SVM中,原问题和对偶问题具有相同的解,W已经求出:(W=sum_{i=1}^{l}{alpha_iy_ix_i}), 不等式约束,还需要满足KKT条件。若(alpha_i>0),则必有xi为支持向量,即:训练完毕后,最终模型仅和支持向量有关。

b的求解过程如下

一个实例

软间隔:加入容错量
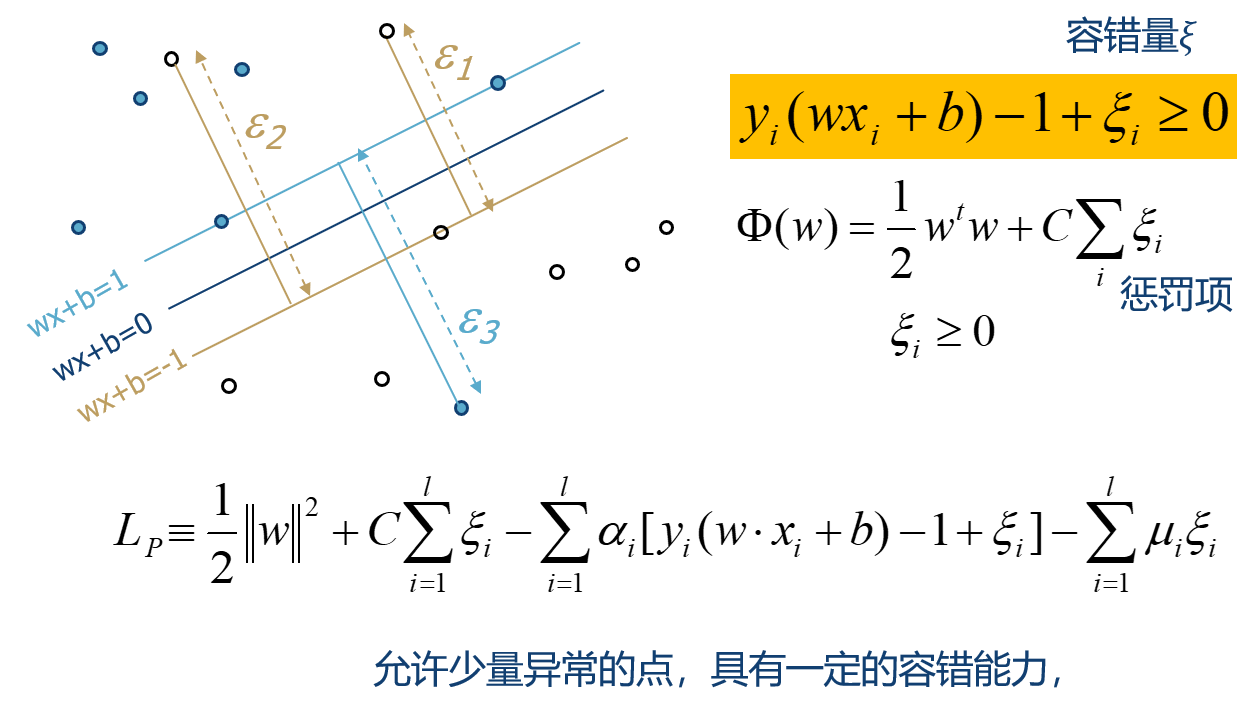
同样采用拉格朗日乘数法求解
LD的区别仅仅体现为(alpha_i)的约束不同。

非线性SVM:特征空间
通过映射到高维空间来将线性不可分的问题转换为线性可分的问题。
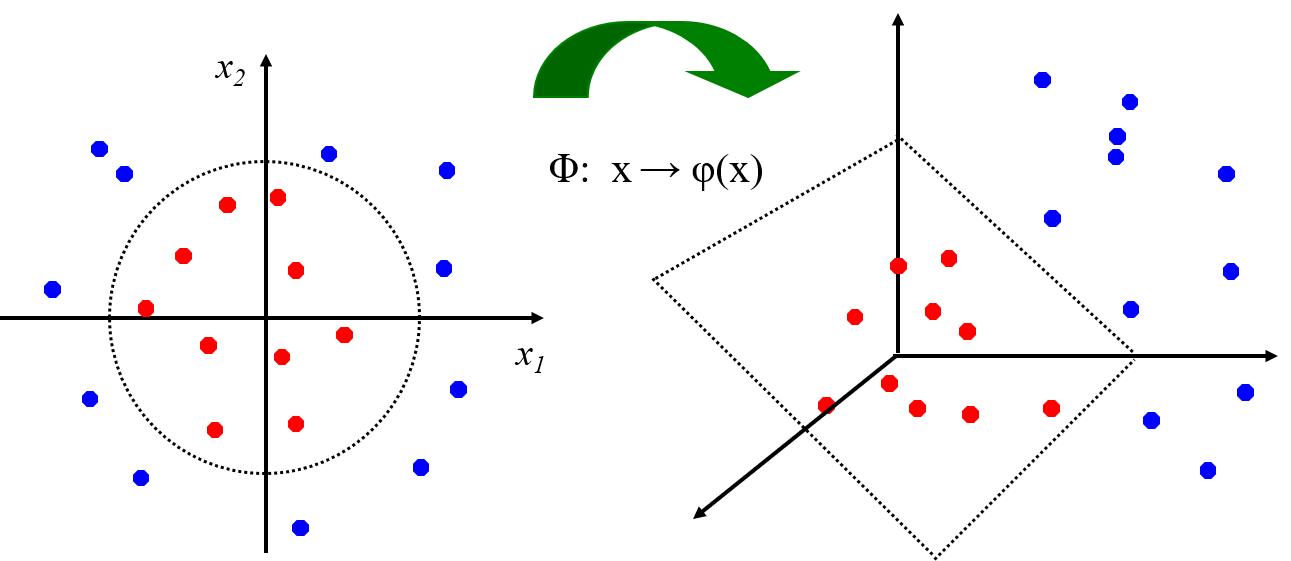
高维空间向量内积运算复杂度高。以二次型为例,直接计算
(x_i⋅x_j⇒Φ(x_i)⋅Φ(x_j)),直接计算的话,复杂度会成倍增加。
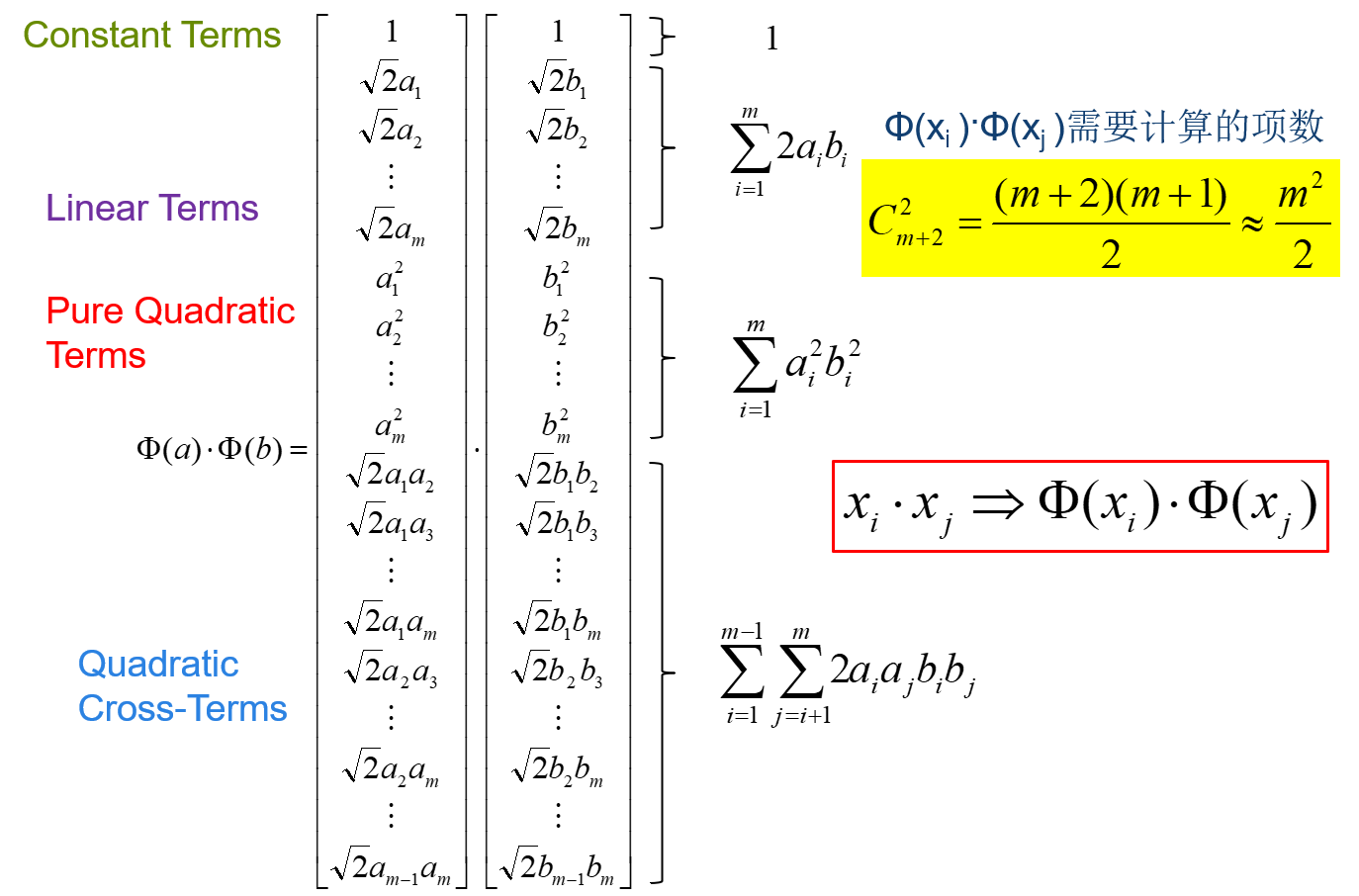
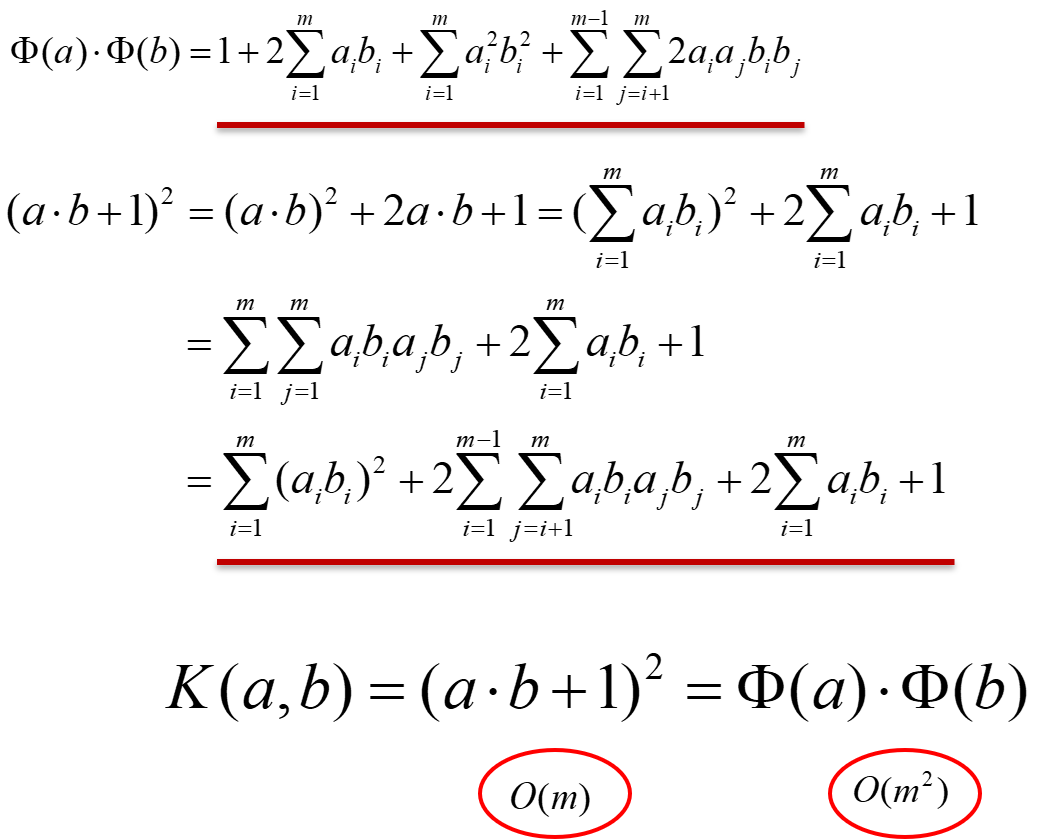
以二次型为例,理解核技巧
通过在低维空间的计算o(m),得到高维空间的结果,不需要知道变换是什么,更不需要变换结果的内积,只需要知道核函数,就可以达到相同的目标。(变换结果的内积)
请看实例,二维空间
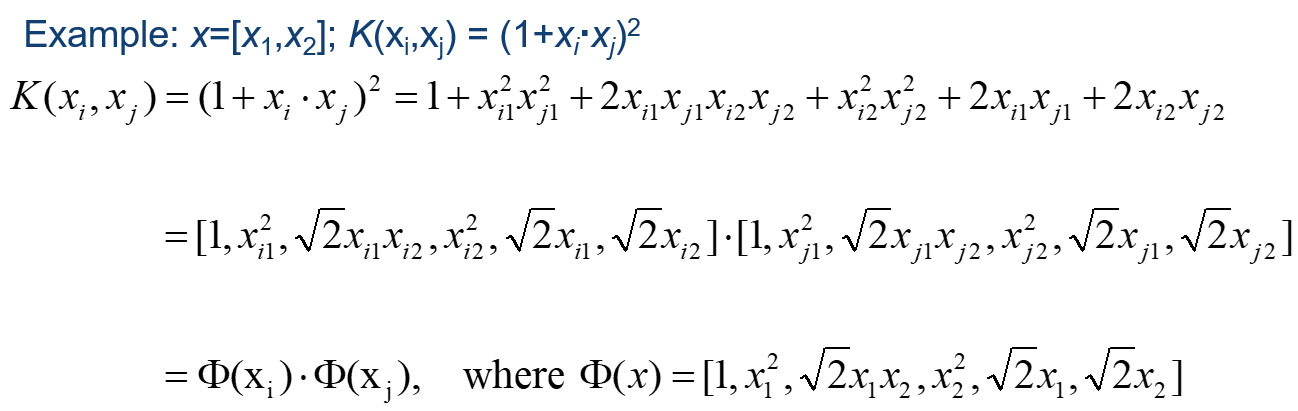
常用的核函数
多项式变换中,当d=2时,就是二次型变换。
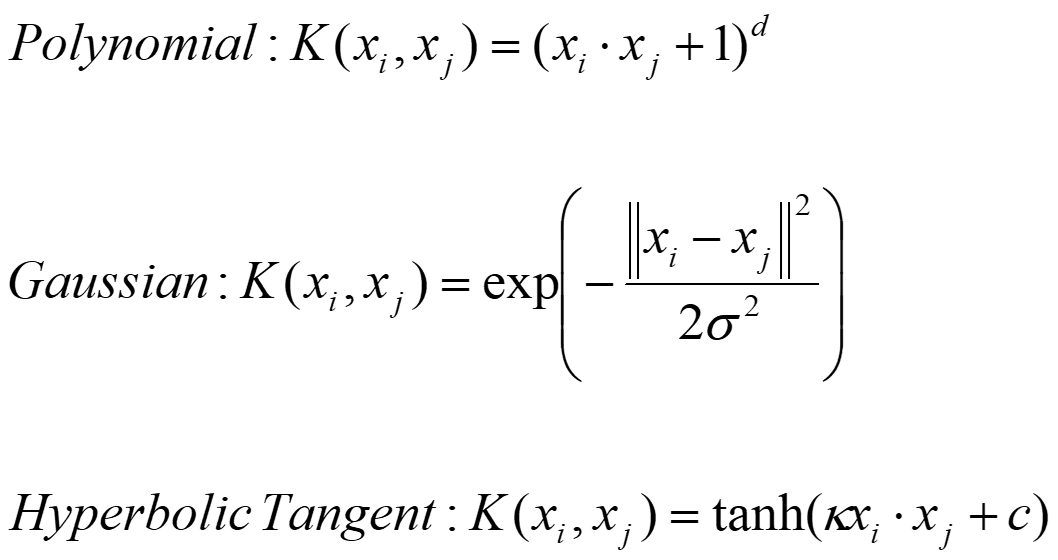
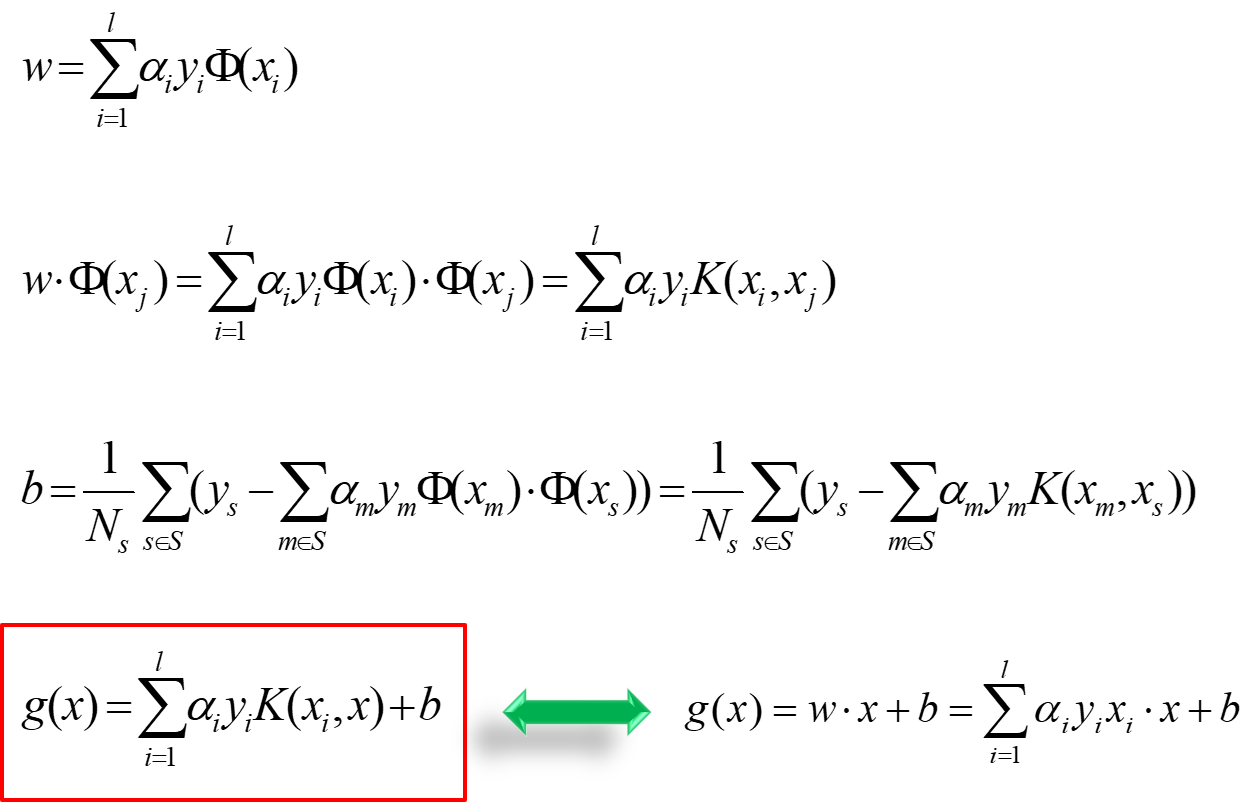
此时w和b的结果如下:
将(x_i)换为(phi(x_i)),将(phi(x_i)cdot phi(x_j))换为(K(x_i,x_j)),其余都不变,真的很简洁。
SVM在Scikit-Learn中的应用
- Linear SVM:(minfrac{1}{2}left|w ight|^2+Csum{zeta^2})
LinearSVC(
penalty='l2',
C=1.0,#就是目标函数的C,C越大(eg:1e9),容错空间越小,越接近硬边界的SVM(最初的SVM,基本不用),C越小(eg:C=0.01),容错空间越大,越接近soft Magin.
)
- 核函数 SVM:
from sklearn.svm import SVC
SVC(
C=1.0,
kernel='rbf',
degree=3,#多项式核函数的指数d
gamma='scale',#高斯基函数中的参数gamma,越大,函数分布越狭窄; gamma越小,决策边界越松弛,当很小时,可以认为趋于无穷大成一条直线了,这时就欠拟合了。gamma取值越大,决策边界越收紧,当很小时,会无限包紧样本点,这时就过拟合了。
)