DFS搜索算法--（1）基础图遍历 绝对看！的！懂！

内容总结 自《啊哈！算法！》

作为一个都大二的了一个菜鸡，做题的时候DFS怎么可以不会呢！！！

作为一个都大二了的（！！！）菜鸡....《啊哈算法》这本书第四章的搜索，开始那里我就没看懂，就跑来看第五章了。结果这个理解起来方便一些....总结摘抄一下给远方的不知名网友and for myself。

以下语言有不严谨之处请多包涵，先理解重要。

深度搜索算法，就是对于一个图（图自己瞎画的  太丑）  如下图所示，给这些圆圈标号。

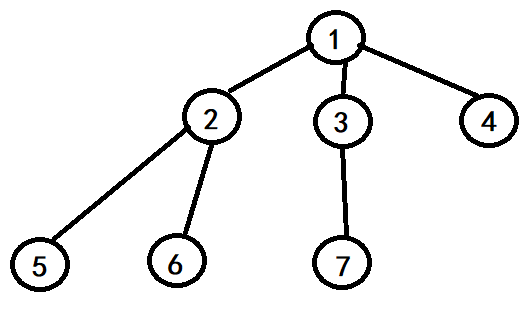
然后我们遍历的时候，是“优先深度” ，先从一条路走到黑走不动了再换条道继续一条路走到黑。即先从1开始，走到2，走到5. 然后走不动了就先回去，先回到2，发现还有6可以走，然后又走到6了。然后又走不动了。便回到2，但是2的所有支路已经都被访问过了，那就再往回走一个，走到1。 回到1以后，2这条道已经走完了，就走到3，再走到7，走不动了再回到3，3没有别的支路可以走了就再回到1，然后再走4

那么上图的访问顺序是（不算重复的顶点）：1  2  5  6  3  7  4

如果一条道走完了，比如说从2走到5，走完了，就要回到上一个路口顶点2。从5到2的过程称为回溯。

那么如何存储一个图呢？我们用一个二维数组arr来存储：

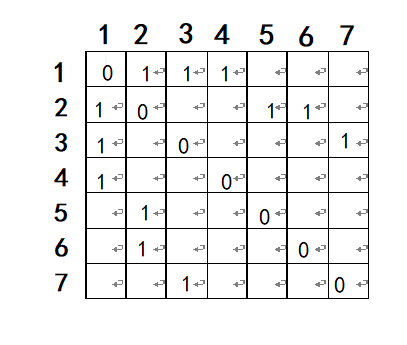
如上两个图所示，二维数组中第i行第j列表示的就是顶点i到顶点j是否有边。1表示有边，空着的就是没有边（在编程时可以将其赋值为9999，画图太麻烦我就省去了） ，二维数组行和列相等的我赋值为0.

能看到，上面的这个图是关于主对角线对称的，这是因为这个图是个‘无向图’。也就是这个图的边没有方向，从1到2和从2到1是一样的，所以 arr[ 2 ] [ 1 ] = arr[ 1 ][ 2 ] = 1。

以下是代码实现：

其中，book[  ]  这个数组一开始全部赋初值为0，表示未被访问过。被访问赋值为1。

还有一个需要知道的小知识点，就是我的代码内又两个return，第一个return表示函数结束，第二个return表示返回上一个dfs()函数，这是递归函数的特殊用法。比如：现在是dfs（5），执行代码时遇到了代码中第二个return，然后就会返回上一个执行的dfs()函数，这就变成了dfs(2)，这个过程就是回溯。

void dfs(int cur)//cur是当前在的顶点的编号
{
    printf("%d ",cur);//按顺序打印出遍历过的点
    sum++;//sum是全局变量，初值为0。每访问一个点，sum++。
    if(sum==n)
        return ;//n为全局变量，是总共点的数量。若sum==n，便是点都访问完了，就退出函数。
    
    for(int i=1;i<=n;i++)//从1号点到n号点依次尝试，看看谁与cur点相连着
    {
        if(arr[cur][i]==1&&book[i]==0)//若这个点没有被访问过并且与cur相连
        {
            book[i]=1;//把这个点标记为已访问
            dfs(i);//递归，继续从这个点再继续深入遍历
        }
    }
    return ;//当与cur相连的所有点都已被访问过了，就返回到上一个dfs（）
}

完整代码如下：

#include<iostream>
#include<cstdio>
using namespace std;

int book[101],sum,n,arr[101][101];

void dfs(int cur)//cur是当前在的顶点的编号
{
    printf("%d ",cur);//按顺序打印出遍历过的点
    sum++;//sum是全局变量，初值为0。每访问一个点，sum++。
    if(sum==n)
        return ;//n为全局变量，是总共点的数量。若sum==n，便是点都访问完了，就退出函数。

    for(int i=1;i<=n;i++)//从1号点到n号点依次尝试，看看谁与cur点相连着
    {
        if(arr[cur][i]==1&&book[i]==0)//若这个点没有被访问过并且与cur相连
        {
            book[i]=1;//把这个点标记为已访问
            dfs(i);//递归，继续从这个点再继续深入遍历
        }
    }
    return ;//当与cur相连的所有点都已被访问过了，就返回到上一个dfs（）
}



int main()
{
    sum=0;
    int m,a,b;
    cin>>n>>m;//m表示有几条边  n表示有几个点
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            if(i==j)
                arr[i][j]=0;
            else
                arr[i][j]=9999999;//把没有边相连的标记为999999
        }
    }

    //读入顶点之间的那些边
    for(int i=0;i<m;i++)
    {
        cin>>a>>b;
        arr[a][b]=1;
        arr[b][a]=1;//由于时无向图，所以两个都要标记。在前面我说过了
    }
    book[1]=1;//从1号顶点出发。标记1号顶点已经被访问
    dfs(1);

    getchar();getchar();


    return 0;
}

ok fine 那么简单图遍历就说完了  下次继续写