最大堆(优先队列)

最大堆（优先队列）

1.它是一颗完全二叉树

2.父节点值大小永远大于子节点的值

用途 用于排序和存储用过的情况

---

知识点1： 二叉树点顺序存储

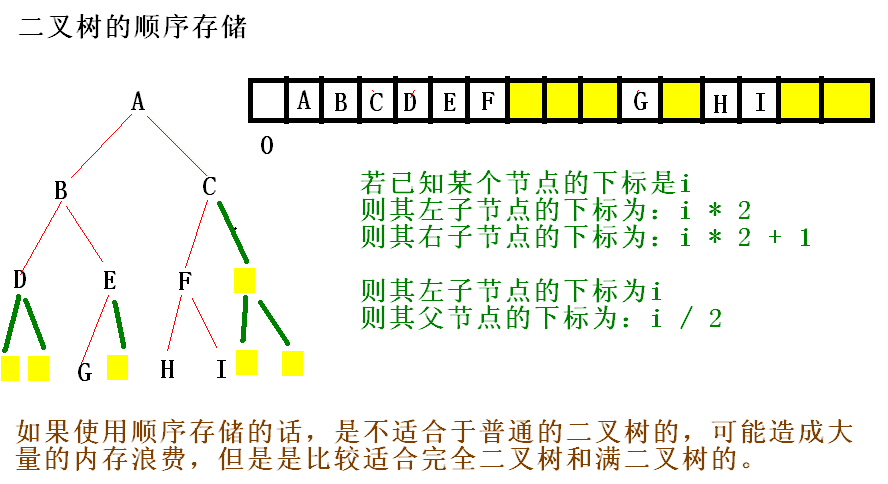
知识点2.完全二叉树

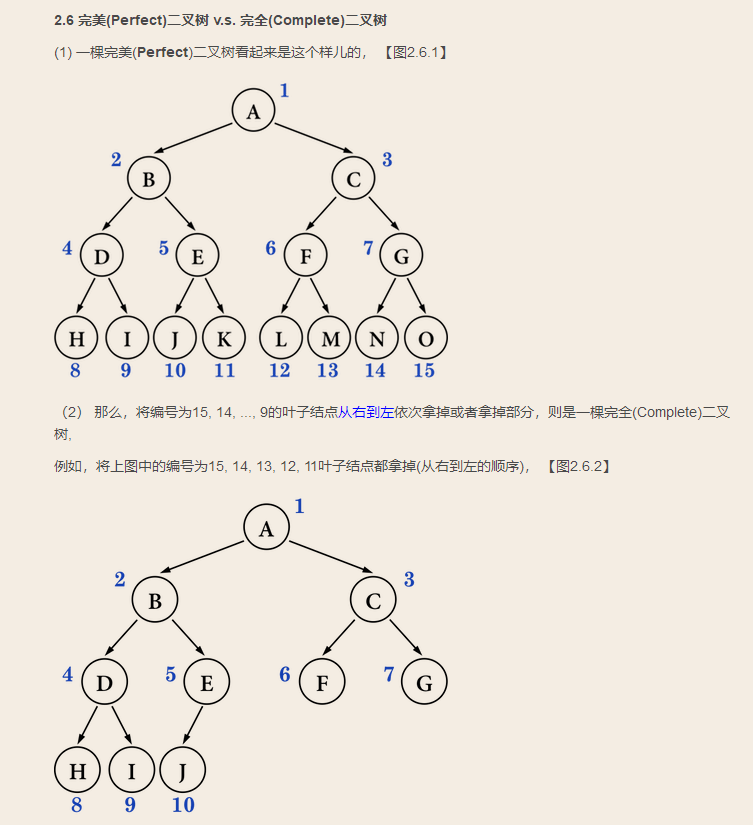
知识点3.最大堆的实现原理

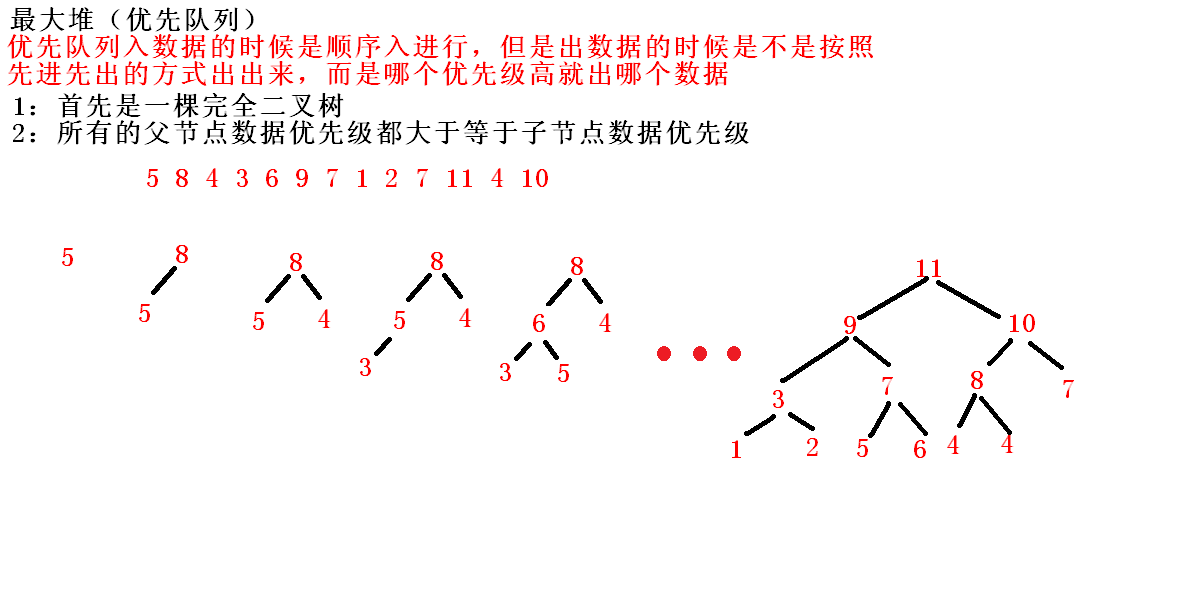
以下就是代码实现部分

/***************************************
作者: 未闻花语
版本: v1.1
最后修改时间: 2018/06/11
电话: 159****7727
功能&使用方法: 
 * 泛型最大堆（优先队列）
 * 1.需要先了解二叉树，完全二叉树
 * 2.了解树形结构的顺序存储
 * 
 * Update:
 *      新增了数目统计属性
 *      修改了Clear函数 数目统计没有归0的问题
 *      删除了多余的引入项
 * 
 * PS：最大堆的2个必要条件
 * 1.一颗完全二叉树
 * 2.所有父节点的值都大于子节点的值
 * 
 * 优点:
 * 1.排序速度极快
 * 2.结构较为简单，由于是完全二叉树，基本没有内存浪费
 * 
 * 
 * 缺点：
 * 
 * 适用：
 *    用于存储和排序共存的结构
 * 
 * 
 * 存在方法：
 * <0> -----> public Push ----- 入
 * <1> -----> public Pop  ----- 出
 * <2> -----> public Clear ---- 清空
 * 
 * 存在属性：
 *      <0> -----> Size ----- 个数
***************************************/
namespace MyHeap
{
    class MaxHeap<T>
    {
        //容量
        int m_capacity;
        //长度
        int m_size;
        //数据
        T[] m_data;
        /*比较函数
         * 参0 > 参1 -----> +1
         * 参0 = 参1 -----> +0
         * 参0 < 参1 -----> -1
         */
        public delegate int Judge(T _t0, T _t1);
        Judge func0;

        //无参构造
        public MaxHeap(Judge _judgeFunc)
        {
            m_size = 0;
            m_capacity = 4;
            m_data = new T[m_capacity];
            func0 = _judgeFunc;
        }

        //带参构造
        public MaxHeap(int _count, Judge _judgeFunc)
        {
            m_size = 0;
            m_capacity = (_count > 1) ? _count : 2;
            m_data = new T[m_capacity];
            func0 = _judgeFunc;
        }

        //扩容
        private void Expansion()
        {
            if (m_size + 1 == m_capacity)
            {
                int nCapacity = (int)(m_capacity * 1.5f);
                T[] nData = new T[nCapacity];
                for (int i = 1; i <= m_size; ++i)
                {
                    nData[i] = m_data[i];
                }

                m_capacity = nCapacity;
                m_data = nData;
            }
        }

        //入堆
        public void Push(T _data)
        {
            Expansion();

            //放入数据
            m_data[++m_size] = _data;

            //向上遍历交换
            int i1 = m_size; //子节点
            int i0 = m_size / 2; //父节点

            while (i1 > 1 && func0(m_data[i0], m_data[i1]) == -1)
            {
                //交换
                T temp = m_data[i0];
                m_data[i0] = m_data[i1];
                m_data[i1] = temp;

                i1 = i0;
                i0 /= 2;
            }
        }

        //出堆
        public T Pop()
        {
            if (m_size < 1)
                return default(T);

            T r = m_data[1];

            //根节点确实的第一次补位操作
            int p = 1;
            while (true)
            {
                int pLeft = 2 * p;
                int pRight = pLeft + 1;

                //有左有右
                if (pRight <= m_size)
                {
                    //比较左右大小
                    if (func0(m_data[pLeft], m_data[pRight]) >= 0)
                    {
                        m_data[p] = m_data[pLeft];
                        p = pLeft;
                    }
                    else
                    {
                        m_data[p] = m_data[pRight];
                        p = pRight;
                    }
                }
                //有左无右
                else if (pLeft <= m_size)
                {
                    m_data[p] = m_data[pLeft];
                    p = pLeft;
                    break;
                }
                //无左无右
                else
                    break;
            }

            //为了完全二叉树的第二次补位操作
            m_data[p] = m_data[m_size];
            while (p > 2 && func0(m_data[p / 2], m_data[p]) == -1)
            {
                //交换
                T temp = m_data[p / 2];
                m_data[p / 2] = m_data[p];
                m_data[p] = temp;

                p /= 2;
            }

            m_size--;

            return r;
        }

        //清空
        public void Clear()
        {
            while (m_size > 0)
            {
                Pop();
            }
            m_size = 0;
        }

        //存在元素个数
        public int Size
        {
            get { return m_size; }
        }
    }
}

以下是 入口点测试部分

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
//包含命名空间 
using MyHeap;
namespace DataStructure
{
    class Program
    {
        static void Main(string[] args)
        {
            string[] rNameSpace = new string[] {"蒋伟","吴悦","曾真","刘芸",
            "珠海妮","李小满","薛涵","邱伊雨","李晶晶","戴林江","代安东","黄挺",
                "陈政","叶小青","徐逸"};
            var team0 = new MaxHeap<Student>(JudgeFunc);
            team0.Push(new Student(25, "李晶晶", true));
            team0.Push(new Student(18, "薛涵", true));
            team0.Push(new Student(15, "代安东", false));
            team0.Push(new Student(23, "李小满", true));
            team0.Push(new Student(10, "蒋伟", false));

            for (int i = 0; i < 5; ++i)
                Console.WriteLine(team0.Pop().ToString());
            
        }
        static int JudgeFunc(Student _s0, Student _s1)
        {
            if (_s0.m_id == _s1.m_id)
                return 0;
            else if (_s0.m_id > _s1.m_id)
                return 1;
            else
                return -1;
        }

    }
    class Student
    {
        //学号
        public int m_id;
        //姓名
        public string m_name;
        //性别
        public bool m_isGirl;
        //构造
        public Student(int _id, string _name, bool _isGirl)
        {
            m_id = _id;
            m_name = _name;
            m_isGirl = _isGirl;
        }

        //重写打印函数
        public override string ToString()
        {
            return string.Format("{0}[{1}] - {2}", m_name, m_id, m_isGirl ? "Girl" : "Boy");
        }
    }
}

以下是输出结果

再进行一个与冒泡排序的速度比较

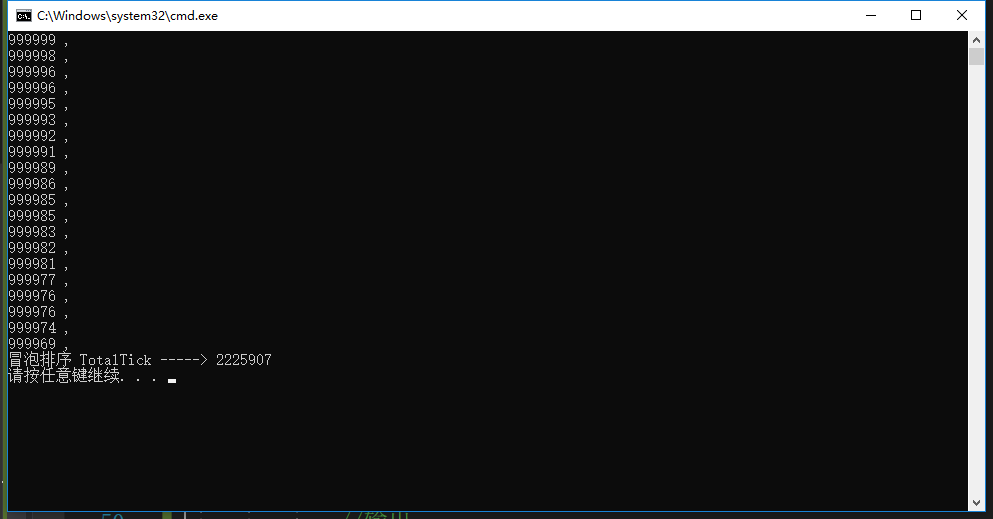
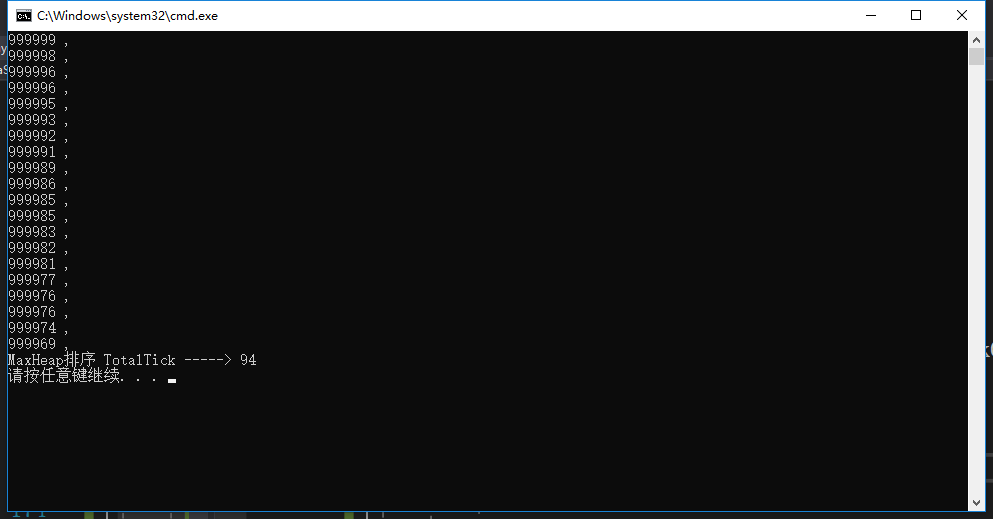
从上述比较看出 当排序数组为100W时 最大堆的速度是冒泡排序的2W3多倍，上述证明了再设计程序时选择数据结构的重要性！

附上比较算法

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
//包含命名空间 
using MyHeap;
//引用动态库

namespace DataStructure
{
    class Program
    {
        static void Main(string[] args)
        {
            //随机值
          
            const int NumCount = 1000000;
            int[] rNum = new int[NumCount];
            Random ra = new Random(6);
            for (int i = 0; i < NumCount; ++i)
                rNum[i] = ra.Next(0, NumCount);
            int startTick = System.Environment.TickCount;

            //最大堆排序
            var team0 = new MaxHeap<int>(JudgeFunc);
            for (int i = 0; i < NumCount; ++i)
                team0.Push(rNum[i]);

            //输出
            for (int i = 0; i < 20; ++i)
                Console.WriteLine(team0.Pop() + " , ");

            Console.WriteLine("MaxHeap排序 TotalTick -----> " + (System.Environment.TickCount - startTick));

            ////冒泡排序
            //for (int i = 0; i < NumCount; ++i)
            //{
            //    for (int j = NumCount - 1; j > i; --j)
            //    {
            //        if (rNum[i] < rNum[j])
            //        {
            //            var temp = rNum[i];
            //            rNum[i] = rNum[j];
            //            rNum[j] = temp;
            //        }
            //    }
            //}

            ////输出
            //for (int i = 0; i < 20; ++i)
            //    Console.WriteLine(rNum[i] + " , ");

            //Console.WriteLine("冒泡排序 TotalTick -----> " + (System.Environment.TickCount - startTick));


        }
        static int JudgeFunc(int _s0, int _s1)
        {
            if (_s0 == _s1)
                return 0;
            else if (_s0 > _s1)
                return 1;
            else
                return -1;
        }

    }
    class Student
    {
        //学号
        public int m_id;
        //姓名
        public string m_name;
        //性别
        public bool m_isGirl;
        //构造
        public Student(int _id, string _name, bool _isGirl)
        {
            m_id = _id;
            m_name = _name;
            m_isGirl = _isGirl;
        }

        //重写打印函数
        public override string ToString()
        {
            return string.Format("{0}[{1}] - {2}", m_name, m_id, m_isGirl ? "Girl" : "Boy");
        }
    }
}