BZOJ2658-[Zjoi2012]小蓝的好友
题意:

题解:
我们可以求出不含任何资源点的矩形的数量,然后用总矩形数减去这个值就是答案。
首先我们从上往下枚举每一行,来求底部为当前行的矩形数量。然后我们可以维护当前行的每一个点向上最多能延伸多少长。
然后假设当前状态是这样的(图是从其他人的blog里找到的):
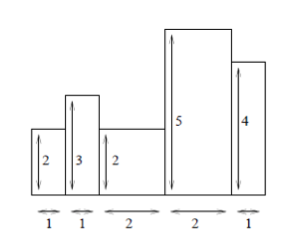
然后我们可以把这个图划分一下:
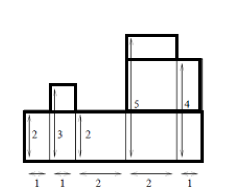
可以发现所有符合我们要求的矩形的左上角和右上角都在同一个矩形中,然后对于每个矩形统计答案就可以了。
然后我们就要想办法维护每个矩形。
我们可以对于当前行每一列最多能向上延伸的距离建一棵笛卡尔树。
然后我们可以发现,对于每个节点,它代表的矩形的宽度就是它的size,而矩形的高度就是它能向上延伸的距离减去它的父节点能向上延伸的距离。
然后对于每个节点维护一下能向上延伸的最大距离、它的size和它的子树的答案和。
对于每次枚举到下一行的时候,我们先将根节点打一个距离+1的tag。
然后对于该行的每一个资源点,我们都可以将它代表的节点的距离设为0。
由于要满足笛卡尔树的性质,我们要先把这个点旋到根,然后将距离设为0。旋到根的方法和treap是一样的。
然后我们就可以统计出答案了。
由于数据是随机的,所以树的深度是log级别的,复杂度是对的。
#include<cstdio> #include<vector> typedef long long ll; using namespace std; const int maxn=40000; int n,r,c,rt; ll ans; vector<int> g[maxn+10]; struct node{ int ch[2],sz,ht,tag; ll val; }a[maxn+10]; void apply(int p,int v){ a[p].tag+=v; a[p].ht+=v; } void update(int p){ a[p].sz=1; a[p].val=0; for(int i=0;i<=1;++i){ a[p].sz+=a[a[p].ch[i]].sz; a[p].val+=a[a[p].ch[i]].val+1ll*a[a[p].ch[i]].sz*(a[a[p].ch[i]].sz+1)*(a[a[p].ch[i]].ht-a[p].ht)/2; } } int build_tree(int l,int r){ if(l>r) return 0; int mid=l+r>>1; a[mid].ch[0]=build_tree(l,mid-1); a[mid].ch[1]=build_tree(mid+1,r); update(mid); return mid; } void push_down(int p){ for(int i=0;i<=1;++i) if(a[p].ch[i]) apply(a[p].ch[i],a[p].tag); a[p].tag=0; } void rotate(int &p,int d){ int q=a[p].ch[d]; a[p].ch[d]=a[q].ch[d^1]; a[q].ch[d^1]=p; update(p); update(q); p=q; } void change(int &p,int k){ push_down(p); if(k==a[a[p].ch[0]].sz+1){ a[p].ht=0; update(p); return; }else if(k<=a[a[p].ch[0]].sz){ change(a[p].ch[0],k); rotate(p,0); }else{ change(a[p].ch[1],k-a[a[p].ch[0]].sz-1); rotate(p,1); } } int main(){ scanf("%d%d%d",&r,&c,&n); for(int i=1;i<=n;++i){ int x,y; scanf("%d%d",&x,&y); g[x].push_back(y); } ans=1ll*r*(r+1)*c*(c+1)/4; rt=build_tree(1,c); for(int i=1;i<=r;++i){ apply(rt,1); for(int j=0;j<g[i].size();++j) change(rt,g[i][j]); ans-=a[rt].val+1ll*a[rt].sz*(a[rt].sz+1)*a[rt].ht/2; } printf("%lld",ans); return 0; }