《数据结构》--第七章小结--查找
一、基本概念
查找表:是由同一类型的数据元素(或记录)构成的集合。查找表分为静态查找表和动态查找表。
关键字(Key):是数据元素中某个数据项的值,又称为键值,用它可以标识一个数据元素。若关键字可以唯一地标识一个记录,则称此关键字为主关键字(Primary Key);若关键字对应多个记录,则称此关键字为次关键字(Secondary Key)。
关键码:主关键字对应的数据项称为主关键码;次关键字对应的数据项称为次关键码。
查找:就是根据给定的某个值,在查找表中确定一个其关键字等于给定值的数据元素(或记录)。
静态查找表:只做查找操作的查找表。主要操作有:
1)查询某个“特定的”数据元素是否在查找表中;
2)查询某个“特定的”数据元素的各种属性(值)。
动态查找表(Dynamic Search Table):在查找的过程中同时插入查找表中不存在的数据元素,或者从查找表中删除已经存在的某个数据元素。主要操作有:
1)查找时插入数据元素;
2)查找时删除数据元素。
查找结构:面向查找操作的数据结构。
1)对于静态查找表,一般考虑使用线性表结构来组织数据;对应查找方法有:顺序表使用顺序查找(线性查找);有序表使用折半查找、插值查找、斐波那契查找。
2)对于动态查找表,一般考虑二叉树结构来组织数据;对应查找方法有:二叉排序树、平衡二叉树、B树。
3)散列表查找(哈希表查找)比较常用。
二、查找算法
1. 顺序查找
顺序查找适合于存储结构为顺序存储或链接存储的线性表。
2. 二分查找
元素必须是有序的,如果是无序的则要先进行排序操作。
二分查找即折半查找,属于有序查找算法。用给定值value与中间结点mid的关键字比较,若相等则查找成功;若不相等,再根据value与该中间结点关键字的比较结果确定下一步查找的子表
将数组的查找过程绘制成一棵二叉树排序树,如果查找的关键字不是中间记录的话,折半查找等于是把静态有序查找表分成了两棵子树,即查找结果只需要找其中的一半数据记录即可,等于工作量少了一半,然后继续折半查找,效率高。
时间复杂度为O(log2n);
折半计算mid的公式
mid = (low+high)/2;
if(a[mid]==value)
return mid;
if(a[mid]>value)
high = mid-1;
if(a[mid]<value)
low = mid+1;
3. 插值查找
改进二分查找算法,将查找点的选择改进为自适应选择,差值查找也属于有序查找。
对于表长较大,而关键字分布又比较均匀的查找表来说,插值查找算法的平均性能比折半查找要好的多。反之,数组中如果分布非常不均匀,那么插值查找未必是很合适的选择。
折半计算mid的公式,等式变换后得到: mid = (low+high)/2 = low + (high-low)/2
mid等于最低下标low加上最高下标high与low的差的一半。将这个 1/2 进行改进,通过类比,改进为下面的计算方案:
mid = low + ((key - a[low])/(a[high] - a[low]))(high - low)这样就可以大大提高查找的效率。
4. 斐波那契查找
改进二分查找算法,通过运用黄金比例选择查找点进行查找,同样地,斐波那契查找也属于一种有序查找算法。
斐波那契查找的时间复杂也为O(logn),但就平均性能来说,斐波那契查找要优于折半查找。可惜如果是最坏情况,比如这里key=l,那么始终都处于左侧长半区在查找,则查找效率要低于折半查找。
复杂度也为O(log2n)
5. 分块查找
分块查找的平均查找长度ASL是折半查找的平均查找长度加顺序查找块内平均查找长度
6. 树表查找
如果查找的数据集是有序线性表,并且是顺序存储的,查找可以用折半、插值、斐波那契等查找算法来实现,可惜,因为有序,在插入和删除操作上,就需要耗费大量的时间
若查找表无序,则插入删除可无需移动大量记录,但于查找不利。因此这里一种即可以使得插入和删除效率不错,又可以比较高效率地实现查找的算法。
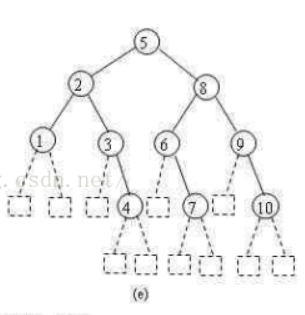
二叉排序树(Binary Sort Tree),又称为二叉查找树。它或者是一棵空树,或者是具有下列性质的二叉树。
若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
若它的右子树不空 ,则右子树上所有结点的值均大于它的根结点的值;
它的左、右子树也分别为二叉排序树。
平衡二叉树(AVL树)
平衡二叉树,是一种二叉排序树,其中每一个节点的左子树和右子树的高度差至多等于1。
从平衡二叉的英文名字(AVL树),你也可以体会到,它是一种高度平衡的二叉排序树。
高度平衡意思是说,要么它是一棵空树,要么它的左子树和右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。
B-树
B树可以看作是对查找树的一种扩展,即他允许每个节点有M-1个子节点。
-
根节点至少有两个子节点
-
每个节点有M-1个key,并且以升序排列
-
位于M-1和M key的子节点的值位于M-1 和M key对应的Value之间
-
其它节点至少有M/2个子节点
下图是一个M=4 阶的B树:

B+树
B+树是对B树的一种变形树,它与B树的差异在于:
- 有k个子结点的结点必然有k个关键码;
- 非叶结点仅具有索引作用,跟记录有关的信息均存放在叶结点中。
- 树的所有叶结点构成一个有序链表,可以按照关键码排序的次序遍历全部记录。
如下图,是一个B+树:

三、实践
7-1 QQ帐户的申请与登陆 (30 分) 实现QQ新帐户申请和老帐户登陆的简化版功能。最大挑战是:据说现在的QQ号码已经有10位数了。 输入格式: 输入首先给出一个正整数N(≤10 5 ),随后给出N行指令。每行指令的格式为:“命令符(空格)QQ号码(空格)密码”。其中命令符为“N”(代表New)时表示要新申请一个QQ号,后面是新帐户的号码和密码;命令符为“L”(代表Login)时表示是老帐户登陆,后面是登陆信息。QQ号码为一个不超过10位、但大于1000(据说QQ老总的号码是1001)的整数。密码为不小于6位、不超过16位、且不包含空格的字符串。 输出格式: 针对每条指令,给出相应的信息: 1)若新申请帐户成功,则输出“New: OK”; 2)若新申请的号码已经存在,则输出“ERROR: Exist”; 3)若老帐户登陆成功,则输出“Login: OK”; 4)若老帐户QQ号码不存在,则输出“ERROR: Not Exist”; 5)若老帐户密码错误,则输出“ERROR: Wrong PW”。 输入样例: 5 L 1234567890 myQQ@qq.com N 1234567890 myQQ@qq.com N 1234567890 myQQ@qq.com L 1234567890 myQQ@qq L 1234567890 myQQ@qq.com 输出样例: ERROR: Not Exist New: OK ERROR: Exist ERROR: Wrong PW Login: OK
AC代码:

#include <iostream> #include <cstring> #include <map> using namespace std; map<string,string> Q;//用map的方法 int main() { int m; cin>>m; string a3,a2; char a1; while(m--) { cin>>a1>>a2>>a3; if(a1=='N') { if(Q.find(a2)==Q.end())//查找到迭代器的最后,若无则为新 { Q[a2]=a3; cout<<"New: OK"<<endl; } else { cout<<"ERROR: Exist"<<endl; } } if(a1=='L') { if(Q.find(a2)==Q.end()) { cout<<"ERROR: Not Exist"<<endl; } else { map<string,string>::iterator it;//find()函数返回一个迭代器指向键值为key的元素,如果没找到就返回指向map尾部的迭代器 it=Q.find(a2); if(it->second==a3) { cout<<"Login: OK"<<endl; } else { cout<<"ERROR: Wrong PW"<<endl; } } } } return 0; }
其实,在写这道题时我是想开辟数组的,然后我意识到,如果开辟数组我就会内存爆炸,肯定行不通的。所以我就开始寻找其他方法,例如本章的方法。然后我就想到了哈希表,发现这个结构好像刚刚好适合这个题的。然后我就去查书和资料,然后查得到一个map函数的有意思的方法。以上代码用map函数,就很舒服。附上参考链接:https://blog.csdn.net/YC1101/article/details/79311029
三、总结
上一次的目标基本达成,还顺带学习了一下map的用法,
下一阶段的目标:备考准备,好好复习。
期末噶油!
