CF1016C Vasya And The Mushrooms 题解

这道题一眼就是一个DP（大雾），但题目中有一句很有趣的话

“He wants to visit all the cells exactly once and maximize the total weight of the collected mushrooms.”

也就是每个格子必须且只能经过一次，而且只有两派格子，所以是不是一目了然的只有两种行走路线。

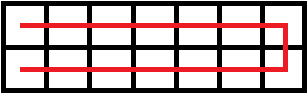
其实不然，你还可以这么走

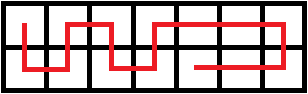或者，这么走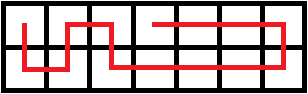

也就是把前两种行走方式结合一下

                      

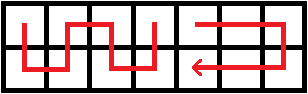
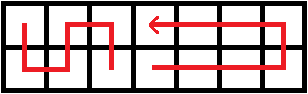
不过也没有变得不可做，因为一定是先用第一种行走方式，再接第二种；不可能存在先走第二种，再第一种的情况（都已经拐回去了，还走啥啊）。所以枚举一下从何时开始更换行走方式即可。这两种行走方式吃到的蘑菇都可以先预处理出来。

a1是第一行的蘑菇生长率，a2是第二行的

因为观察到无论从何时改变行走方式，都可以看成是在走完一个整列后再改变，所以所有的数组都是以列数作为下标的。

首先预处理蛇形行走方式：

两行两行处理，每次走一个U型，要注意蘑菇不是从第1秒开始长的（其实是时间是从 0 s 开始记的，不过一样哈）

init_b(){
    //b[i]表示蛇形在取完第i列的格子的蘑菇后的 
    //第一个格子为第1s(但不吃蘑菇)
    //这个格子蘑菇数为(i-1)*a 
    int s=0;
    for(int i=1;i<=n;i+=2){
        s+=a1[i]*(i*2-2);
        s+=a2[i]*(i*2-1);
        b[i]=s;
        s+=a2[i+1]*(i*2);
        s+=a1[i+1]*(i*2+1);
        b[i+1]=s;
        //走了一个U型 ↓→↑
    }//走了一个S型 
}

再预处理环形行走方式：

这样的一条路可以看成是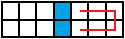的一条路加上蓝色的两个格子的蘑菇。

不过原来路上的每只蘑菇都多生长了 1 s，所以要加一个“后缀和”。

init_S(){
    //S[i]表示从第i列(从左往右数)以及右边的半圈的蘑菇生长率之和 
    int s=0;
    for(int i=n;i>=1;i--)
    s+=a1[i]+a2[i],S[n-i+1]=s;
}

如果是从上绕到下，上面的格子生长时间是0s（还没有开始长，也不用加），下面的格子生长时间是后面的两列格子数+上面的一个格子=（l*2+1），l 是后面的长度；

如果是从下绕到上，相反就好了（没人会告诉你还有一个东西叫复制粘贴）

init_C1(){
    //从上面绕下去
    //c1[i]表示从第i列(从左往右数)开始的 
    int s=0;
    for(int i=n,l=0;i>=1;i--,l++){
        s+=S[l];
        s+=a2[n-l]*(l+l+1);
        c1[i]=s;
    } 
//    for(int i=1;i<=n;i++)
//    cout<<c1[i]<<" ";
}

init_C2(){
    //从下面绕上去
    //c2[i]表示从第i列(从左往右数)开始的 
    int s=0;
    for(int i=n,l=0;i>=1;i--,l++){
        s+=S[l];
        s+=a1[n-l]*(l+l+1);//只有这里的a1,a2换了一下 
        c2[i]=s;
    } 
//    for(int i=1;i<=n;i++)
//    cout<<c2[i]<<" ";
}

最后是统计答案（程序主体）：

经过观察，我们发现，从上往下绕，只能发生在走完偶数列格子后（一开始就开始绕可以看成是从第0列就开始拐弯），因为只有这时最后一步才踩在上面一行格子上。

而从下往上绕，只能在走过奇数列格子后，这时落脚在下面一行，可以开始从下往上绕。

因为在绕之前已经经过了i列（2*i个格子），所以后面绕的所有格子都多生长了2*i秒，再加上这些后缀和*生长时间 就是这么走一趟的收获了。与答案求max。

//枚举从哪开始拐，上拐下拐 
    for(int i=0;i<=n;i++){
        //从下一列开始拐弯 
        if(i%2) ans=max(ans,b[i]+c2[i+1]+S[n-i]*(i*2));
        else    ans=max(ans,b[i]+c1[i+1]+S[n-i]*(i*2));
    }

就结束了。

下面贴上完整简洁（压行）版代码

#include<iostream>
#include<cstdio>
#define N 300100
#define int long long
using namespace std;
int n,ans,a1[N],a2[N],S[N],b[N],c1[N],c2[N];
init_S(){
    int s=0;
    for(int i=n;i>=1;i--)
    s+=a1[i]+a2[i],S[n-i+1]=s;
}
init_b(){
    int s=0;
    for(int i=1;i<=n;i+=2){
        s+=a1[i]*(i*2-2);
        s+=a2[i]*(i*2-1);
        b[i]=s;
        s+=a2[i+1]*(i*2);
        s+=a1[i+1]*(i*2+1);
        b[i+1]=s;
    }
}
init_C1(){
    int s=0;
    for(int i=n,l=0;i>=1;i--,l++){
        s+=S[l];s+=a2[n-l]*(l+l+1);
        c1[i]=s;
    }
}
init_C2(){
    int s=0;
    for(int i=n,l=0;i>=1;i--,l++){
        s+=S[l];s+=a1[n-l]*(l+l+1);
        c2[i]=s;
    }
}
signed main(){
    cin>>n;
    for(int i=1;i<=n;i++)cin>>a1[i];
    for(int i=1;i<=n;i++)cin>>a2[i];
    init_S(); 
    init_b(); 
    init_C1();
    init_C2();
    for(int i=0;i<=n;i++){
        if(i%2) ans=max(ans,b[i]+c2[i+1]+S[n-i]*(i*2));
        else    ans=max(ans,b[i]+c1[i+1]+S[n-i]*(i*2));
    }
    cout<<ans;
}