词法分析（五）：正规式与有限自动机

词法分析概述

---

唉，不想学习，老是想起别的事情

---

这篇博客讲的是正规式和有限自动机的等价性，
为NFA写出等价的正规式，为一个正规式构造等价的NFA

有了NFA与正规式的关系，就把正规式和前面所述串接起来了
总而言之，状态图，正规式/正规集，有限自动机都是同种东西的不同形式
正规集是实在存在的编程语言的单词集合，正规式是单词集合的抽象描述，
计算机难以理解正规式，或者说正规式的概念难以映射到计算机上，
所以借助有限自动机实现正规式，而有限自动机又可以用状态转移图形象地描述出来
go

---

正规式与有限自动机的等价性

正规式 r 与有限自动机 M 等价：L(r） = L(M)，正规式对应的正规集与FA识别的字的全体是相等的

定理：对任何FA M，都存在一个正规式 r，使得L(r）= L(M)
定理：对于任何正规式 r，都存在一个FA M，使得L(M)=L(r）

---

为NFA构造正规式

广义的状态转换图，弧上可以是正规式
对待任何NFA M，在状态转换图上加进新的初态X，用 ε弧 连接原先的初态；
添加新的终态结点Y，用 ε弧 将原先的终态与Y连接

（改造后的NFA只有一个初态和一个终态，最后构造出的正规式也会合并为一个）

使用一下三条规则，逐步消去结点，直到只剩下X、Y结点

• 串联
  
• 并联
  
• 重复
  

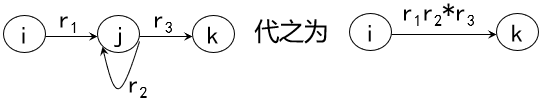
不难看出，以上变换都是等价变换
最后，X到Y的弧上的正规式就是与该FA等价的正规式

以下图为例



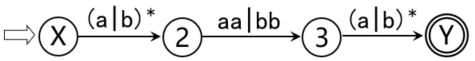
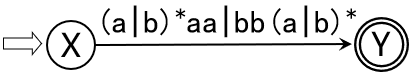
通过不断合并、减少结点，可以把NFA变成正规式，图中NFA的正规式即为 (a|b)*aa|bb(a|b)*

为什么FA弧上可以是正规式？
因为正规式和FA（NFA（DFA））是等价概念，弧上的正规式即是一个FA，
作为整个FA的一个子状态机（像是一种简写）

---

构造正规式时要注意变换次序

---

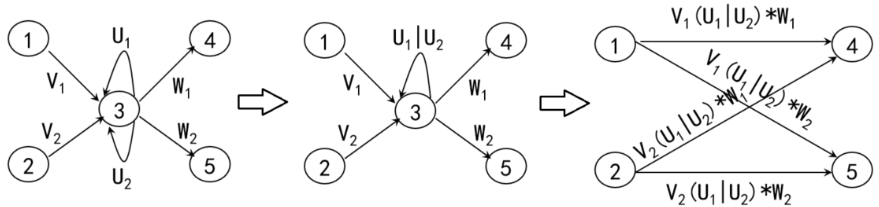
任意正规式存在等价的NFA

这里有一个更严格的定理
对于 Σ 上的正规式 r，都存在一个NFA M，使L(M)=L(r），
并且 M 只有一个初态和一个终态，且没有从终态出发的弧

这个定理更加严苛，证明了这个定理，即证明了前述定理

下面给出一个严格的数学证明

对给定正规式r中的运算符数目进行归纳

• 验证 r 中的运算符数目为0时，结论成立
• 假设结论对于运算符数目少于 k(k>=1) 的正规式成立
• 基于该假设，证明结论对于运算符数目为 k 的正规式成立

若 r 具有零个运算符，则 r=ε 或 r=∅ 或 r=a，其中a∈Σ
证明：
 分别为 r=ε、r=∅、r=a 构造NFA如下图，

可以看出构造出的NFA均只有一个初态和一个终态，且没有从终态出发的弧
证毕

假设结论对于运算符数目少于 k(k>=1) 的正规式成立，证明结论对于运算符数目为 k 的正规式成立
证明：
 当 r 中含有 k 个运算符时，r 有三种情况

1. r = r₁|r₂
2. r = r₁·r₂
3. r = r₁^*

分别对这三种情况进行证明

• 当 r = r₁|r₂ 时，r₁ 和 r₂ 中的运算符数目均少于k，由假设知，存在 M_i = < S_i，Σ_i，δ_i，q_i，{f_i} >，
  使得L(M_i)=L(r_i)，并且M_i没有从终态触发的弧，q_i、f_i分别为其唯一的初态和终态（这里 i = 1,2）
  令 S₁∩S₂=∅，在 S₁∪S₂ 中加入两个新的状态q₀，f₀，构造NFA如下
  
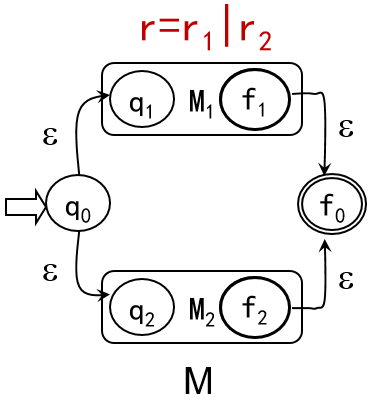
  M₁、M₂ 分别为 r₁、r₂ 等价的NFA，用 ε弧 连接 q₀ 与 q₁、q₂ 和 f₁、f₂ 与 f₀，
  （ 用 ε弧 将NFA的终态与其他NFA的初态或新的终态连接，或者连接新的初态和子NFA的初态，
  由于 ε弧 不会改变一条通路上所识别的字，因此这种方法常用来构造新的NFA）
  新产生的 M = <S₁∪S₂∪{q₀,f₀}，Σ₁∪Σ₂，δ，q₀，f₀>，其中 δ 的定义如下：
  
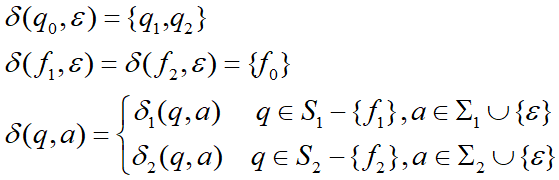
  M的状态转换函数 δ 即是包含 q₀ 到 q₁、q₂ 的弧，包含 f₁、f₂ 到 f₀ 的弧，
  且包括 M₁ 内部的 δ₁，包括 M₂ 内部的 δ₂

这样构造的NFA M 就把 M₁ 和 M₂ 并联起来，
L(M) = L(M₁) ∪ L(M₂) = L(r₁) ∪ L(r₂) = L(r₁|r₂) = L(r）
 

• 当 r = r₁·r₂ 时，同理，有分别与 r₁ 和 r₂ 等价的 M₁ 与 M₂，
  将 f₁ 与 q₂ 用 ε弧 连接，状态图如下
  
  新构造的NFA M = < S₁∪S₂，Σ₁∪Σ₂，δ，q₀，{f₀} >，其中 δ 为
  

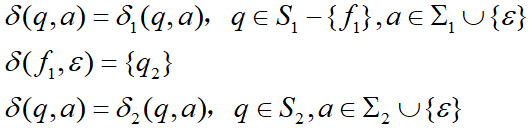
这样构造的NFA M 就把 M₁ 和 M₂ 串联起来，
L(M) = L(M₁)L(M₂) = L(r₁)L(r₂) = L(r₁·r₂) = L(r）
 

• 当 r = r₁^* 时，同理，有与 r₁ 等价的NFA M₁ = <S₁，Σ₁，δ₁，q₁，{f₁}>，
  添加新的初态 q₀，新的终态 f₀
  将 q₀ 、f₁ 分别与 q₁、f₀ 用 ε弧 连接，状态图如下
  
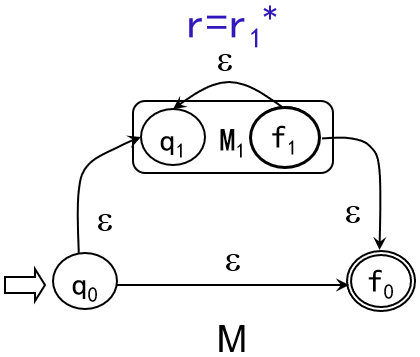
  新构造的NFA M = <S₁∪{q₀,f₀}，Σ₁，δ，q₀，{f₀}>，其中 δ 为
  

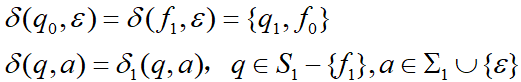
这样构造的NFA M 就实现了 M₁ 的任意次重复
L(M) = L(M₁)^* = L(r₁)^* = L(r₁^*) = L(r）

证毕

若对于运算符数目少于 k(k>=1) 的正规式，都有等价的NFA，
则运算符数目等于 k 的正规式也存在等价的NFA；
又运算符数目为零的正规式具有等价的NFA，
所以含有任意个运算符的正规式，都可以构造出等价的NFA

证毕

---

为正规式构造NFA

上述证明的过程实质上是一个将正规表达式转换为有限自动机的算法

有正规式 r，构造 Σ 上的NFA M’，使L(M’) = L(r）
首先，把 r 表示成

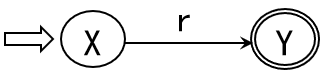
然后按一下规则对 r 进行拆分

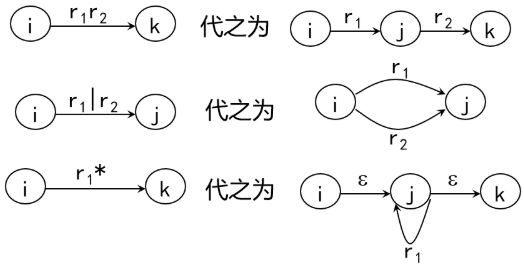
逐步把状态图转变为每条弧接受的是 Σ 上的一个字符或ε，最后得到一个NFA M’，显然 L(M’) = L(r）

---

小结：有了正规式与NFA的等价转换关系，就可以由一个程序设计语言的正规集得到正规式，
再将正规式转换为等价的NFA，接着用子集法将NFA确定化，可以进一步将得到的DFA最小化，
再进行程序实现

---

2019/7/24