哈夫曼树
哈夫曼树即最优二叉树,算法如下:
(1)在当前未使用结点中找出两个权重最小的作为左右孩子,计算出新的根结点
(2)新的根结点继续参与过程(1),直至所有结点连接为一棵树
如下图,symbol为具体字符,Frequency为出现频率(权重)
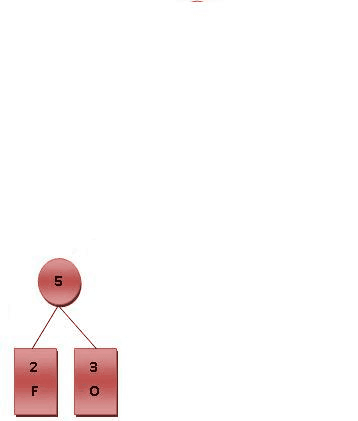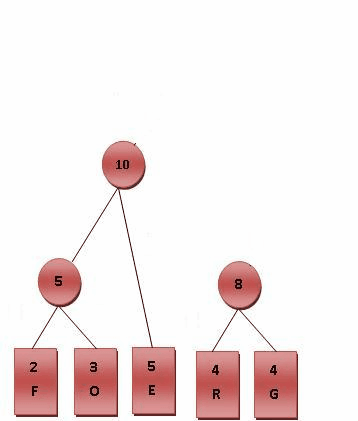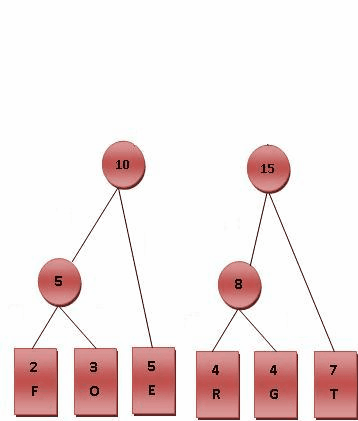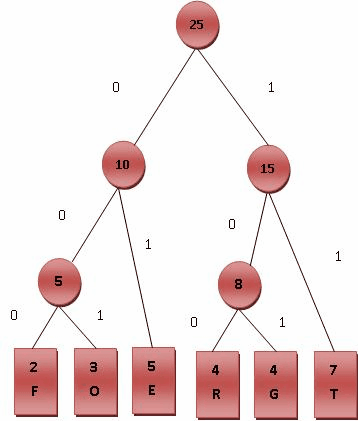
特点:只有度数为0和2的结点
C语言静态链表实现哈夫曼树
实现功能:输入一段英文文本,统计各字符出现次数作为权重,以当前字符集生成哈夫曼树,给出所有字符及指定编码与文本编码,再将编码后的文本解码为原文
数据结构定义
| 下标 | 数据域 | 父结点下标 | 左子树下标 | 右子树下标 |
|---|
typedef char ElementType;
typedef struct {
ElementTree data; 结点数据
int weight; 结点权重
int parent; 双亲下标
int left, right; 左右子树下标
}HuffmanTree;
- 统计字符及初始化静态链表
用下标从10 ~ 126的数组记录ASCII码10 ~ 126的字符,包含了英文文本的绝大多数字符
int num = 1;当前静态链表有效长度 [1,num)
char text[2005];//文本源
char *textAnalyze() {//返回字符集中字符个数的数组
char *chars = (char *)malloc(sizeof(char)*127);//32~126
char c = 0;
memset(chars, 0, sizeof(char)*127);
scanf("%[^
]", text);
int i = 0;
while (c = text[i++]) {
chars[c]++;//计数
}
for (i = 32; i <= 126; i++) {
if (chars[i]) {
printf("字符%c 出现%d次
", i, chars[i]);
}
}
return chars;
}
void initElement(HuffmanTree *nodes, char *chars) {
memset(nodes, 0, sizeof(char) * sizeof(HuffmanTree) * 200);
for (int i = 32; i <= 126; i++) {
if (chars[i]) {
nodes[num].data = i;
nodes[num].weight = chars[i];
nodes[num].parent = nodes[num].left = nodes[num].right = 0;
num++;//全局变量记录当前结点总数
}
}
free(chars);
}///////初始化静态链表完毕
eg:
输入为affgghhhjjj
此时静态链表为
| 下标 | 数据域 | 权重 | 父结点下标 | 左子树下标 | 右子树下标 |
|---|---|---|---|---|---|
| 1 | a | 1 | 0 | 0 | 0 |
| 2 | f | 2 | 0 | 0 | 0 |
| 3 | g | 2 | 0 | 0 | 0 |
| 4 | h | 3 | 0 | 0 | 0 |
| 5 | j | 3 | 0 | 0 | 0 |
建立哈夫曼树
void createHuffmanTree(HuffmanTree *nodes) {
每次连接两个结点,生成一个新结点,连接完成应该生成n-1个结点
故 n个结点建立的哈夫曼树应当有2n-1个结点
int end = num + num - 3;//计算总结点数
int *min = NULL;
while (num != end+1) {
min = searchOrder(nodes);
//制作新结点
nodes[num].weight = nodes[min[0]].weight + nodes[min[1]].weight;
nodes[num].left = min[0];
nodes[num].right = min[1];
//填补原结点
nodes[min[0]].parent = num;
nodes[min[1]].parent = num;
num++;
free(min);
}
}
其中searchOrder( )返回当前权重最小值与次小值的下标
int *searchOrder(HuffmanTree *nodes) {// num>=2
int *nums = (int *)malloc(sizeof(int) * 2);
int i = 1;
for (; i < num&&nodes[i].parent != 0; i++);//nodes[i].parent == 0 可用
1*- nums[0] = i;// 0 pre 1 later
for (i++; i < num&&nodes[i].parent != 0; i++);
nums[1] = i;//找到初始两下标
for (i++; i < num; i++) {
if (nodes[i].parent == 0) {//未使用
if (nodes[i].weight < nodes[nums[1]].weight) {// <min
nums[1] = i;
}
else if (nodes[i].weight < nodes[nums[0]].weight) {
nums[0]=nums[1],nums[1] = i;
}
}//按出现顺序生成最优二叉树
}
return nums;
}
此时的哈夫曼树为
| 下标 | 数据域 | 权重 | 父结点下标 | 左子树下标 | 右子树下标 |
|---|---|---|---|---|---|
| 1 | a | 1 | 6 | 0 | 0 |
| 2 | f | 2 | 6 | 0 | 0 |
| 3 | g | 2 | 7 | 0 | 0 |
| 4 | h | 3 | 7 | 0 | 0 |
| 5 | j | 3 | 8 | 0 | 0 |
| 6 | 3 | 8 | 1 | 2 | |
| 7 | 5 | 9 | 3 | 4 | |
| 8 | 6 | 9 | 5 | 6 | |
| 9 | 11 | 0 | 7 | 8 |
可以看出叶子结点左右孩子均为0,根结点父结点域为0
哈夫曼编码
前缀编码:每个字符的编码都不为其余编码的前缀
非前缀编码:存在某字符的编码是其余某编码的前缀
(没错就是这么扭曲)
所有参与编码的字符都在叶子结点上,因此保证编码为前缀编码
哈夫曼编码:走左子树为0,走右子树为1。从树根走到叶子结点组成的01序列
哈夫曼编码是前缀编码
- 遍历哈夫曼树得到每个叶子结点的编码
typedef struct {
ElementTree data;字符
char hfCode[115];该字符对应的编码序列
}HfCode;
HfCode codes[111];存储每个字符的哈夫曼编码
int charNum = 0;//字符集中的字符个数 [0,num)
char encodedText[4005];//编码后的文本
void encodeAll(HuffmanTree *nodes, int index, char *order, int cnt) {
if (nodes[index].left == nodes[index].right) {
printf("%c : ", nodes[index].data);
order[cnt] = 0;
puts(order);
codes[charNum].data = nodes[index].data;
strcpy(codes[charNum++].hfCode,order);
}
if (nodes[index].left) {
order[cnt] = '0';
encodeAll(nodes, nodes[index].left, order, cnt+1);
order[cnt] = '1';
encodeAll(nodes, nodes[index].right, order, cnt+1);
}
}
- 从叶子结点走到根得到该叶子的编码
void getCodeByChar(HuffmanTree *nodes, char leaf) {//得到某个叶子节点的编码
int index;
int end = num / 2;
for (index = 0; index <= end; index++) {
if (nodes[index].data == leaf)
break;
}
if (index > end) {
printf("输入有误!");
return;
}
char order[115];
int cnt = 0;
while (nodes[index].parent) {不为根
order[cnt++] = nodes[nodes[index].parent].left == index ? '0' : '1';
index = nodes[index].parent;
}
printf("%c : ", leaf);
for (cnt--; cnt >= 0; cnt--) {
printf("%c", order[cnt]);
}
printf("
");
}
在建立哈夫曼树并得到各字符编码的基础上对整个文本进行编码/解码就十分容易了
void encodeText(HuffmanTree *nodes) {//编码
int i, j, len = strlen(text);
printf("该信息为:
%s
", text);
printf("该信息的哈夫曼编码为:
");
for (i = 0; i < len; i++) {
for (j = 0; j < charNum&&codes[j].data != text[i]; j++);
strcat(encodedText, codes[j].hfCode);
}
printf("%s
",encodedText);
}
void decodeText(HuffmanTree *nodes, char *unknown) {//解码
int len = strlen(unknown);
int root = num - 1;
int i, index;
for (i = 0, index = root; i < len; i++) {
index = unknown[i] == '0' ? nodes[index].left : nodes[index].right;
if (nodes[index].left == 0) {
printf("%c", nodes[index].data);
index = root;
}
}
}
解码的主要思路是从哈夫曼树的根开始,遍历整个01序列,按照编码的方式,0向左走,1向右走,走到叶子结点输出,即译出一个字符,循环变量重新回到根结点继续解译下一个字符。因为前缀编码的前提保证,不会有歧义。
2019/11/19
编码的压缩存储
编码后的文件通常比原文件要大,因为每个字符以多个字符的01编码形式存储。既然是01编码,就有更为高效的存储方式。关键操作是将文本编码后得到的01串中的每个0或1以位的方式存储。
那么如何将01串的每个01按顺序填到 bit 上呢?
有两种解决方案:
- 利用位运算将编码后的01串按字节填到每一个 bit 上,再将得到的 char[ ] 写入文件
- 编码后的01串每八位一组,计算数值(char类型),再将得到的 char[ ] 写入文件
下面是位运算的方式将01串填成 char[ ]
将地址destination后第bits位为置0
void setZero(void *destination, int bits) {//将第bits位置0
char *des = (char *)destination;
char zero[8] = { 0b01111111,0b10111111,0b11011111,0b11101111,0b11110111,0b11111011,
0b11111101,0b11111110, };
int bit = bits / 8;//des前进字节数
bits = bits % 8;//目标位数
des += bit;
*des = *des&zero[bits];
}
将地址destination后第bits位为置1
void setOne(void *destinaton, int bits) {//将第bits为置1
char *des = (char *)destinaton;
char one[8] = { 0b10000000,0b01000000,0b00100000,0b00010000, 0b00001000,
0b00000100, 0b00000010, 0b00000001, };
int bit = bits / 8;//des前进字节数
bits = bits % 8;//目标位数
des += bit;
*des = *des|one[bits];
}
但是01串并不一定能刚好被8整除,因此多写入一个字节,表示最后一个字节的剩余量
比如说编码后的01串为
0000 1111 001(11位)
那么将写入 11/8+1=2 个字节 如果刚好16字节则不需要加1
再多写入一个数表示最后一个字节的补足位数 8-11%8=5 (需要补五位)
那么写入文件的两个表示数据的字节是
0x0F,0x20
表示余量的数是0x05
示例程序如下:
int main() {
char num[100]= {0};
char str[] = "000011110000100000100010";
int len = strlen(str);
for(int i = 0; i<len; i++) {
str[i]=='1'?setOne(num,i):setZero(num,i);
}
//写入
int left = 8-len%8;
int bits = len/8+(len/8?1:0);
FILE *fp = fopen("test.xx","wb");
fwrite(&left,1,1,fp);
int cnt = 0;
while(1){
fwrite(num+cnt,1,1,fp);
cnt++;
if(cnt==bits)break;
}
fclose(fp);
//读出
int get_left;
int get_bits = 0;//记录读取的字节数
char get_num[1000];//足够大小
fp = fopen("test.xx","rb");
fread(&get_left,1,1,fp);//读出补足字节数
while(fread(get_num+get_bits,1,1,fp)==1){
get_bits++;
}
fclose(fp);
//还原为01串
char get_str[100]={0};
cnt = 0;//为get_str赋值
char judge[] = { 0x80,0x40,0x20,0x10,0x08,0x04,0x02,0x01 };
for (int i = 0; i < get_bits-1; i++) {//先不读取最后一个有补足位数的byte
for (int bit = 0; bit < 8; bit++) {//取出每一位
get_str[cnt++] = ((get_num[i] & judge[bit]) == judge[bit]) ? '1' : '0';
}
}
for (int bit = 0; bit < 8-left; bit++) {//按补足位数读取最后一个字节
get_str[cnt++] = ((get_num[get_bits-1] & judge[bit]) == judge[bit]) ? '1' : '0';
}
// get_str[strlen(get_str)-left] = 0;//或使用left进行截断
puts(get_str);
return 0;
}
计算数值再写入文件的方法不再赘述。但注意可能遇到的大小端问题。
2019/6/21 更新
