关于“On the eigenvectors of $p$-Laplacian”目标函数的优化问题
作者:凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/
图p-拉普拉斯 (Graph p-Laplacian) / p-谱聚类算法 (p-spectral clustering) 从提出到现在有一些年景了,但关于目标函数的优化问题却很少被提及,而是直接引用前人[2]的结论。这篇博客,我们追根溯源,从最初提出图p-拉普拉斯开始,来探讨目标函数的优化(最小化)问题。
1. Graph $p$-Laplacian
给定一个带权无向图$G=(V, E)$,其中$V$是边集,$E$是点集。
$H(V)$: The Hilbert space of real-valued functions on each vertex.
$H(E)$: The Hilbert space of real-valued functions on each edge.
The graph $p$-Laplacian ${{Delta }_{p}}:H(V) o H(V)$ 为:
${{Delta }_{p}}f=-frac{1}{2}div({{left| abla f ight|}^{p-2}} abla f)$
其中$Delta $是拉普拉斯算子,$ abla $是梯度,$div$为散度。当$p=2$时,${{Delta }_{p}}f={{Delta }_{2}}f=-frac{1}{2}div( abla f)$,此时,图$p$-拉普拉斯退化为标准的图拉普拉斯。
通过引入函数$f$的二次型,标准图拉普拉斯算子${{Delta }_{2}}$满足:
$leftlangle f,{{Delta }_{2}}f ight angle =frac{1}{2}sumlimits_{i,jin V}{{{w}_{ij}}{{({{f}_{i}}-{{f}_{j}})}^{2}}}$
与图拉普拉斯类似,$p$-拉普拉斯算子[1]满足:
$leftlangle f,{{Delta }_{p}}f ight angle =frac{1}{2}sumlimits_{i,jin V}{{{w}_{ij}}{{left| {{f}_{i}}-{{f}_{j}} ight|}^{p}}}$
对于每一个节点$iin V$,未规范化的图$p$-拉普拉斯算子为:
${{(Delta _{p}^{w})}_{i}}=sumlimits_{jin V}{{{w}_{ij}}{{phi }_{p}}({{f}_{i}}-{{f}_{j}})},iin V$
其中${{phi }_{p}}(x)={{left| x ight|}^{p-1}}sig(x)$。
定义一个特征向量
${{(Delta _{p}^{w}f)}_{i}}={{lambda }_{p}}{{phi }_{p}}({{f}_{i}}),iin V$
注:特征向量在缩放时是不变的。
定理1:$f$是$p$-拉普拉斯的特征向量,当且仅当下列函数${{F}_{p}}$在$f$处有临界点:
${{F}_{p}}(f)=frac{leftlangle f,{{Delta }_{p}}f ight angle }{left| f ight|_{p}^{p}}=frac{sum olimits_{ij}{{{w}_{ij}}{{left| {{f}_{i}}-{{f}_{j}} ight|}^{p}}}}{2left| f ight|_{p}^{p}}$(广义Rayleigh-Ritz原理)
其中$left| f ight|_{p}^{p}=sum olimits_{i}{{{left| {{f}_{i}} ight|}^{p}}}, ext{ }i,jin V$,相应地特征值${{lambda }_{p}}$通过等式${{lambda }_{p}}={{F}_{p}}(f)$得出。
2. 用图$p$-拉普拉斯进行$K$聚类
Luo等人[2]通过求解下面的$p$-拉普拉斯嵌入问题,引入了对$p$-拉普拉斯全特征向量的一种近似,目标函数为:
$underset{F}{mathop{min }}\,{{J}_{E}}(F)=sumlimits_{k}{frac{sum olimits_{ij}{{{w}_{ij}}{{left| f_{i}^{k}-f_{j}^{k} ight|}^{p}}}}{left| {{f}^{k}} ight|_{p}^{p}}}$
$s.t. ext{ }{{F}^{T}}F=I.$
但是,在求导过程中出现错误,原文截图为:

也就是从这里起,后面的结果已经无效。
我推导的为:
$frac{partial {{J}_{E}}}{partial f_{i}^{k}}=frac{1}{left| {{f}^{k}} ight|_{p}^{p}}left[ psum olimits_{j}{{{w}_{ij}}{{phi }_{p}}(f_{i}^{k}-f_{j}^{k})}-psum olimits_{j}{{{w}_{ji}}{{phi }_{p}}(f_{j}^{k}-f_{i}^{k})} ight]-sum olimits_{ij}{{{w}_{ij}}{{left| f_{i}^{k}-f_{j}^{k} ight|}^{p}}}cdot frac{pcdot {{phi }_{p}}(f_{i}^{k})}{{{left( sum olimits_{i}{{{left| {{f}_{i}} ight|}^{p}}} ight)}^{2}}}$
$=frac{p}{left| {{f}^{k}} ight|_{p}^{p}}left[ 2sum olimits_{j}{{{w}_{ij}}{{phi }_{p}}(f_{i}^{k}-f_{j}^{k})}-frac{{{phi }_{p}}(f_{i}^{k})}{left| {{f}^{k}} ight|_{p}^{p}}sum olimits_{ij}{{{w}_{ij}}{{left| f_{i}^{k}-f_{j}^{k} ight|}^{p}}} ight]$
不管怎样,在求导的过程中,总会有系数$p$,而[2]中没有。可以认为这篇文章在求偏导的过程中出现问题。
算法总体流程:

注:(22)公式出错。
有趣的是,直接引用这篇文章结论的大有论文在。例如,这一篇[4]
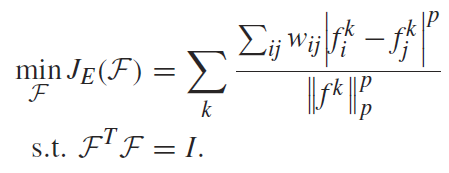

更有趣的是,时隔整整十年,[3]明确指出[2]中的推导错误:

[3]给出了他自己提的目标函数与求导公式:


可以看出,[3]的推导结论与我的推导是一致的,只是目标函数分母部分有无系数2。
3. 参考文献
[1] Bühler, Thomas & Hein, Matthias. (2009). Spectral clustering based on the graph Laplacian. Proceedings of the 26th International Conference On Machine Learning, ICML 2009. 382. 11-88. 10.1145/1553374.1553385. Code: p-Spectral Clustering
[2] Luo, Dijun & Huang, Heng & Ding, Chris & Nie, Feiping. (2010). On the eigenvectors of p-Laplacian. Machine Learning. 81. 37-51. 10.1007/s10994-010-5201-z.
[3] Pasadakis, Dimosthenis & Alappat, Christie & Schenk, Olaf & Wellein, Gerhard. (2020). $K$-way $p$-spectral clustering on Grassmann manifolds.
[4] W. Liu, X. Ma, Y. Zhou, D. Tao and J. Cheng, "$p$-Laplacian Regularization for Scene Recognition," in IEEE Transactions on Cybernetics, vol. 49, no. 8, pp. 2927-2940, Aug. 2019, doi: 10.1109/TCYB.2018.2833843.
[5] 拉普拉斯矩阵与拉普拉斯算子的关系 - 知乎
最后的思考:做研究切忌浮躁,要追根溯源,明白公式的来龙去脉,自己动手,丰衣足食。