珂朵莉树(ODT)笔记

珂朵莉树，又叫老司机树（$Old\, Driver \, Tree$）

是一种暴力出奇迹，就怕数据不随机的数据结构。

适用

需要用线段树维护一些区间修改的信息……

像是区间赋值（主要），区间加……

原理

暴力还需要原理吗……

首先通过维护区间及其中的值，使操作次数趋于$log N$

其次通过图省事高效的红黑树 set 维护区间保证$log N$的复杂度。

但是如果出题人毒瘤不讲情理卡珂朵莉树的话那也没办法。

最劣复杂度单次修改$Theta(N)$

区间太好看辣（雾

首先有区间$[1,Inf]$

突然我们想修改一段的值$[A,B]$为$1$

于是先把$[1,Inf]$切开，用三个不同的区间代替原区间。

那好了。

我们又后悔了，要把从$[C,D](C<A and B<D)$再赋$1$

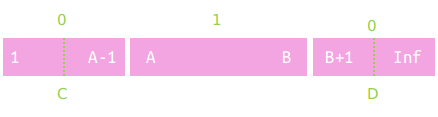
好多区间，怎么办？暴力

先切片。

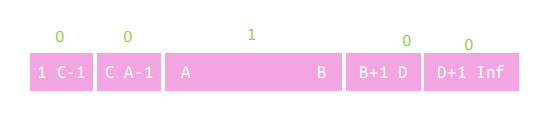
然后把过期的区间全部删掉！

最后补上一个修好的区间

实现

这里我们用 雅礼Day5-联 来稍讲

<内网链接>

首先要定义节点（就是区间）

struct Seg{
#define IT set<Seg> ::iterator
	LL l,r;
	mutable int v;
	Seg(LL l,LL r,int v){
		this->l=l;
		this->r=r;
		this->v=v;
	}
	friend bool operator < (const Seg &a,const Seg &b){
		return a.l<b.l;
	}
};

 里面有一点点内容。

 mutable 是 ’可变的‘ 关键字，在后面我们要在 set 上直接修值时必须把这个声明为可变

 下面重载$<$是为了把$Seg$塞进 set 里

一定要重定义一个$iterator$以后写函数要用。

然后是核心函数：$split$（切片）

IT split(LL pos){
	IT p=q.lower_bound(Seg(pos,0,-1));
	if(p!=q.end()&&p->l==pos)return p;
	p--;
	LL  l=p->l,
	    r=p->r;
	int v=p->v;
	q.erase(p);
	q.insert(Seg(l,pos-1,v));
	return q.insert(Seg(pos,r,v)).first;
}

这个函数的意义就是把$pos$所在的区间切开并返回后面一个区间的迭代器。

剩下所有的函数都以$split$为基础

区间修改：

void change(LL l,LL r,int v){
	IT rid=split(r+1),lid=split(l);
	q.erase(lid,rid);
	q.insert(Seg(l,r,v));
}

 区间异或$1$：

void filp(LL l,LL r){
	IT rid=split(r+1),lid=split(l);
	for(;lid!=rid;++lid) lid->v^=1;//在这里改
}

 如果想区间加或减就直接拿这个改

注意！一定要先切$r+1$再切$l$，不然，如果$l,r$位于一个区间，就会使$lid$维护的信息被$r+1$切开导致无效。

好像就没啥了，

现在是这个题的源码：

#include <iostream>
#include <cstring>
#include <cstdio>
#include <set>
#define N 111111
#define LL long long
using namespace std;

struct Seg{
#define IT set<Seg> ::iterator
	LL l,r;
	mutable int v;
	Seg(LL l,LL r,int v){
		this->l=l;
		this->r=r;
		this->v=v;
	}
	friend bool operator < (const Seg &a,const Seg &b){
		return a.l<b.l;
	}
};
set <Seg> q;
int qn;

IT split(LL pos){
	IT p=q.lower_bound(Seg(pos,0,-1));
	if(p!=q.end()&&p->l==pos)return p;
	p--;
	LL  l=p->l,
	    r=p->r;
	int v=p->v;
	q.erase(p);
	q.insert(Seg(l,pos-1,v));
	return q.insert(Seg(pos,r,v)).first;
}
void change(LL l,LL r,int v){
	IT rid=split(r+1),lid=split(l);
	//cout<<l<<" "<<r<<endl;
	//cout<<lid->l<<" "<<rid->l<<endl;
	q.erase(lid,rid);//puts("1");
	q.insert(Seg(l,r,v));
}
void filp(LL l,LL r){
	IT rid=split(r+1),lid=split(l);
	for(;lid!=rid;++lid) lid->v^=1;
}
LL query(){
	for(IT i=q.begin();i!=q.end();i++){
		if(i->v==0){
			return i->l;
		}
	}
	return (*--q.end()).r+1;
}
int main(){
	const LL MAXN=100000000000000001;
	LL l,r;
	int opt;
	scanf("%d",&qn);
	q.insert(Seg(1,MAXN,0));
	for(int i=1;i<=qn;i++){
		scanf("%d%lld%lld",&opt,&l,&r);
		if(l>r)continue;
		switch(opt){
			case 1://puts("61");
				change(l,r,1);//puts("10");
				break;
			case 2:
				change(l,r,0);
				break;
			case 3:
				filp(l,r);
				break;
		}//puts("21");
		printf("%lld
",query());
	}
}