核方法(Kernel Methods)
支持向量机(SVM)是机器学习中一个常见的算法,通过最大间隔的思想去求解一个优化问题,得到一个分类超平面。对于非线性问题,则是通过引入核函数,对特征进行映射(通常映射后的维度会更高),在映射之后的特征空间中,样本点就变得线性可分了。
核方法的示意图如下:
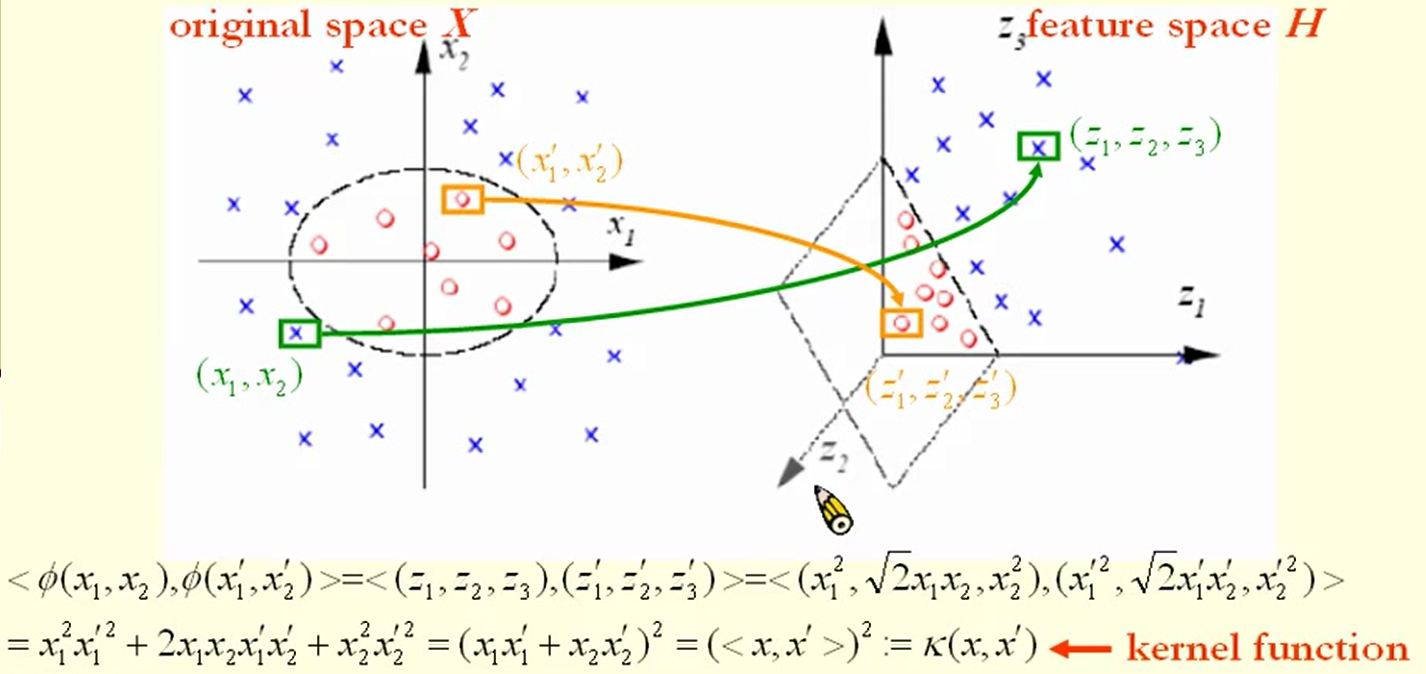
上图中左边表示的是原始特征空间,在原始特征空间中,我们无法用直线(平面)来将两类点分开,但是却可以用圆来进行分割。右边表示的通过对原始样本点进行映射(从二维映射到三维)得到的新的样本点。可以看到在新的特征空间中,两类样本点可以通过一个平面分开。
核方法的应用除了在支持向量机之外,在感知机上,对应<xi,xj>的位置利用核函数代替,就有了核感知机;同理还有核聚类,核PCA等。
常用的核函数

除了上述的核函数之外,还有Sigmoid核函数,并且将核函数进行线下组合,也仍然是核函数。
核函数定义
知道了核函数的应用以及有哪些核函数之后,我们来看看,什么样的函数能作为核函数,是不是我们能自己构造核函数。
核函数一个有效的判断方式是通过Mercer定理:

简单的说就是,判断核函数K对应的Gram矩阵是否是半正定的。但是值得注意的是,Mercer定理不是核函数必要条件,只是一个充分条件,也就是说还有不满足Mercer定理的函数也可以是核函数。
参考:

