有关1~n的m次方和的快速计算；

首先，我们可以知道，这个$sum_{i=1}^{n}i^{m}$的通项公式是一个m+1次的多项式;

下面就对其正确性进行论证；

我们设多项式：$f(x)=sum_{i=0}^{n}u_{i}x^{i}$

设对于数列a{ },a[x]=f(x);

假如b{x}=a[x+1]-a[x]; 那么显然：$b[x]=sum_{i=0}^{n}u_{i}(x+1)^{i}-sum_{i=0}^{n}u_{i}x^{i}$

对于上面的式子，加入我们只考虑$x^{v}$,显然只有i=v的时候才又可能出现$x^{v}这一项$

那么式子可以看成：$b[x]=u_{v}(x+1)^{v}-u_{v}x^{v}$

由于我们只考虑$x^{v}$,所以$(x+1)^{v}$完全可以看成$x^{v}$

式子可以简化为：$b[x]=u_{v}x^{v}-u_{v}x^{v}=0$

发现了没有发现了没有？对于一个可以用n次多项式表示通项公式的数列a，它的差分数列b中的通项公式不会出现x的n次幂，也就是说，b的通项公式是一个(n-1)次多项式！

也就是说，做一次差分之后数列的通项公式的多项式次数会-1；

对于$sum_{i=1}^{n}i^{m}$,原数列a{ }是：

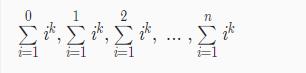
那么它的差分数列b{ }就是：

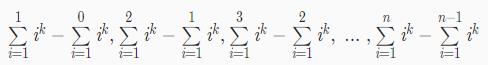
即：$b[x]=x^{k}$

嘿！b[x]这可是一个k次多项式啊！那么根据之前所推，a[x]不就是一个(k+1)次多项式吗？

所以说,$sum_{i=1}^{n}x^{m}$的通项公式是一个(m+1)次的多项式；

好了~完结撒花~；

接下来的步骤就很套路了，根据拉格朗日插值的特点，我们选取任意连续的值xi，求出他们所对应的多项式的值yi,然后利用插值法O(n)的计算f(n)就好了；

具体的求法见我的这篇博客：(传送门)

#include <bits/stdc++.h>
#define p 1000000007
#define inc(i,a,b) for(register int i=a;i<=b;i++)
#define dec(i,a,b) for(register int i=a;i>=b;i--)
using namespace std;
long long x[1000010],y[1000010];
long long KSM(long long a,long long b){
    long long res=1;
    while(b){
        if(b&1) res=res*a%p;
        a=a*a%p;
        b/=2;
    }
    return res%p;
}
long long pre[1000010],suf[1000010],fac[1000010];
int main()
{
    long long n,m;
    cin>>n>>m;
    long long sum=0;
    inc(i,1,m+1){
        long long tmp=KSM(i,m);
        sum=(sum+tmp)%p;
        x[i]=i; y[i]=sum;
    }
    long long ans=0;
    pre[0]=n; fac[0]=1;
    inc(i,1,m+1) pre[i]=pre[i-1]*(n-i)%p,fac[i]=fac[i-1]*i%p;
    suf[m+1]=((n-x[m+1])%p+p)%p;
    dec(i,m,0) suf[i]=suf[i+1]*(n-i)%p;
    inc(i,0,m+1){
        long long tmp1=pre[i-1];
        long long tmp2=suf[i+1]; 
        if(i==0) tmp1=1;
        if(i==m+1) tmp2=1;
        long long tmp3=y[i]*tmp1%p*tmp2%p;
        if((m+1-i)%2==0) ans=(ans+tmp3*KSM((fac[i]*fac[m+1-i]%p),p-2)%p);
        else ans=(ans+tmp3*KSM((((-fac[i]*fac[m+1-i])%p+p)%p),p-2)%p);
    }
    
    /*    
    inc(i,0,m+1){
        long long tmp=1;
        inc(j,0,m+1){
            if(i==j) continue;
            tmp=(tmp*(n-j)%p*KSM(i-j,p-2)%p);
        }
        ans=(ans+y[i]*tmp%p)%p;
    }
    */
    cout<<(ans%p+p)%p;
}

然后可以水掉这一道题 ：[TJOI2018]教科书般的亵渎

小豆喜欢玩游戏，现在他在玩一个游戏遇到这样的场面,每个怪的血量为$a^i$，且每个怪物血量均不相同，小豆手里有无限张“亵渎”。亵渎的效果是对所有的怪造成$1$点伤害，如果有怪死亡，则再次施放该法术。我们认为血量为$0$怪物死亡。

小豆使用一张 “亵渎”会获得一定的分数，分数计算如下，在使用一张“亵渎”之后，每一个被亵渎造成伤害的怪会产生$x^k$,其中$x$是造成伤害前怪的血量为$x$和需要杀死所有怪物所需的“亵渎”的张数$k$。

输入格式

第一行输入一个$T$($T\le 10$)，表示有多少组测试数据

每组组测试数据第一行为$n$，$m$，表示有当前怪物最高的血量$n$，和$m$种没有出现的血量

接下来$m$行，每行$1$个数$a^i$，表示场上没有血量为$a^i$的怪物

输出格式

一共$T$行，每行一个数， 第$i$行表示第$i$组测试数据中小豆的最后可以获得的分数, 因为这个分数会很大需要模$10^9+7$

#include <bits/stdc++.h>
#define p 1000000007
#define inc(i,a,b) for(register int i=a;i<=b;i++)
#define dec(i,a,b) for(register int i=a;i>=b;i--)
using namespace std;
long long x[1000010],y[1000010];
long long KSM(long long a,long long b){
    long long res=1;
    while(b){
        if(b&1) res=res*a%p;
        a=a*a%p;
        b/=2;
    }
    return res%p;
}
long long pre[1000010],suf[1000010],fac[1000010];
int solve(long long n,long long m)
{
    long long sum=0;
    inc(i,1,m+1){
        long long tmp=KSM(i,m);
        sum=(sum+tmp)%p;
        x[i]=i; y[i]=sum;
    }
    pre[0]=n; fac[0]=1;
    inc(i,1,m+1) pre[i]=pre[i-1]*(n-i)%p,fac[i]=fac[i-1]*i%p;
    suf[m+1]=((n-x[m+1])%p+p)%p;
    dec(i,m,0) suf[i]=suf[i+1]*(n-i)%p;
    long long ans=0;
    inc(i,0,m+1){
        long long tmp1=pre[i-1];
        long long tmp2=suf[i+1]; 
        if(i==0) tmp1=1;
        if(i==m+1) tmp2=1;
        long long tmp3=y[i]*tmp1%p*tmp2%p;
        if((m+1-i)%2==0) ans=(ans+tmp3*KSM((fac[i]*fac[m+1-i]%p),p-2)%p);
        else ans=(ans+tmp3*KSM((((-fac[i]*fac[m+1-i])%p+p)%p),p-2)%p);
    }
    return ((ans%p)+p)%p;
}
long long a[100];
int main()
{    
    int T;
    cin>>T;
    while(T--){
        long long ans=0;
        long long tot;
        int num; scanf("%lld%d",&tot,&num);
        inc(i,1,num) scanf("%lld",&a[i]);
        sort(a+1,a+1+num);
        while(a[num]==tot){
            --num;
            --tot;
        }
        long long k=num+1;
        int now=1;
        while(now<=k){
            ans=(ans+solve(tot,k))%p;
            inc(i,now,num){
                ans=((ans-KSM(a[i],k))+p)%p;
            }
            tot=(tot-a[now]);
            long long tmp=a[now];
            inc(i,now,num){
                a[i]-=tmp;
            }
            ++now;
        }
        printf("%lld
",ans);
    }
}
/*
2
4 2
1
2
10 1
5

*/

[TJOI2018]教科书般的亵渎