

费用流比较显然,但复杂度并不是我们想要的那样。这时候考虑模拟费用流是个不错的选择。
我们把缺军队的地方看作老鼠,军队为洞,那么我们可以花费一定代价移动老鼠和洞,使得所有老鼠均进洞,我们需要最小化总代价。
为了方便,我们将每个老鼠的值设为$-inf$。表示将该老鼠和某一个洞匹配后额外的代价。由于我们会最小化总代价,因此这样将保证所有老鼠均进洞。
这样算到最后,我们只需要把答案加上$老鼠的个数 imes inf$就好了。
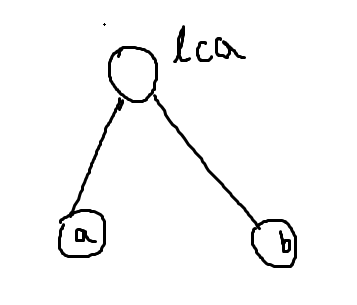
我们看这副图。假如我们知道a是老鼠b是洞,那么贡献显然是$dep[a]+dep[b]-2*dep[lca]$。
但是这并不代表答案就是它了。因为可能以后会反悔。
这时候一个性质会被我们需要:一个点最多反悔1次,也就是说要么就是老鼠反悔要么就是洞反悔。
看图就很容易明白:不交叉永远比交叉好。
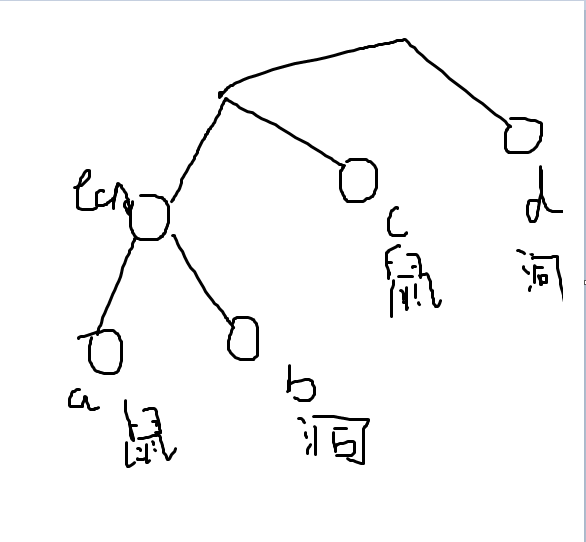
我们考虑假如洞b变成了洞d,那么:

答案变成了什么呢?我们考虑原来的答案是:$dep[a]+dep[b]-2dep[lca]$,而现在的变成了$dep[a]+dep[d]-2dep[g]$。
这其中改变了什么呢?我们可以这么看:如果将a的权值改成$-dep[b]+2dep[lca]$,再次选择a(相当于之后反悔a了)就相当于将原来的答案$-dep[b]+2dep[lca]$变成了$dep[a]$,然后和洞d合并变成$dep[a]+dep[d]-2dep[g]$。
对于洞也和老鼠一样进行类似的反悔操作。这样就可以完成模拟费用流啦。(当dep[a]+dep[b]-2dep[lca]<0的时候允许进行反悔)
#include <bits/stdc++.h> #include<ext/pb_ds/priority_queue.hpp> #define int long long #define inc(i,a,b) for(register int i=a;i<=b;i++) using namespace std; int n,head[300010],cnt,m; class littlestar{ public: int to,nxt,w; void add(int u,int v,int ww){ to=v; nxt=head[u]; head[u]=cnt; w=ww; } }star[600010]; long long ans,dep[600010],inf=1e12; int army[300010],goal[300010]; __gnu_pbds::priority_queue<long long,greater<long long> >q1[300010],q2[300010]; void dfs(int u,int fa){ while(army[u]--) q1[u].push(dep[u]); while(goal[u]--) q2[u].push(dep[u]-inf); for(int i=head[u];i;i=star[i].nxt){ int v=star[i].to; if(v==fa) continue; dep[v]=dep[u]+star[i].w; dfs(v,u); q1[u].join(q1[v]); q2[u].join(q2[v]); } while(q2[u].size()&&q1[u].size()&&q2[u].top()+q1[u].top()-2*dep[u]<0){ long long tmp1=q2[u].top(),tmp2=q1[u].top(),summ=tmp1+tmp2-2*dep[u]; ans+=summ; q2[u].pop(), q1[u].pop(); q2[u].push(tmp1-summ); q1[u].push(tmp2-summ); } } signed main(){ cin>>n; inc(i,1,n-1){ int x,y,z; scanf("%lld%lld%lld",&x,&y,&z); star[++cnt].add(x,y,z); star[++cnt].add(y,x,z); } inc(i,1,n){ scanf("%lld%lld",&army[i],&goal[i]); int tmp=min(army[i],goal[i]); army[i]-=tmp; goal[i]-=tmp; m+=goal[i]; } dfs(1,0); cout<<ans+inf*m; }