题目描述
在有向图 G 中,每条边的长度均为 1,现给定起点和终点,请你在图中找一条从起点到终点的路径,该路径满足以下条件:
- 路径上的所有点的出边所指向的点都直接或间接与终点连通。
- 在满足条件1的情况下使路径最短。
注意:图 G中可能存在重边和自环,题目保证终点没有出边。
请你输出符合条件的路径的长度。
输入格式
第一行有两个用一个空格隔开的整数 n 和 m,表示图有 n 个点和 m 条边。
接下来的 m行每行 2 个整数 x,y,之间用一个空格隔开,表示有一条边从点 x 指向点y。
最后一行有两个用一个空格隔开的整数 s, t,表示起点为 s,终点为 t。
输出格式
输出只有一行,包含一个整数,表示满足题目描述的最短路径的长度。如果这样的路径不存在,输出-1。
输入输出样例
输入 #1
3 2 1 2 2 1 1 3
输出 #1
-1
输入 #2
6 6 1 2 1 3 2 6 2 5 4 5 3 4 1 5
输出 #2
3
说明/提示
解释1:
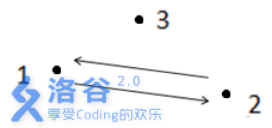
如上图所示,箭头表示有向道路,圆点表示城市。起点11与终点33不连通,所以满足题目描述的路径不存在,故输出-1−1 。
解释2:
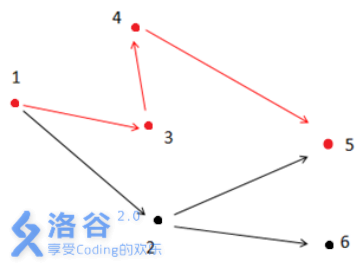
如上图所示,满足条件的路径为1- >3- >4- >5。注意点2 不能在答案路径中,因为点2连了一条边到点6,而点6 不与终点5连通。
【数据范围】
对于30%的数据,0<n≤10,0<m≤20;
对于60%的数据,0<n≤100,0<m≤2000;
对于100%的数据,0<n≤10000,0<m≤200000,0<x,y,s,t≤n,x,s≠t。
分析:
本题较为复杂,对于条件2,不难想到求最短路即可,但是条件1的话,我们可以通过反向加边来处理即可,然后记住标记一下。
不过话说为什么dfs会炸???
解答:本人自己认为是由于dfs深度问题emmm
dfs得分:

所以尽量用bfs!!!血的教训QAQ
CODE:
1 #include<cmath> 2 #include<cstdio> 3 #include<cstring> 4 #include<iostream> 5 #include<algorithm> 6 #include<queue> 7 using namespace std; 8 const int M=400005; 9 const int inf=1<<20; 10 int n,m; 11 int s,t; 12 int tot,head[M],to[M],next[M]; 13 bool flag[M]; 14 int f[M],e[M]; 15 int get(){ 16 int res=0,f=1; 17 char c=getchar(); 18 while (c>'9'||c<'0') { 19 if (c=='-') f=-1; 20 c=getchar(); 21 } 22 while (c<='9'&&c>='0'){ 23 res=(res<<3)+(res<<1)+c-'0'; 24 c=getchar(); 25 } 26 return res*f; 27 } 28 void add(int u,int v){ 29 next[++tot]=head[u]; 30 head[u]=tot; 31 to[tot]=v; 32 return ; 33 } 34 queue<int> Q; 35 void bfs(){ 36 Q.push(t); 37 flag[t]=true; 38 while (!Q.empty()){ 39 int u=Q.front(); 40 Q.pop(); 41 for (int i=head[u];i;i=next[i]){ 42 if (!flag[to[i]]) { 43 Q.push(to[i]); 44 flag[to[i]]=true; 45 } 46 } 47 } 48 return ; 49 } 50 bool flagg[M]; 51 void dfs(int u){ 52 for (int i=head[u];i;i=next[i]){ 53 int v=to[i]; 54 flagg[v]=false; 55 } 56 } 57 int dis[M]; 58 bool bj[M]; 59 queue<int> q; 60 void spfa(){ 61 for (int i=1;i<=n;i++) dis[i]=inf; 62 dis[s]=0; 63 bj[s]=true; 64 q.push(s); 65 while (!q.empty()){ 66 int u=q.front(); 67 q.pop(); 68 bj[u]=false; 69 for (int i=head[u];i;i=next[i]){ 70 int v=to[i]; 71 if (dis[u]+1<dis[v]) { 72 dis[v]=dis[u]+1; 73 if (!bj[v]){ 74 bj[v]=true; 75 q.push(v); 76 } 77 } 78 } 79 } 80 return ; 81 } 82 int main(){ 83 n=get(),m=get(); 84 for (int i=1;i<=m;i++){ 85 f[i]=get(),e[i]=get(); 86 add(e[i],f[i]); 87 } 88 s=get(),t=get(); 89 bfs(); 90 for (int i=1;i<=n;i++) flagg[i]=true; 91 for (int i=1;i<=n;i++) 92 if (!flag[i]) dfs(i); 93 tot=0; 94 memset(head,0,sizeof(head)); 95 memset(next,0,sizeof(next)); 96 //for (int i=1;i<=n;i++) cout<<flag[i]<<endl; 97 //for (int i=1;i<=n;i++) cout<<flagg[i]<<endl; 98 for (int i=1;i<=m;i++) 99 if (flag[f[i]]&&flag[e[i]]&&flagg[f[i]]&&flagg[e[i]]) add(f[i],e[i]); 100 spfa(); 101 if (dis[t]==inf) printf ("-1 "); 102 else printf ("%d ",dis[t]); 103 return 0; 104 }