二分法小结

二分法是一个神奇的东西，弄了半天，总算知道怎样合理的去使用了

常规的二分法正确的时候返回正确的下标或值，在找不到的情况下，返回比要查找的数稍大点的数(已排序），

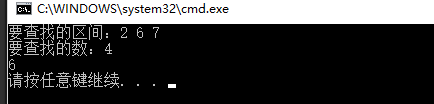
#include<iostream>
using namespace std;

int main()
{
    int b = 4, a[] = { 2,6,7 };
    int i = 0, j = 2;
    while (i < j)
    {
        int mid = i + (j - i) / 2;
        if (a[mid] >= b) j = mid;
        else i = mid+1;
    }
    cout << "要查找的区间：" << "2 6 7 " << endl;
    cout << "要查找的数：4" << endl;
    cout << a[i] << endl;
}

而另外的一种二分，可使返回正确的值，若无，则返回尽量小的数

#include<iostream>
using namespace std;

int main()
{
    int b = 4, a[] = { 2,6,7 };
    int i = 0, j = 2;
    while (i < j-1)
    {
        int mid = i + (j - i) / 2;
        if (a[mid] > b) j = mid;
        else i = mid;
    }
    cout << "要查找的区间：" << "2 6 7 " << endl;
    cout << "要查找的数：4" << endl;
    cout << a[i] << endl;
}

（两种方法的不同之处在于跳出循环的条件不同）