C++实现矩阵类和向量类

C++期末作业内容，写完之后觉得过于臃肿，又重新搞了个新的。新的当作业交，旧的拿来给同学参考。

【问题描述】请仿照复数类，设计一个矩阵类，设计矩阵类的构成元素
1.编写构造函数完成初始化
2.编写成员函数，读入一个矩阵，输出一个矩阵
3.编写成员函数，计算两个矩阵相加、相减、点乘
4.编写成员函数，利用运算符重载计算两个矩阵的相加、相乘、点乘、输出，并输出计算结果
例如输入3 3，表示是一个3*3的矩阵，输入一个矩阵
1.0 1.0 1.0
3.0 3.0 3.0
6.0 6.0 6.0
再输入3 3，再输入一个矩阵
9.0 9.0 9.0
6.0 6.0 6.0
5.0 5.0 5.0
输出相加的结果为
10.0 10.0 10.0
9.0 9.0 9.0
11.0 11.0 11.0
输出相减的结果为
-8.0 -8.0 -8.0
-3.0 -3.0 -3.0
1.0 1.0 1.0
输出点乘的结果为
20.0 20.0 20.0
60.0 60.0 60.0
120.0 120.0 120.0

【问题描述】基于以上的矩阵类和向量类，编写友元函数计算矩阵乘以向量
例如
例如输入3 3，表示是一个3*3的矩阵，输入一个矩阵
1.0 1.0 1.0
3.0 3.0 3.0
6.0 6.0 6.0
例如输入3，表示是一个3维列向量，输入一个列向量
1.2 3.4 5.6
输出结果为
10.2 30.6 61.2

#include <iostream>
using namespace std;
const int MAXDIMENSION=100; //维数上限 
class Vector{ //向量类 
	private:
		double value[MAXDIMENSION]; //向量的值 
		int dimension; //向量的维数 
	public:
		Vector(){}
		Vector(Vector& source){
			dimension=source.getDimension();
			for(int i=0;i<dimension;i++){
				value[i]=source.getValue(i);
			}
		}
		void setValue(int i,double newvalue){
			value[i]=newvalue;
		}
		double getValue(int i){
			return value[i];
		}
		void setDimension(int newDimension){
			dimension=newDimension;
		}
		int getDimension(){
			return dimension;
		}
		void input(){
			cin>>dimension;
			for(int i=0;i<dimension;i++){
				cin>>value[i];
			}
		}
		void output(){
			for(int i=0;i<dimension;i++){
				cout<<value[i]<<' ';
			}
			cout<<'
';
		}
		Vector operator +(Vector& right){
			Vector left(*this);
			for(int i=0;i<dimension;i++){
				left.setValue(i,left.getValue(i)+right.getValue(i));
			}
			return left;
		}
		Vector operator -(Vector& right){
			Vector left(*this);
			for(int i=0;i<dimension;i++){
				left.setValue(i,left.getValue(i)-right.getValue(i));
			}
			return left;
		}
		double operator *(Vector& right){ //向量相乘，结果为一个数，而不是向量
			Vector left(*this);
			double ans=0;
			for(int i=0;i<dimension;i++){
				ans+=left.getValue(i)*right.getValue(i);
			}
			return ans;
		}
};
class Matrix{ //矩阵类 
	private:
		double value[MAXDIMENSION][MAXDIMENSION]; //矩阵的值 
		int row,column; //行数  列数 
	public:
		Matrix(){}
		Matrix(Matrix& source){
			row=source.getRow();
			column=source.getColumn();
			for(int i=0;i<row;i++){
				for(int j=0;j<column;j++){
					value[i][j]=source.getValue(i,j);
				}
			}
		}
		void setValue(int r,int c,double newvalue){
			value[r][c]=newvalue;
		}
		double getValue(int r,int c){
			return value[r][c];
		}
		void setRow(int newRow){
			row=newRow;
		}
		int getRow(){
			return row;
		}
		void setColumn(int newColumn){
			column=newColumn;
		}
		int getColumn(){
			return column;
		}
		void input(){
			cin>>row>>column;
			for(int i=0;i<row;i++){
				for(int j=0;j<column;j++){
					cin>>value[i][j];
				}
			}
		}
		void output(){
			for(int i=0;i<row;i++){
				for(int j=0;j<column;j++){
					cout<<value[i][j]<<' ';
				}
				cout<<'
';
			}
		}
		Matrix operator +(Matrix& right){
			Matrix left(*this);
			for(int i=0;i<row;i++){
				for(int j=0;j<column;j++){
					left.setValue(i,j,left.getValue(i,j)+right.getValue(i,j));
				}
			}
			return left;
		}
		Matrix operator -(Matrix& right){
			Matrix left(*this);
			for(int i=0;i<row;i++){
				for(int j=0;j<column;j++){
					left.setValue(i,j,left.getValue(i,j)-right.getValue(i,j));
				}
			}
			return left;
		}
		Matrix operator *(Matrix& right){
			Matrix result;
			result.setRow(getRow());
			result.setColumn(right.getColumn());
			for(int i=0;i<result.getRow();i++){
				for(int j=0;j<result.getColumn();j++){
					for(int k=0;k<this->getColumn();k++){
						result.setValue(i,j,result.getValue(i,j)+this->getValue(i,k)*right.getValue(k,j));
					}
				}
			}
			return result;
		}
		Matrix mulVector(Vector vec){ //矩阵乘向量，我觉得并不需要用到友元函数 
			Matrix result;
			result.setColumn(vec.getDimension());
			result.setRow(1);
			for(int i=0;i<this->getRow();i++){
				for(int j=0;j<this->getColumn();j++){
					result.setValue(0,i,result.getValue(0,i)+this->getValue(i,j)*vec.getValue(j));
				}
			}
			return result;
		}
};

int main(){
	Vector a,b,c;
	Matrix d,e,f;
	cout<<"请输入向量维数和值:
";
	a.input();
	cout<<"请输入向量维数和值:
";
	b.input();
	cout<<"向量相加为:
";
	c=a+b;
	c.output();
	cout<<"向量相减为:
";
	c=a-b;
	c.output();
	cout<<"向量相乘为:
";
	cout<<a*b<<"
";
	cout<<"请输入矩阵的行数列数和值:
";
	d.input();
	cout<<"请输入矩阵的行数列数和值:
";
	e.input();
	cout<<"矩阵相加为:
";
	f=d+e;
	f.output();
	cout<<"矩阵相减为:
";
	f=d-e;
	f.output();
	cout<<"矩阵相乘为:
";
	f=d*e;
	f.output();
	cout<<"请输入矩阵的行数列数和值:
";
	e.input();
	cout<<"请输入向量的维数和值:
";
	a.input();
	cout<<"矩阵乘向量结果为:
";
	f=e.mulVector(a);
	f.output();
	return 0;
}

测试数据:

3
1.2 3.4 5.6
3
7.8 9.0 2.1
3 3
1.0 1.0 1.0
3.0 3.0 3.0
6.0 6.0 6.0
3 3
9.0 9.0 9.0
6.0 6.0 6.0
5.0 5.0 5.0
3 3
1.0 1.0 1.0
3.0 3.0 3.0
6.0 6.0 6.0
3
1.2 3.4 5.6

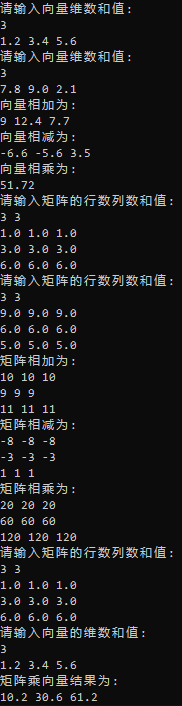
测试结果：

原写于2019年05月28日 12:37:45