算法竞赛模板 根据遍历序列确定二叉树

转自：https://blog.csdn.net/sinat_39253550/article/details/73614755

已知二叉树的先序序列和中序序列

1.在先序序列中，第一个结点一定是二叉树的根结点。
2.在中序序列中，根结点必然将中序序列分割成两个子序列；前一个子序列是根结点的左子树的中序序列，后一个是右子树的的中序序列。
3.根据这两个子序列，在先序序列中找到对应的左右子序列。
4.在先序序列中，左子序列的第一个结点是左子树的根结点，右子序列同理。 
5.如此递归下去……

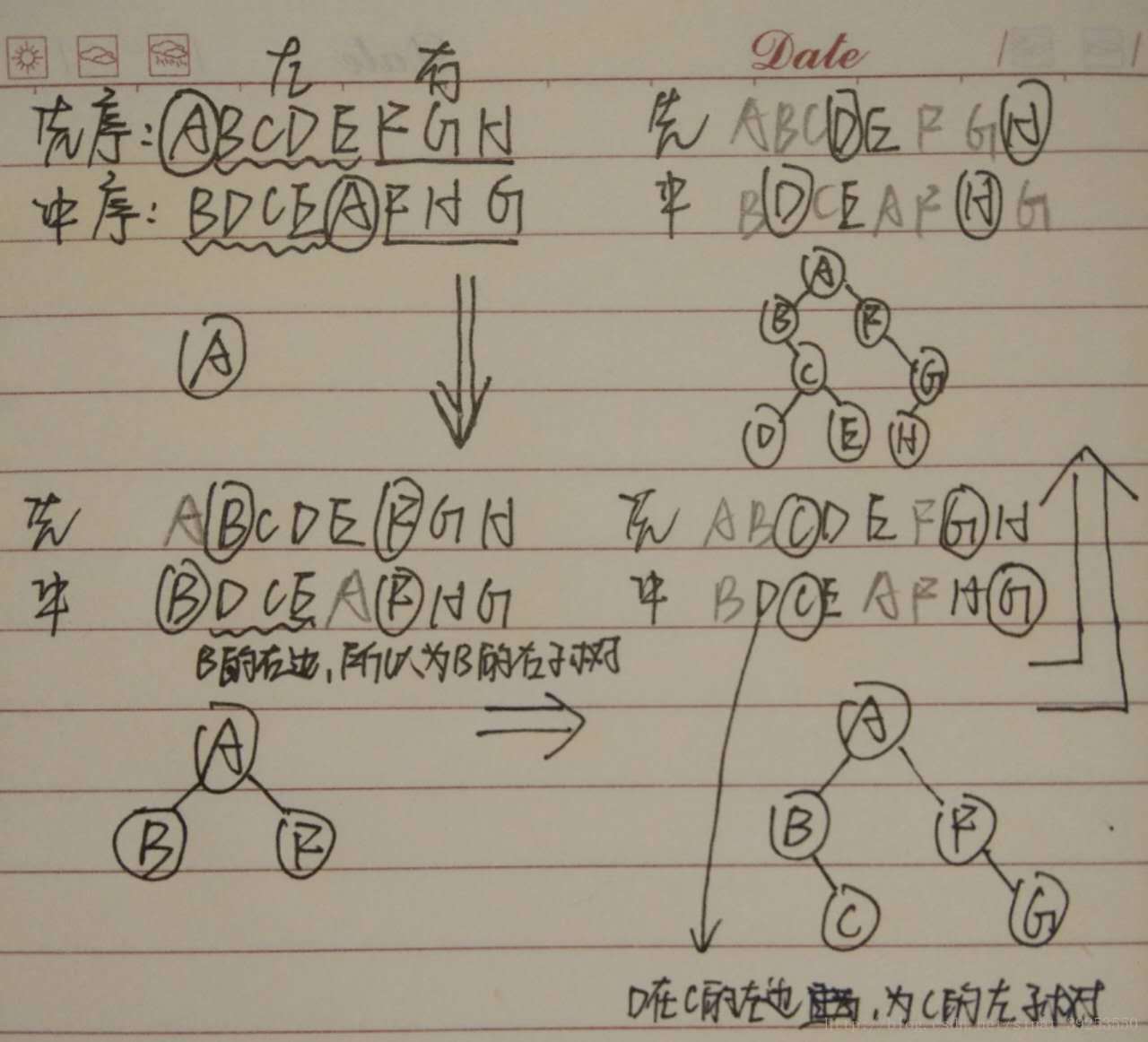
总结：

先序配合中序时，中序负责找左右子序列，先序负责找子树的根节点。

已知二叉树的中序序列和后序序列

1.在后序序列，最后一个结点一定是二叉树的根结点。
2.在中序序列中，根结点必然将中序序列分割成两个子序列；前一个子序列是根结点的左子树的中序序列，后一个是右子树的的中序序列。
3.根据这两个子序列，在后序序列中找到对应的左右序列。
4.在后序序列中，左子序列的最后一个结点是左子树的根结点，右子序列同理 。
5.如此递归下去……

总结：

后序配合中序时，中序负责找左右子序列，后序负责找子树的根结点。

注意：根据先序序列和后序序列是不能确定一个二叉树的

#include<bits/stdc++.h>
using namespace std;
int n,post[35],in[35],res[10005];
//root-根结点在后序序列中的下标，s、e-中序子序列的首尾，index-数组存二叉树的下标
void build(int root,int s,int e,int index)
{
    if(s>e)return;
    int i;
    for(i=s;i<e&&in[i]!=post[root];i++);//找根结点在中序序列中的位置

    res[index]=post[root];              //找到就存起来
    //通过中序序列判断左右子树
    //e-i为右子树结点数量，所以root-(e-i)-1即为左子树的根结点
    build(root-1-e+i,s,i-1,index*2+1);  //建立左子树
    build(root-1,i+1,e,index*2+2);        //建立右子树
}
int main()
{
    cin>>n;
    int i;
    for(i=1;i<=n;i++)
        cin>>post[i];
    for(i=1;i<=n;i++)
        cin>>in[i];
    build(n,1,n,1);
    int cnt=0;
    for(i=1;cnt<n;i++)
    {
        if(res[i])
        {
            cnt++;
            if(cnt<n)cout<<res[i]<<" ";
            else cout<<res[i]<<endl;
        }
    }
    return 0;
}

综上所述：

配合中序序列时，先序和后序都是确定子树的根结点，区别是根结点在其子序列的位置（先序是子序列的第一个，后序是子序列的最后一个）；而中序序列都是在先序或后序序列找到根结点后，找到左右子序列。