算法竞赛模板 折线分割平面

①求n条“V”型折线所能分割的最大平面数：

(1) 当增加第n条直线时，为了使平面最多，则第n条直线要与前面2*(n-1)条直线都相交，且没有任何三条直线相交于一点。

(2) 作图可知，每作出一条符合条件的直线，就会有[2*(n-1)+1]个新平面生成，所以两条平行直线就会新生成2*[2*(n-1)+1]个平面。

(3) 但由于是通过折线分割，所以两条平行直线会交于一点，在新生成的平面中会有2个平面合成1个平面，则第n条折线新增加的平面数为2*[2*(n-1)+1]-1=4*n-3；

图示：

#include<bits/stdc++.h>
#define MAX 10005
using namespace std;
int main()
{
    int a[MAX],n,i;
    a[1]=2;
    for(i=2;i<=MAX;i++)
        a[i]=a[i-1]+4*i-3;
    while(cin>>n)
        cout<<a[n]<<endl;
    return 0;
}

②求n条“Z”型折线所能分割的最大平面数：

(1) 当增加第n条直线时，为了使平面最多，则第n条直线要与前面3*(n-1)条直线都相交，且没有任何三条直线相交于一点。

(2) 作图可知，每作出一条符合条件的直线，就会有[3*(n-1)+1]个新平面生成，所以三条平行直线就会新生成3*[3*(n-1)+1]个平面。

(3) 又由于是“Z”型折线，共出现了2次折线，每一个折线都会使2个平面合成1个平面，所以在原来的基础上要-2，则第n条直线新增加的平面数为3*[3*(n-1)+1]-2=9*n-8；

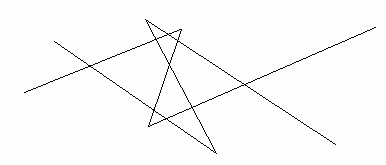
图示：

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int i,n,a[10001];
    a[1]=2;
    for(i=2;i<=10000;i++)
        a[i]=a[i-1]+9*i-8;
        
    while(cin>>n)
    {
        printf("%d
",a[n]);
    }
    return 0;
}