简介:
《算法设计手册》(The Algorithm Design Manual)课后面试题和解答。包括:未知大小的集合选取k个元素、数据备份方案、寻找数组最小数时赋值语句执行次数的期望、100层大楼抛大理石(抛灯泡)、电子秤找不足量金币、天平找重球、公司合并方案总数、海盗分赃等。
2-43.
从n元集合中取一个k元子集,并要求每个元素概率相等。若n未知又该如何解决?
解答:
原问题在http://www.cnblogs.com/wuyuegb2312/p/3141292.html#title3已经解答清楚了。
此文也解决了从未知行数中等概率选择一行的方法,那么如果需要选择k个呢?为了简化起见,限定未知的n>=k。那么先选择前k个元素;对第k+1个元素,以概率k/(k+1)选择之,并以等概率1/k代替已选择的k个元素中的一个。
这样,这一轮里前k个元素中某一个能留下的概率为1/(k+1) + [k/(k+1)] * [(k-1)/k] = k/(k+1)。那么对于第k+2个元素,类似地,以概率k/(k+2)选择之,并以等概率1/k代替已选择的k个元素中的一个,循环直至所有元素遍历结束。
(解答启发自http://blog.csdn.net/fall221/article/details/8805733)
2-44.
有1000份各不相同的数据项和1000个存储数据的结点,每个结点可以存放3份不同的数据项。制定一个备份方案,使其在某些结点失效时损失最小。当任意3个结点失效时,丢失的数据的期望数值是多少?
解答:
让所有结点存储内容不完全相同,是基本的。如果令结点n保存数据项n、n+1、n+2(取1000的模),最好情况是3个结点失效时不损失数据(各不连续或者2个连续),最坏情况是3个连续结点失效(n、n+1、n+2),损失n+2这一份数据。这个概率很容易计算,是1/10^(-6)。
相关延伸阅读:
RAID思想,保存异或结果,不过我算的概率相同:http://stackoverflow.com/questions/10291690/1000-items-1000-nodes-3-items-per-node-best-replication-scheme-to-minimize-da
类似的处理:http://blog.csdn.net/quietsound/article/details/9285375
2-45.
从n+1个数中找出最小数时,min = A[i]语句执行次数的期望。其中数组下标A[0...n]。
(首次赋值min=A[0]计算在内)
解答:
首先想到的是逆序对。但是通过序列[1,3,2]和[1,2,3]可知,两者赋值次数是一样的,显然与逆序对无关。
直接从期望入手,记E(n)为n+1个数时的该赋值语句期望执行次数。
最小的数在末尾A[n]的概率为1/n,这时需要一次赋值。
最小的数不在末尾A[n],则末尾处不需赋值,增加的赋值数为0。
这样,有E(n) = E(n-1) +1/n且E(0)=0。其中E(n-1)已经包括最小的数在非A[n]处的所有情况。因此E(n)为
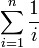
n比较大时,约为lnn。
(解答来自于:http://nbl.cewit.stonybrook.edu:60128/mediawiki/index.php/TADM2E_2.45)
2-46.
你有一栋100层高的大厦和2块大理石。你想找出一个最低楼层,从这个楼层开始,在它和比它更高的楼层上抛下大理石,落地会碎。如果有无限多块大理石,怎么最快找出这一层(抛的最少次数)?如果只有两块呢?(另一种说法:100层楼扔灯泡)
解答:
无限多块时,很容易想到用折半查找来进行。但是如果使用最少的大理石块又该如何找呢?注意到如果某次抛下时大理石未碎,那么下次仍能够使用。为了只用两块大理石来判断楼层数,由于碎裂的最低楼层是一定的,先做分析:
假设n是最多需要的测试次数(确定但未知,最坏情况),在第n层扔,如果碎了,由于只剩下一个灯泡,为了确定1至n-1层中哪一层,最坏情况是从1层一直扔到n-1层,共n-1次,加上之前的1次是n次,不超过n;如果未碎,那么上到2n-1层再扔,碎时同样有最坏情况从n+1层扔到2n-2层共n-2次,加上之前的是n次。依次类推,总结出每次测试都是n次,且确定的楼层范围是:n->2n-1->3n-2->...,即n + (n-1) + ... +1>100。求解使不等式成立的最小正整数是n=14。
(解答来自于:http://stackoverflow.com/questions/6547/two-marbles)
2-47.
有10袋金币,其中9袋中每个金币都是10克,另1袋中每个金币都是9克。给你一个能够数字显示重量的电子秤,找出全是9克的金币的那一袋。
解答:
看到称重量可能会联想到用天平找几堆商品中不足量的一份。可是这里用的是能显示具体数值的电子秤哎!如果还用天平的思想,可太死板了。
想想权重的概念,解法马上有了:从1号至10号袋中分别取1至10个金币,放到电子秤上。如果10袋全是10克的,那么应该显示550克;而缺几克,那就说明那个袋子里是9克的金币。一次解决,是不是很简单?
当然,权重也可以用别的方案分配,不过上面是最简单的。
(参考自:http://nbl.cewit.stonybrook.edu:60128/mediawiki/index.php/TADM2E_2.47)
2-48.
8个外表一样的球,其中7个等重,另1个比它们重。用天平在2次的比较后找出这个重球。
解答:
由于有“2次比较”的提示,这个就简单了:把球分为(1,2,3),(4,5,6),(7,8)三组,第一次称(1,2,3)和(4,5,6),若一组重,那么将3个中取2个可得重的是这2个之一还是其余一个;否则将(7,8)称重。
如果按这个思路,9个球也能够解决。
2-49.
将n个公司合并成1个公司,一共有几种不同的方式合并?
解答:
记合并方式f(n)种,f(n)=f(n-1)*g(n),其中g(n)是将n个公司通过一次合并变为n-1个公司的方法。显然g(n)为组合数C(n,2)。递推公式解得
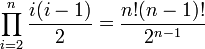
(参考自http://nbl.cewit.stonybrook.edu:60128/mediawiki/index.php/TADM2E_2.49)
2-50.
Rramanujan数是可以写作a^3+b^3=c^3+d^3的数,其中a!=c且b!=d,或者a!=d且b!=c。找出满足所有给定小于n的Rramanujan数。
解答:
编程实现如下
#include<stdio.h> int main() { int n, i, count=0, j, k, int_count; printf("Enter the number of values needed: "); scanf("%d", &n); i = 1; while(count < n) { int_count = 0; for (j=1; j<=((int(pow(i, 1.0/3)); j++) { for(k=j+1; k<=((int(pow(i,1.0/3)); k++) { if(j*j*j+k*k*k == i) int_count++; } } if(int_count == 2) { count++; printf(" Got %d Hardy-Ramanujan numbers %d", count, i); } i++; } }
注意几点以加速搜索:
确保j<k,这样另一对j、k与原来的必然互不相等;
两个for循环终止条件是j^3<i。
(参考自:http://stackoverflow.com/questions/11410798/finding-hardy-ramanujan-numbers)
2-51.
6个海盗分300美刀,分赃方法如下:有由资历最深的提出分配方案,进行投票。如果获得半数及以上支持,那么按照他的分配方案进行;否则,其他海盗杀掉他,资历第二深的海盗来提出分配方案,其后仍要投票表决,依次类推。请分析分配方法。(所有海盗都以自己存活为最优考虑,保证存活的条件下才尽可能希望多获得美刀。)
解答:
将海盗按资历有深到浅编号为1,2,3,4,5,6。假设只剩下5,6两个海盗时,5无论提出怎样的分配方案,都能使支持过半(自己的一票),那么分配方法必然是:
(5,6) ---->(300,0)
时间倒流,加入海盗4。海盗4为了防止投票不过半而被杀死,需要拉拢海盗6。由于6在上一种情况里什么也分不到,这时只要4分给6,无论多少,6都会同意。这样,4给他最少的数目,即1。而5希望进入下一轮投票,因此只有给他全部300刀才能拉拢。由于投票已过半(2/3),不必拉拢5。此时分配方案为:
(4,5,6) ---->(299,0,1)
加入海盗3时,出于类似的考虑,提出这样的方案:
(3,4,5,6) ---->(299,0,1,0),这样能拉拢5,不至于3死后,5什么也分不到。
(299,1,0,0)必然不能拉拢4,因为将3干掉后4能获得299。至于为什么不用(299,0,0,1)这样的方案呢?此时6无论是否同意,他都有机会在本轮获得1美刀或者把3干掉后的下一轮必然获得1美刀。因此3的幸存与否是未知的,他不能做出这种使自己生命可能受到威胁的分配方式。后面的分析类似。有:
(2,3,4,5,6) --->(298,0,1,0,1)
(1,2,3,4,5,6) ----> (298,0,1,0,1,0)
(参考自:http://nbl.cewit.stonybrook.edu:60128/mediawiki/index.php/TADM2E_2.51,这里我补充了不少分析。)
2.52.
如果2.51中只有1美刀来分赃,谁会得到它,在这个分配过程中会死多少人?
解答:
和上一题分析类似,当只有2个海盗时,年长那个一定能得到那1美刀;当海盗数大于等于3时,任何分配给自己的分配方案都不能保证自己一定能存活,不如直接分给倒数第二个海盗。(但即使如此,也可能被杀死。投票将演化成杀死一部分海盗,然后让倒数第二个海盗获得的过程。)
(更一般的情况请参考http://en.wikipedia.org/wiki/Pirate_game。注意,中文wiki上没有详细的扩展情况的介绍。)