全景拼接学习-原理篇 (1) 两张图片之间关系计算 单应性Homograph估计

教程 https://zhuanlan.zhihu.com/p/74597564

 目录
一 图像变换与平面坐标系的关系
二 平面坐标系与齐次坐标系
三 单应性变换

一 图像变换与平面坐标系的关系

• 旋转：

 

 

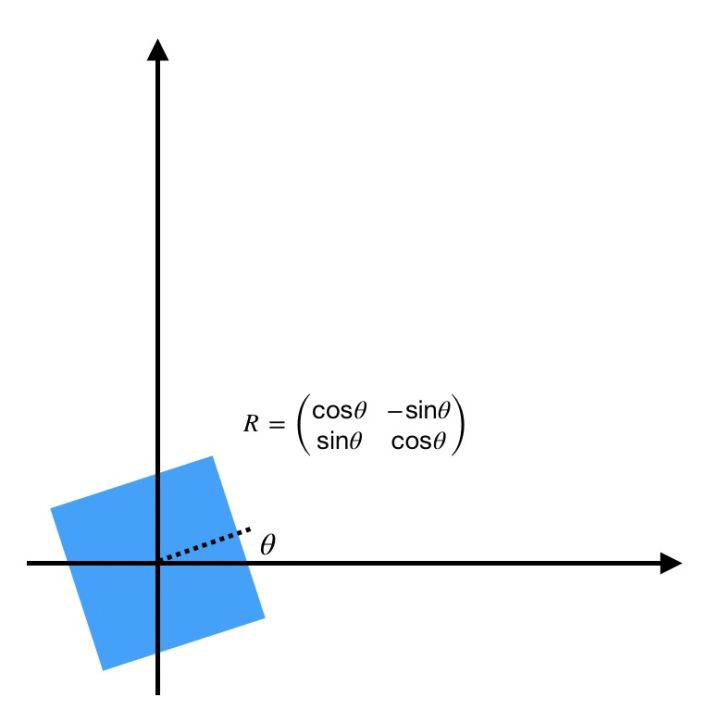
 写成矩阵乘法形式：

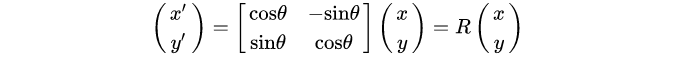
• 平移：

 

 

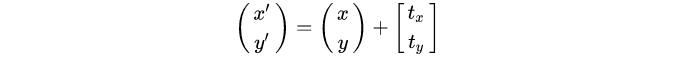
 但是现在遇到困难了，平移无法写成和上面旋转一样的矩阵乘法形式。所以引入齐次坐标  ，再写成矩阵形式：

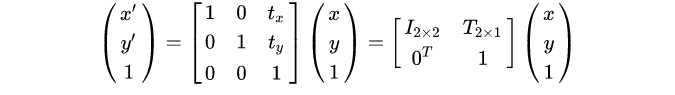
 其中  表示单位矩阵，而  表示平移向量。

那么就可以把把旋转和平移统一写在一个矩阵乘法公式中，即刚体变换：

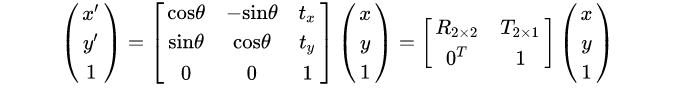
 而旋转矩阵  是正交矩阵（  ）。

刚体变换：旋转+平移（正方形-正方形）

作用：z轴距离不变 x  y 和原来相等  

仿射变换

作用：z轴距离不变 x  y 各自被比例拉伸 

 

 其中  可以是任意2x2矩阵（与  一定是正交矩阵不同）。

 仿射变换（正方形-平行四边形）

可以看到，相比刚体变换（旋转和平移），仿射变换除了改变目标位置，还改变目标的形状，但是会保持物体的“平直性”。

不同  和  矩阵对应的各种基本仿射变换：

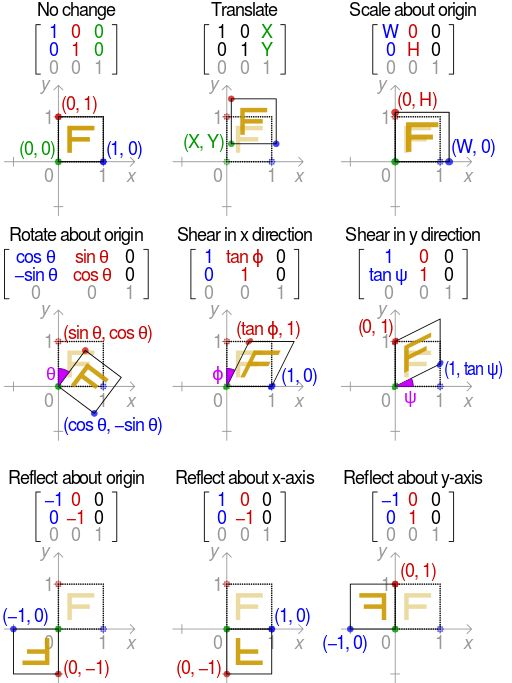
仿射变换（正方形-平行四边形）

 可以看到，相比刚体变换（旋转和平移），仿射变换除了改变目标位置，还改变目标的形状，但是会保持物体的“平直性”。

不同  和  矩阵对应的各种基本仿射变换：

 

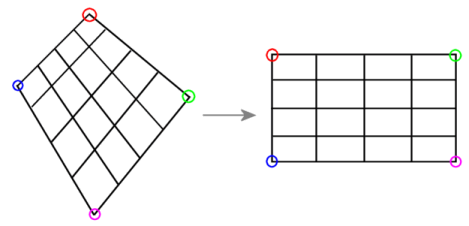
• 投影变换（单应性变换）

投影变换（单应性变换）

作用：z轴距离被拉伸   x  y 被比例拉伸  z

 

 

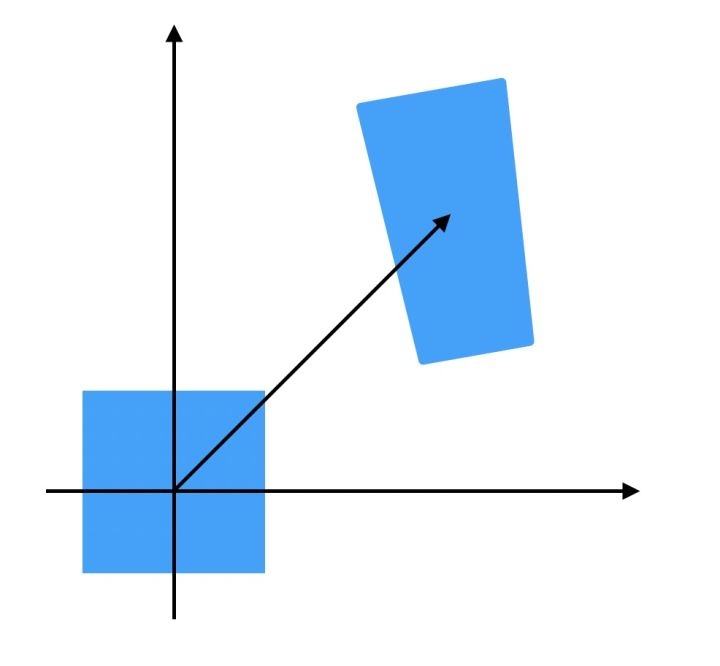
 投影变换（正方形-任意四边形）

总结一下：

1. 刚体变换：平移+旋转，只改变物体位置，不改变物体形状  x y  z等于原来
2. 仿射变换：改变物体位置和形状，但是保持“平直性”    z不变  x y 被比例拉伸
3. 投影变换：彻底改变物体位置和形状                         z  x y 都被比例拉伸

 

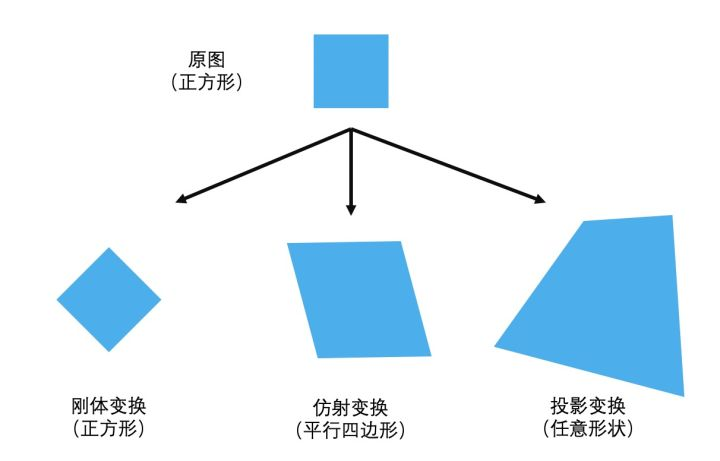
 注：上图“投影变换”应该是“任意四边形”

我们来看看完整投影变换矩阵各个参数的物理含义：

 

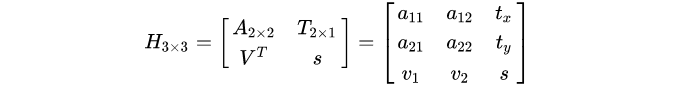
 其中  代表仿射变换参数

  代表平移变换参数

  表示一种“变换后边缘交点“关系，如：

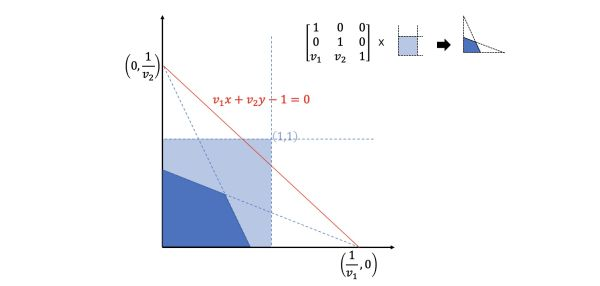
至于  则是一个与  相关的缩放因子。

一般情况下都会通过归一化使得  （原因见下文）。

二 平面坐标系与齐次坐标系

问题来了，齐次坐标到底是什么？

齐次坐标系  与常见的三维空间坐标系  不同，只有两个自由度：

而  （其中  ）对应坐标  和  的缩放尺度。当  时：

特别的当  时，对应无穷远：

三 单应性变换

• 单应性是什么？

此处不经证明的给出：同一个 [无镜头畸变] 的相机从不同位置拍摄 [同一平面物体] 的图像之间存在单应性，可以用 [投影变换] 表示 。

注意：单应性成立是有条件的！

简单说就是：

其中  是Left view图片上的点，  是Right view图片上对应的点。

• 那么这个  单应性矩阵如何求解呢？

更一般的，每一组匹配点  有

由平面坐标与齐次坐标对应关系  ，上式可以表示为：

进一步变换为：

写成矩阵  形式：

也就是说一组匹配点  可以获得2组方程。

• 单应性矩阵8自由度

注意观察：单应性矩阵  与  其实完全一样（其中 ），例如：

即点  无论经过  还是  映射，变化后都是  。

如果使  ，那么有:

所以单应性矩阵  虽然有9个未知数，但只有8个自由度。

在求  时一般添加约束  （也有用  约束），所以还有  共8个未知数。由于一组匹配点  对应2组方程，那么只需要  组不共线的匹配点即可求解  的唯一解。

 

可以看到：

1. 红框所在平面上内容基本对齐，但受到镜头畸变影响无法完全对齐；
2. 平面外背景物体不符合单应性原理，偏离很大，完全无法对齐。

• 传统方法估计单应性矩阵

一般传统方法估计单应性变换矩阵，需要经过以下4个步骤：

1. 提取每张图SIFT/SURF/FAST/ORB等特征点
2. 提取每个特征点对应的描述子
3. 通过匹配特征点描述子，找到两张图中匹配的特征点对（这里可能存在错误匹配）
4. 使用RANSAC算法剔除错误匹配
5. 求解方程组，计算Homograph单应性变换矩阵

样例1  输入两张图+特征检测+自动匹配+自动求解单应矩阵+根据单应矩阵变换图像+输出拼接图

　　

 opencv 349+vs2015 opencv编译了扩展库及其sfft库  使用sift角点

#include <iostream>
#include <vector>
#include <opencv2/core.hpp>
#include <opencv2/imgproc.hpp>
#include <opencv2/highgui.hpp>
#include <opencv2/features2d.hpp>
#include <opencv2/calib3d.hpp>
#include <opencv2/xfeatures2d.hpp>
#include <opencv2/stitching.hpp>

#define PARLIAMENT01 "x1.bmp"
#define PARLIAMENT02 "x2.bmp"

using namespace cv;
using namespace std;

int main()
{
	Mat image1 = imread(PARLIAMENT01, 0);
	Mat image2 = imread(PARLIAMENT02, 0);
	if (!image1.data || !image2.data)
		return 0;

	//namedWindow("Image 1", 1);
	//namedWindow("Image 2", 1);
	//imshow("Image 1", image1);
	//imshow("Image 2", image2);

	vector<KeyPoint> keypoints1;
	vector<KeyPoint> keypoints2;
	Mat descriptors1, descriptors2;

	//创建SIFT检测器
	Ptr<Feature2D> ptrFeature2D = xfeatures2d::SIFT::create(74);

	//检测SIFT特征并生成描述子
	ptrFeature2D->detectAndCompute(image1, noArray(), keypoints1, descriptors1);
	ptrFeature2D->detectAndCompute(image2, noArray(), keypoints2, descriptors2);

	cout << "Number of feature points (1): " << keypoints1.size() << endl;
	cout << "Number of feature points (2): " << keypoints2.size() << endl;

	//使用欧氏距离和交叉匹配策略进行图像匹配
	BFMatcher matcher(NORM_L2, true);
	vector<DMatch> matches;
	matcher.match(descriptors1, descriptors2, matches);

	Mat imageMatches;
	drawMatches(image1, keypoints1,  // 1st image and its keypoints
		image2, keypoints2,  // 2nd image and its keypoints
		matches,            // the matches
		imageMatches,       // the image produced
		Scalar(255, 255, 255),  // color of the lines
		Scalar(255, 255, 255),  // color of the keypoints
		vector<char>(),
		2);

//	namedWindow("Matches (pure rotation case)", 0);
//	imshow("Matches (pure rotation case)", imageMatches);

	//将keypoints类型转换为Point2f
	vector<Point2f> points1, points2;
	for (vector<DMatch>::const_iterator it = matches.begin();
		it != matches.end(); ++it)
	{
		float x = keypoints1[it->queryIdx].pt.x;
		float y = keypoints1[it->queryIdx].pt.y;
		points1.push_back(Point2f(x, y));

		x = keypoints2[it->trainIdx].pt.x;
		y = keypoints2[it->trainIdx].pt.y;
		points2.push_back(Point2f(x, y));
	}

	cout << "number of points: " << points1.size() << " & " << points2.size() << endl;

	//使用RANSAC算法估算单应矩阵
	vector<char> inliers;
	Mat homography = findHomography(
		points1, points2, // corresponding points
		inliers,         // outputed inliers matches
		RANSAC,      // RANSAC method
		1.);             // max distance to reprojection point

						 //画出局内匹配项
	drawMatches(image1, keypoints1,  // 1st image and its keypoints
		image2, keypoints2,  // 2nd image and its keypoints
		matches,            // the matches
		imageMatches,       // the image produced
		Scalar(255, 255, 255),  // color of the lines
		Scalar(255, 255, 255),  // color of the keypoints
		inliers,
		2);

	namedWindow("Homography inlier points", 0);
	imshow("Homography inlier points", imageMatches);

	//用单应矩阵对图像进行变换
	Mat result;
	warpPerspective(image1, // input image
		result,         // output image
		homography,     // homography
		Size(2 * image1.cols, image1.rows)); // size of output image

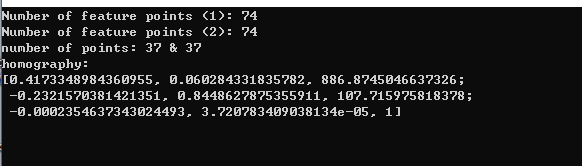
	cout << "homography:" << endl;
	cout << homography << endl;
											 //拼接
	Mat half(result, Rect(0, 0, image2.cols, image2.rows));
	image2.copyTo(half);
	namedWindow("Image mosaic", 0);
	imshow("Image mosaic", result);

	waitKey();
	return 0;
}

　

　样例2  变换矩阵如何实现变换  

上面是调用库函数实现，从源码查看自己怎么实现

dst(x,y) = src((M11x+M12y+M13)/(M31x+M32y+M33), (M21x+M22y+M23)/(M31x+M32y+M33))

 - void mywarpPerspective(Mat src,Mat &dst,Mat T) {


   //此处注意计算模型的坐标系与Mat的不同

   //图像以左上点为（0,0），向左为x轴，向下为y轴，所以前期搜索到的特征点 存的格式是（图像x，图像y）---（rows，cols）

   //而Mat矩阵的是向下为x轴，向左为y轴，所以存的方向为（图像y，图像x）----（cols，rows）----（width，height）

   //这个是计算的时候容易弄混的


   //创建原图的四个顶点的3*4矩阵（此处我的顺序为左上，右上，左下，右下）

       Mat tmp(3, 4, CV_64FC1, 1);
       tmp.at < double >(0, 0) = 0;
       tmp.at < double >(1, 0) = 0;
       tmp.at < double >(0, 1) = src.cols;
       tmp.at < double >(1, 1) = 0;
       tmp.at < double >(0, 2) = 0;
       tmp.at < double >(1, 2) = src.rows;
       tmp.at < double >(0, 3) = src.cols;
       tmp.at < double >(1, 3) = src.rows;

   //获得原图四个顶点变换后的坐标，计算变换后的图像尺寸
       Mat corner = T * tmp;      //corner=(x,y)=(cols,rows)
       int width = 0, height = 0;
       double maxw = corner.at < double >(0, 0)/ corner.at < double >(2,0);
       double minw = corner.at < double >(0, 0)/ corner.at < double >(2,0);
       double maxh = corner.at < double >(1, 0)/ corner.at < double >(2,0);

       double minh = corner.at < double >(1, 0)/ corner.at < double >(2,0);
       for (int i = 1; i < 4; i++) {
           maxw = max(maxw, corner.at < double >(0, i)  /  corner.at < double >(2, i));
           minw  = min (minw,  corner.at < double >(0, i)  /  corner.at < double >(2, i));
           maxh  = max(maxh, corner.at < double >(1, i)  /  corner.at < double >(2, i));
           minh  = min (minh,   corner.at < double >(1, i)  /  corner.at < double >(2, i));

       }

   //创建向前映射矩阵 map_x, map_y


         //size(height,width)
       dst.create(int(maxh - minh), int(maxw - minw), src.type());
       Mat map_x(dst.size(), CV_32FC1);
       Mat map_y(dst.size(), CV_32FC1);

       Mat proj(3,1, CV_32FC1,1);

       Mat point(3,1, CV_32FC1,1);

      T.convertTo(T, CV_32FC1);  
   //本句是为了令T与point同类型（同类型才可以相乘，否则报错，也可以使用T.convertTo(T, point.type() );）
   Mat Tinv=T.inv();   

       for (int i = 0; i < dst.rows; i++) {        
           for (int j = 0; j < dst.cols; j++) {
               point.at<float>(0) = j + minw ;
               point.at<float>(1) = i + minh ;
               proj = Tinv * point;
               map_x.at<float>(i, j) = proj.at<float>(0)/ proj.at<float>(2) ;
               map_y.at<float>(i, j) = proj.at<float>(1) / proj.at<float>(2) ;
           }
       }
       remap(src,dst,map_x,map_y, CV_INTER_LINEAR);


   }