C2 Register Allocation

0. 参考

主要参考：
http://cr.openjdk.java.net/~thartmann/offsite_2018/register_allocator.pdf
​

https://wiki.openjdk.java.net/display/HotSpot/The+C2+Register+Allocator
​

https://wiki.openjdk.java.net/display/HotSpot/C2+Register+Allocator+Notes
​

https://ssw.jku.at/Research/Papers/Wimmer04Master/Wimmer04Master.pdf
​

1. 图染色寄存器分配算法

一点翻译，来自C.W.的研究生论文，附带一点我的私货。

目前最常见的方法是将寄存器分配问题视作图染色问题。第一个实现G.J.Chaitin做出的，接着P.Briggs对它做了些提升，C2的寄存器分配(以下可能简称RA)几乎遵照Briggs-Chaitin style实现。

1.1 构造干扰图

图染色的目的是给每个虚拟寄存器（virtual register）赋予一个物理寄存器（physical register）。每个虚拟寄存器都有一个live range，始于值第一次定义，终于值最后一次使用。live range不必是连续的，它允许出现空洞，因为可能存在重复定义和使用。
​

N个虚拟寄存器必须映射到R个物理寄存器上，N通常比R大得多。物理寄存器就是“颜色”，要“染”的东西是寄存器干扰图，这个图中的节点就是虚拟寄存器。如果两个节点有一条边连接，那么这两个节点（虚拟寄存器）必须使用不同的颜色染（物理寄存器），以保障同一时刻一个物理寄存器只对应一个虚拟寄存器。
​

Fig2.1有个简单的例子，包括五个虚拟寄存器v1，v2，v3，v4，v5，假设只有两个物理寄存器r1，r2。指令有七条，右边是它们各自的live range。v1从(1)开始，(7)结束，因为它在(1)定义在(7)最后一次使用。因为(5)重复定义，所以(3)-(5)出现了空洞。

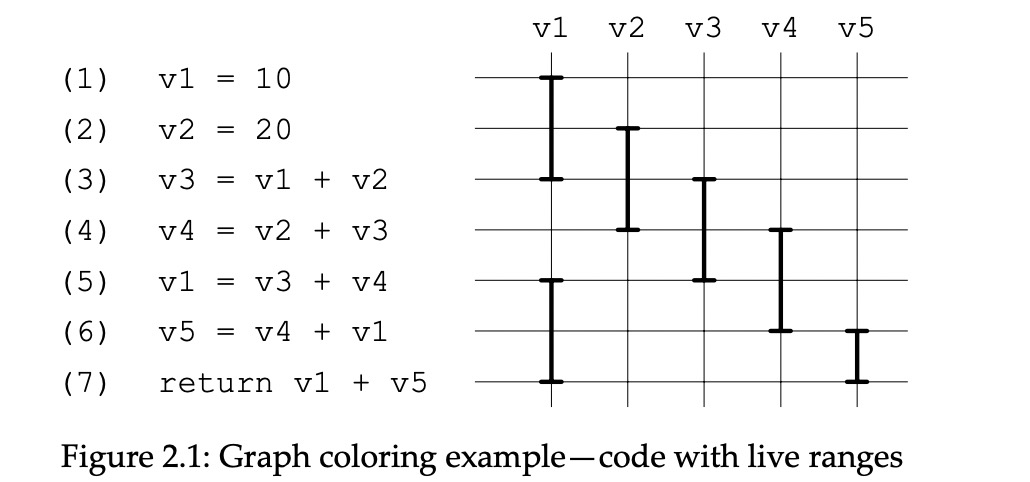
v1在(1)定义，(3)使用。因为v2在(2)处定义，它干扰了v1 live range，所以v1 v2两个节点连线。同理，v1在(5)处干扰v4，所以v1 v4连线。v5干扰v1，v5 v1连线。v4干扰v3，v3 v4连线。如此继续，最终形成Fig2.2的寄存器干扰图。

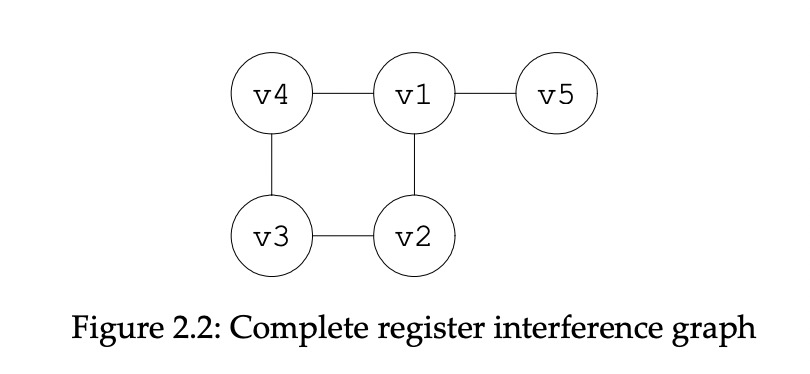
1.2 修剪干扰图

现在寄存器干扰图必须被R个颜色染色，并且连线的两个节点必须染不一样的颜色，让它们拿到不同的物理寄存器。穷尽出染色的所有方案是不可行的，因为这是个已知的NP完全问题。我们用迭代的方案，来简化图。如果找不到染色方案就说明有些虚拟寄存器必须spill到内存。需要一个成本函数来找出哪些值spill到内存对性能的影响最小。
​

要想对干扰图染色，可以迭代式修剪图。每次迭代移除选择的节点和所有关联边，然后放到栈上。选择哪个节点取决于两条规则：
1） 如果图包含一个节点，它的度小于R（即节点关联边少于R），那么当且仅当没有这个节点的剩下的图是可染色的，该节点才是可染色的。如果剩下的图最后成功染色，那么总能找到一个染色给当前节点染色，因为当前节点关联边小于度R，既然剩下染成功了，那么它们不可能拿到所有颜色，至少有一个可用颜色。为啥可以这样呢？之前也说过了，只要关联节点不染同一个颜色，当前节点就是可染色的（colorable）。
2）用成本函数选择最不重要的节点，从图中移除并让到栈上。即使所有节点的度都高于R，也可以通过这条规则继续染色。
​

先用第一条规则，移除度为1的v5放到栈上。然后剩下所有节点度都等于2，假设成本函数选了v2，移除v2放栈上。接着用第一条规则选v3，移除v3放栈上。在用第一条规选v1，移除放栈上。最后选v4，移除放栈上。

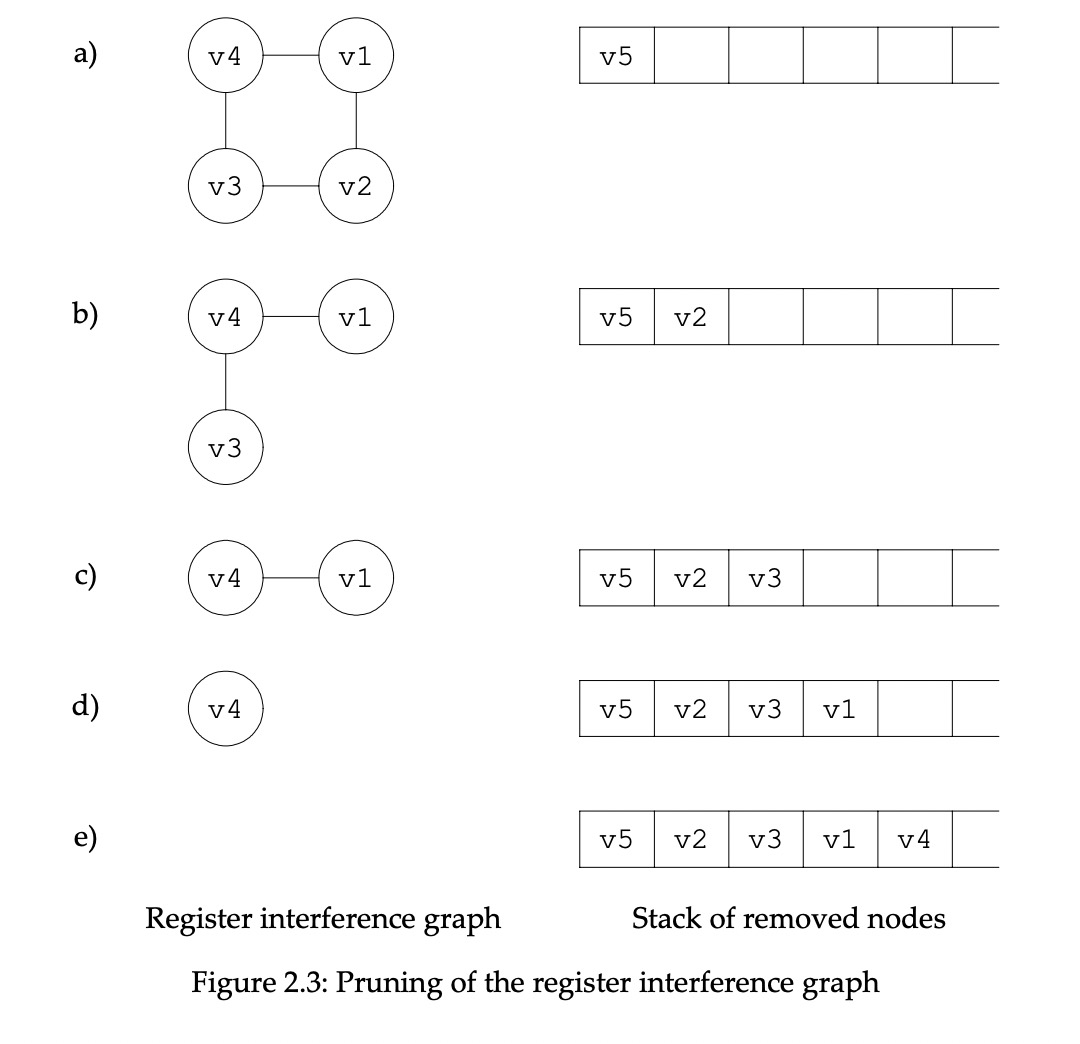
1.3 重建干扰图

这一步我们从栈上pop节点，根据之前的边重建干扰图，重建的时候会给节点染上色，只要关联节点没有用到的颜色都可以选。如果这个时候找不到可用颜色，那么这个虚拟寄存器需要标记为spilling。当所有节点处理完毕，并且假设没有spilling节点，那么该图已经完全被染色，每个虚拟寄存器都可以替换为颜色对应的物理寄存器。如果需要spilling，将插入对应的spilling代码到IR中，因为这个spilling代码本身也需要寄存器，所有需要再来一次算法，即构造新的干扰图、修剪、重构，直到最后没有spilling，图被完全染色。
​

重建过程如Fig2.4所示：pop v4，染r1。pop v1，染r2。pop v3，染r2。pop v2，染r1。pop v5染r1。此时图完全染色，算法结束。

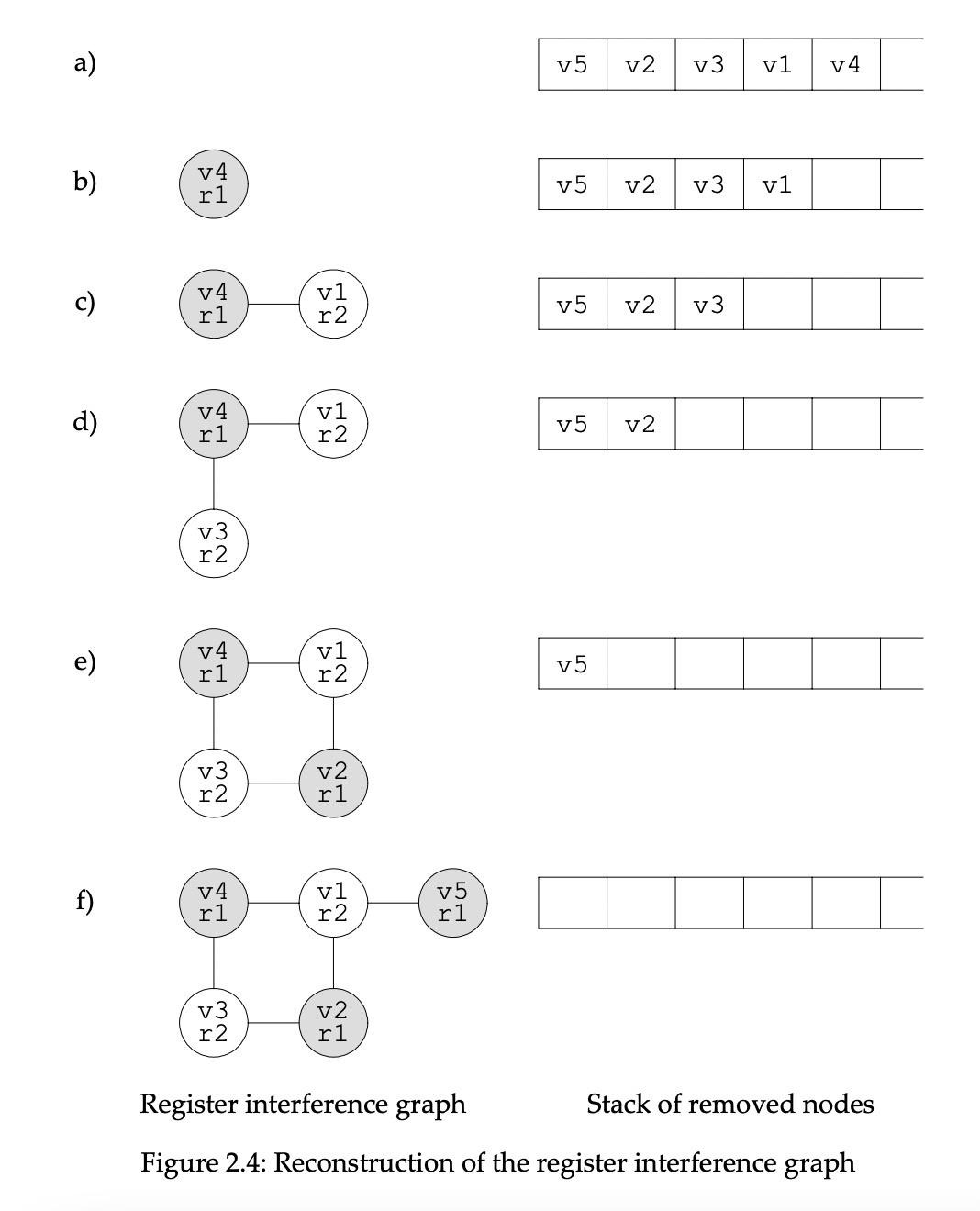
用染色结果代替之前的IR，如图Fig2.5所示：

2. RA实现概览

由于Niclas Adlertz的slide已经很直白了，我不一定做的比他好，所以以他的slide为主，附上一些解释，以及补充。

回顾之前的算法，有几个关键点：

• 干扰图的节点表示变量（虚拟寄存器）
• 干扰图的颜色表示寄存器（物理寄存器）
• 关联节点不能同一时刻染同一颜色（同一时刻这些变量不能同时存活）

Chaitin算法一些核心流程如下：

• Build IFG: 使用live range数据构造干扰图（Interference graph，IFG）
• Simplify: 从IFG移除节点，放到栈上
  • 规则1: degree<R，
  • 规则2:degree>=R
• Spill：如果必须Spill，插入spill代码，然后算法重来
• Select：从栈pop所有节点，重建IFG，期间给节点染色，要求选的颜色不能是关联节点已经选的

Chaitin完整流程如下：

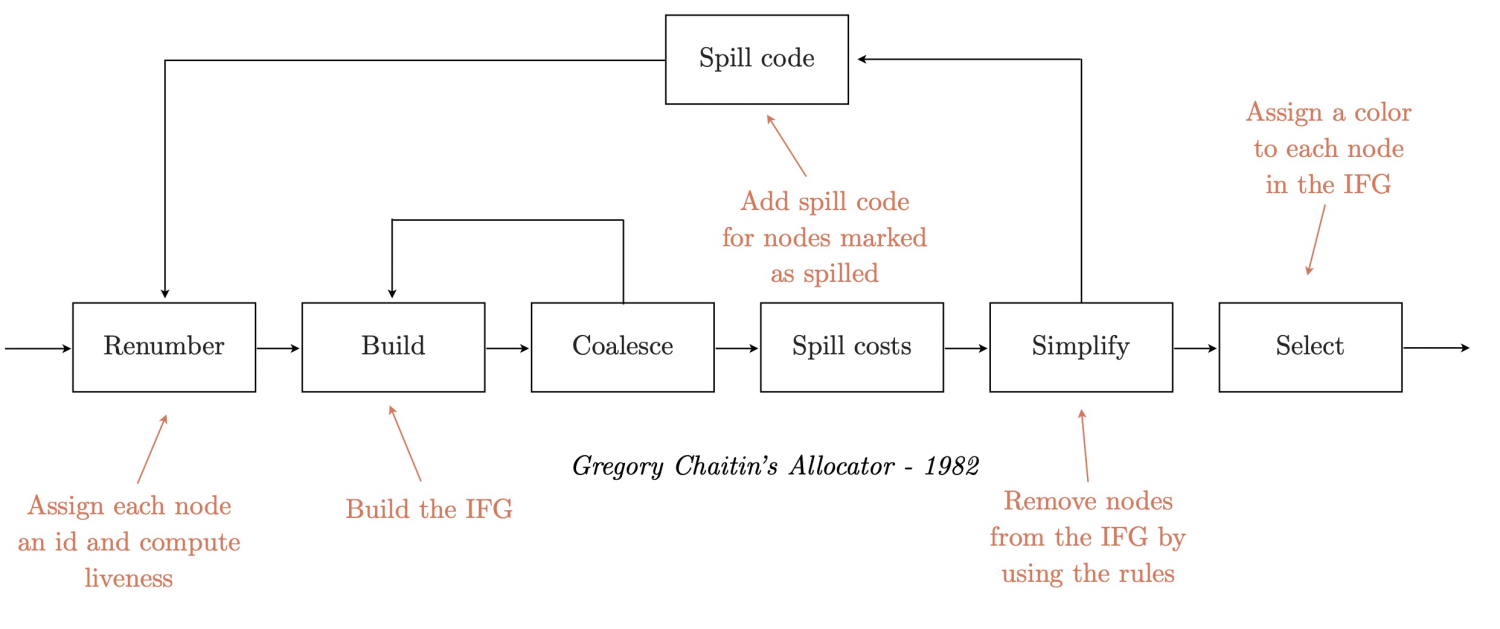
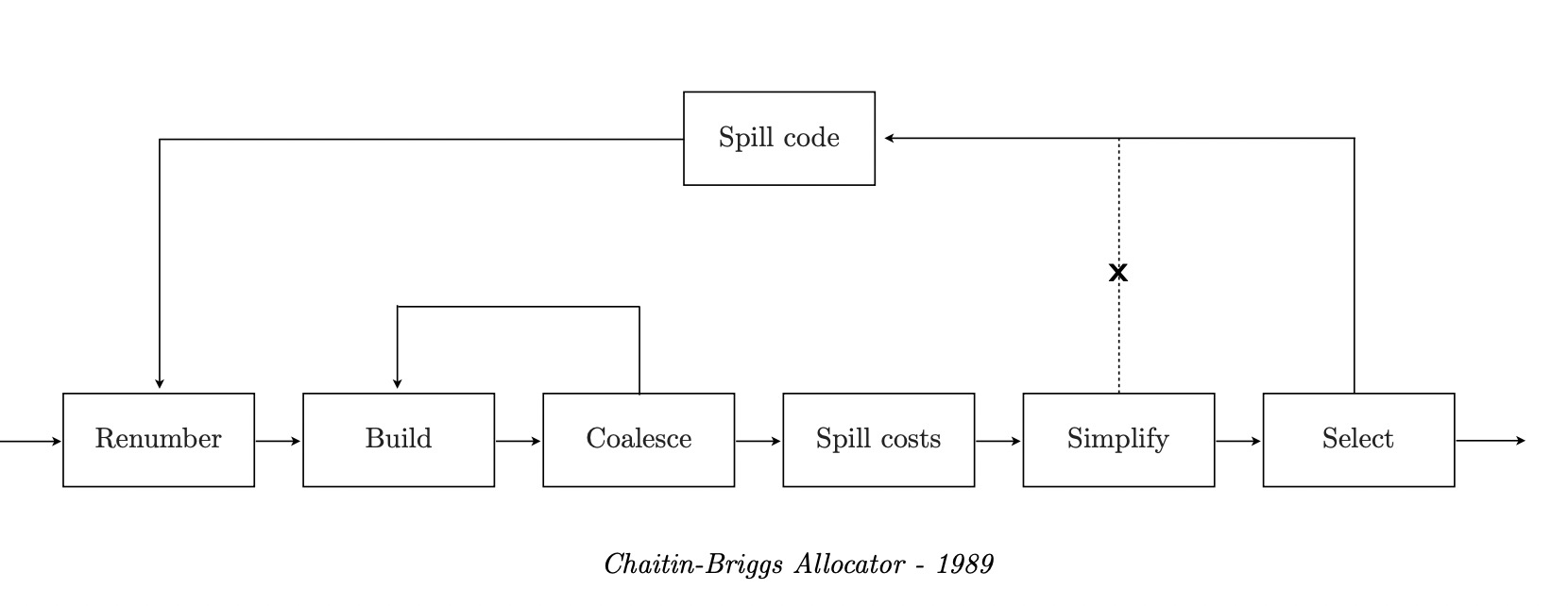
注意上面说的是Chaitin算法，Briggs还做了一些改进，而C2用的是Briggs-Chaitin算法。改进如下：

• 即使Simplify不能用第一条规则给所有节点染色，也尝试在Select节点染色。
• Chaitin能染色的该算法能，Chaitin不能染色的该算法部分能。

3. C2 RA实现

3.0 Overview

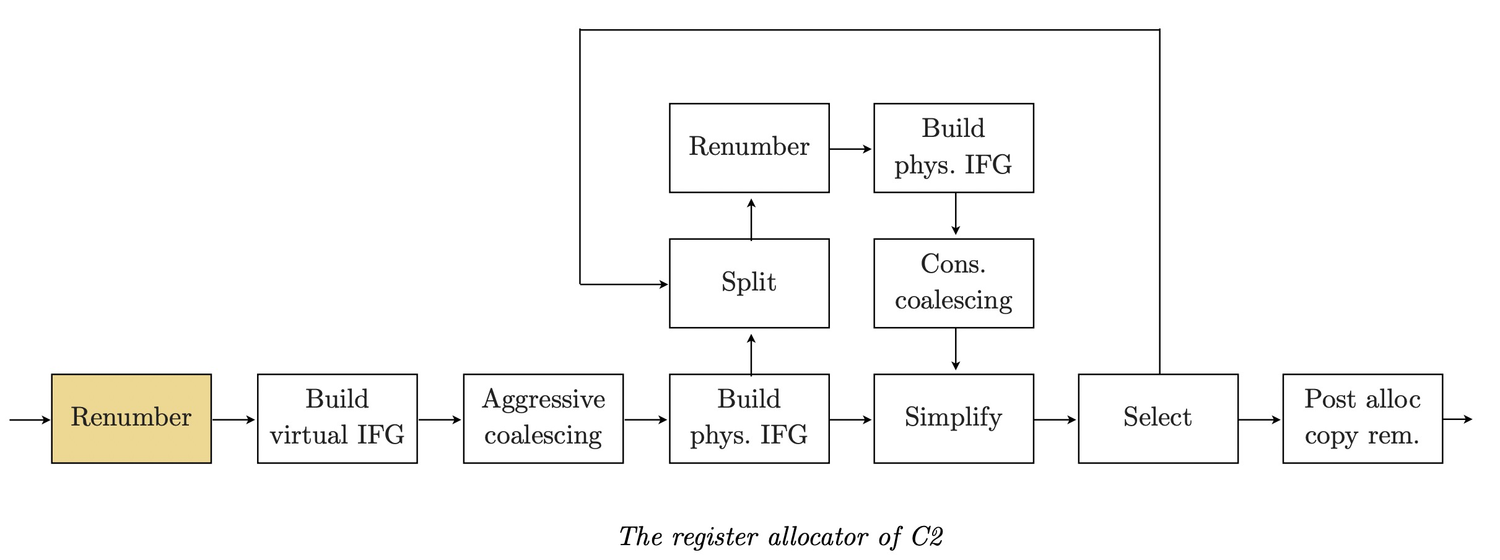
3.1 Renumber

3.1.1 收集LRG

这一步我理解为每个指令生成LRG(Live RanGe)数据结构，LRG包含很多东西，比如选择的寄存器(_reg)，允许使用哪些寄存器(_mask)，寄存器压力(_reg_pressure)，需要多少个寄存器来表达这个数据(_num_regs)。这些信息的收集由PhaseChaitin::gathe_lrg_masks完成，实现也很简单，遍历所有block的每个node，然后处理node，接着再处理node所有的input。

3.1.2 计算live out

搜集完所有指令的lrg之后，接着是指令live_out/live_gen(use)/live_kill(def)的计算，在PhaseLive::compute里面完成，熟悉C1寄存器分配的朋友对这过程应该不会陌生。这是个反向数据流传播问题。
​

3.2 Build virtual IFG

构造虚拟寄存器的IFG这步还比较简单。这一步遍历所有指令，然后检查当前指令_mask和live_out里面指令_mask是否重叠，_mask之前说了表示指令可能用到的所有寄存器，这一步就是说当前指令可能用到的所有寄存器是否和live out里面指令所有可能用到的寄存器是否有重叠，有重叠表示它们可能同时存活，即两者干扰。

void PhaseChaitin::build_ifg_virtual( ) {
  // 遍历所有block
  for (uint i = 0; i < _cfg.number_of_blocks(); i++) {
    Block* block = _cfg.get_block(i);
    IndexSet* liveout = _live->live(block);
    // 遍历当前block的所有node，即instruction
    for (uint j = block->end_idx() + 1; j > 1; j--) {
      Node* n = block->get_node(j - 1);
      // 拿到当前节点的lrg id（live range id）
      uint r = _lrg_map.live_range_id(n);
      // 如果存在live range
      if (r) {
        // 从live-out移除当前节点
        liveout->remove(r);
        ...
        // 求干扰图
        interfere_with_live(r, liveout);
      }

      // 如果当前node不是Phi，遍历当前node的所有input node
      if (!n->is_Phi()) {
        for(uint k = 1; k < n->req(); k++) {
          // 在live-out插入input node
          liveout->insert(_lrg_map.live_range_id(n->in(k)));
        }
      }
      ...
    }
  }
}
void PhaseChaitin::interfere_with_live(uint lid, IndexSet* liveout) {
  if (!liveout->is_empty()) {
    LRG& lrg = lrgs(lid);
    const RegMask &rm = lrg.mask();
    // 遍历live_out
    IndexSetIterator elements(liveout);
    uint interfering_lid = elements.next();
    while (interfering_lid != 0) {
      LRG& interfering_lrg = lrgs(interfering_lid);
      // 如果当前lrg id和liveout某个lrg id生命周期重叠，那么两者存在干扰
      if (rm.overlap(interfering_lrg.mask())) {
        // 在干扰图上连接两个node
        _ifg->add_edge(lid, interfering_lid);
      }
      interfering_lid = elements.next();
    }
  }
}

3.3 Aggressive coalescing

3.3.1 合并Phi/2-address指令及其输入

到这里IR存在一些virtual copy。所谓virtual copy是指我们没有真的复制代码，只是把变量作为phi的输入。phi本身有一个单独的live range，这一步的目的就是合并这些输入和phi，让它们具有相同的生命周期，如果没法合并，那就等下插入真正的copy代码。
​

所谓2-address就是指只有一个input，一个output的指令，比如最典型的mov eax,ebx。

void PhaseCoalesce::coalesce_driver() {
  // 遍历所有block
  for (uint i = 0; i < _phc._cfg.number_of_blocks(); i++) {
    coalesce(_phc._blks[i]);
  }
}
void PhaseAggressiveCoalesce::coalesce( Block *b ) {
  // 遍历successor
  uint i;
  for( i=0; i<b->_num_succs; i++ ) {
    Block *bs = b->_succs[i];
    ...
    // 遍历successor的所有Phi
    for( uint k = 1; k<bs->number_of_nodes(); k++ ) {
      Node *n = bs->get_node(k);
      if( !n->is_Phi() ) break;
      // 合并这些Phi和它的input
      combine_these_two( n, n->in(j) );
    }
  }
  // 寻找2-address指令，然后合并
  uint cnt = b->end_idx();
  for( i = 1; i<cnt; i++ ) {
    Node *n = b->get_node(i);
    uint idx;
    if (n->is_Mach() && (idx = n->as_Mach()->two_adr())) {
      MachNode *mach = n->as_Mach();
      combine_these_two(mach, mach->in(idx));
    }
  }
}

3.3.2 插入真正的copy

如果不能合并phi和它的输入，那就插入真的copy指令（2-address指令同理）。

3.4 Build phys. IFG

to write, to learn