组成原理（十）：运算及ALU

目录

• 学习重点
• 1.定点运算
  • 1.1 移位运算
  • 1.2 加减运算
  • 1.3 乘法
  • 1.4 除法
• 2.浮点加减运算
  • 2.1 对阶
  • 2.2 尾数求和
  • 2.3 (尾数)规格化
  • 2.4 舍入
  • 2.5 溢出判断
• 3.ALU
  • 3.1 进位链

学习重点

• 定点运算
  • 移位运算
  • 加减运算
  • 乘法
  • 除法
• 浮点运算
  • 加减
• ALU
  • 示意图
  • 并行加法器
    • 串行快速进位链
    • 并行快速进位链

1.定点运算

1.1 移位运算

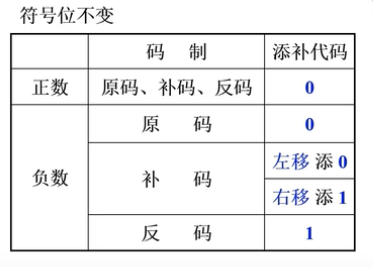
1. 算术移位规则：
   符号位不动，其他位移动，添补代码如下：

   • 正数：原反补码，都补0
   • 负数：
     • 源码，补0
     • 反码，补1
     • 补码，左0右1

2. 规则示意图：
   

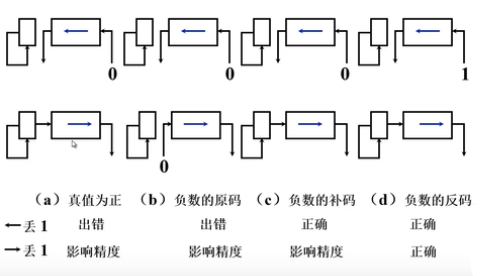
3. 算术移位与逻辑移位：

   • 算术移位：有符号位的移位(考虑符号位)
   • 逻辑移位：无符号位的移位(符号位一起移动)
   • 逻辑左移：低位添0，高位丢失
   • 逻辑右移：高位添0，低位丢失

4. 移位硬件实现：
   

1.2 加减运算

1. 公式：连同符号位一起计算

   • [A]补+[B]补=[A+B]补
   • [A]补+[(-B)]补=[A-B]补

2. 溢出判断：(进位不等于溢出)

   • 溢出：结果超出表示范围
     • 定点小数和>1
     • 整数和符号位进位可能溢出
   • 一位符号位判断：仅考虑进位的符号
     • 进位符号与原符号不同，则溢出
     • 需要相加的两个数符号位相同才能判断
   • 两位符号位判断：进位后产生的两个符号位A,B

     • 若A⊕B=1，则溢出（不同溢）

     • 若A⊕B=0，则未溢出（同不溢）

     • 如：1,0111+1,1011 相加不溢出
       

     • 最高符号位代表真正符号位

3. 加减法硬件配置
   

   • V：溢出标记
   • A，X：寄存器，A就是ACC
     • A：ACC，保存被加数及和，被减数及差
     • X：X寄存器，保存加数或减数
     • A与X均为n+1位
   • GA：加法控制，加法置1
   • GS：减法控制，减法置1
   • 减法操作时部控制逻辑启用
     • 完成从[B]补到[-B]补的转换
   • 加法：A+X—>A
   • 减法：A+(-X)—>A

1.3 乘法

1. 笔算乘法：
   

   • 符号由异或决定

2. 乘法竖式表示：
   A：-0.1101，被乘数
   B：0.1011，乘数，从右往左一位一位的乘
   

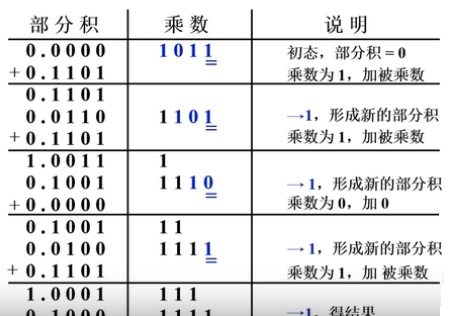
   • 乘积低位和乘数存在乘商寄存器中，将乘数低位顶掉
   • 乘积高位存在ACC寄存器中

3. 公式：
   
   
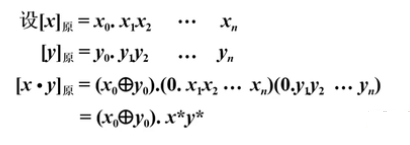
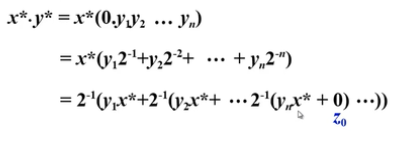
   符号由异或决定，绝对值相乘

4. 硬件配置示意图：
   

   • A：ACC寄存器，存放部分积（积的高位）
   • X：X寄存器，放被乘数
   • Q：MQ寄存器，存放乘数和部分积（积的低位）
   • 计数器C：记录移位次数
   • S：符号
   • GM：乘法标志
   • 移位和加受末位乘数控制

1.4 除法

1. 恢复余数法：
   
   

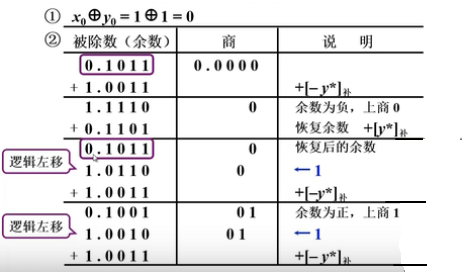
   • 余数为正，上商1，减除数
   • 余数为负，上商0，恢复余数

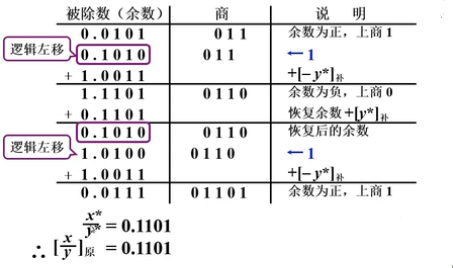
2. 加减交替法：

   • 规则：
     
     • R：余数
     • y：除数
   • 竖式：
     

3. 加减交替除法硬件配置：
   

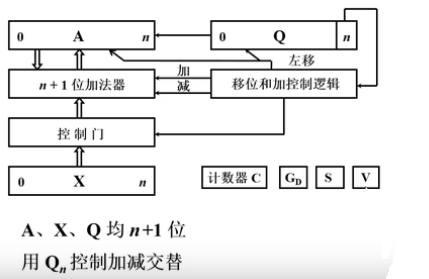
   • A：存放被除数，余数
   • X：存放除数
   • Q：存放商
   • GD：除法标志
   • V：溢出标志

2.浮点加减运算

步骤：对阶，尾数求和，规格化，舍入，溢出判断

2.1 对阶

小阶对大阶，右移：

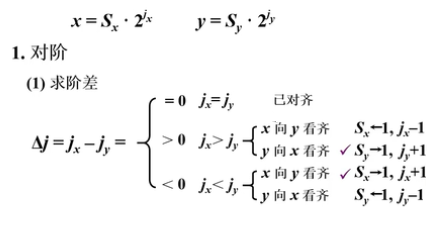
• 小阶对大阶
• 使阶数相同
• 左移高位丢失，误差大

2.2 尾数求和

将対阶过后的尾数相加即可：

2.3 (尾数)规格化

1. 规格化形式：基数为2

   • 原码：第一位数据位为1
   • 补码：第一位数据位和符号位不同

2. 尾数规格化：基数为2

   • 左归：尾数左移1位，阶码减1
   • 右归：尾数右移1位，阶码加1

3. 规格化数判断：
   

4. 特例：
   

   • S=-1无原码

2.4 舍入

対阶右规过程中，可能会出现尾数末位丢失的情况
数据长度超过最大值，低位(末位)部分处理:

• 0舍1入：处理的最高位为0，不处理，为1，当前尾数加1
• 全1法：不管处理的最高位为多少，当前尾数末位都变为1

2.5 溢出判断

3.ALU

1. ALU电路：
   
   组合逻辑电路，操作ki不同，输出Fi也不同
2. 并行加法器：
   

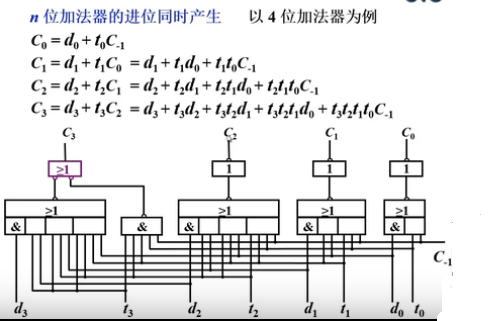
3.1 进位链

1. 串行进位链：
   

2. 并行进位链
   

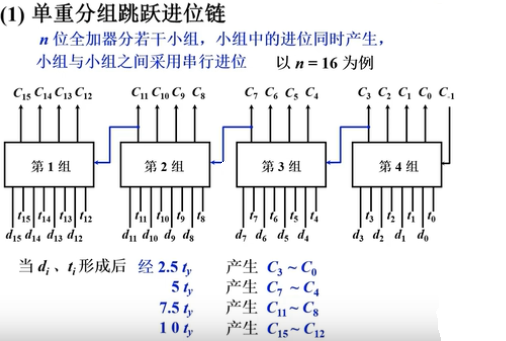
   • 单重分组跳跃进位链
     

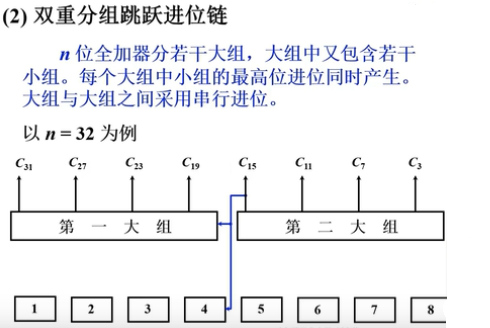
   • 双重分组跳跃进位链