暑假集训Day1 A(gcd)

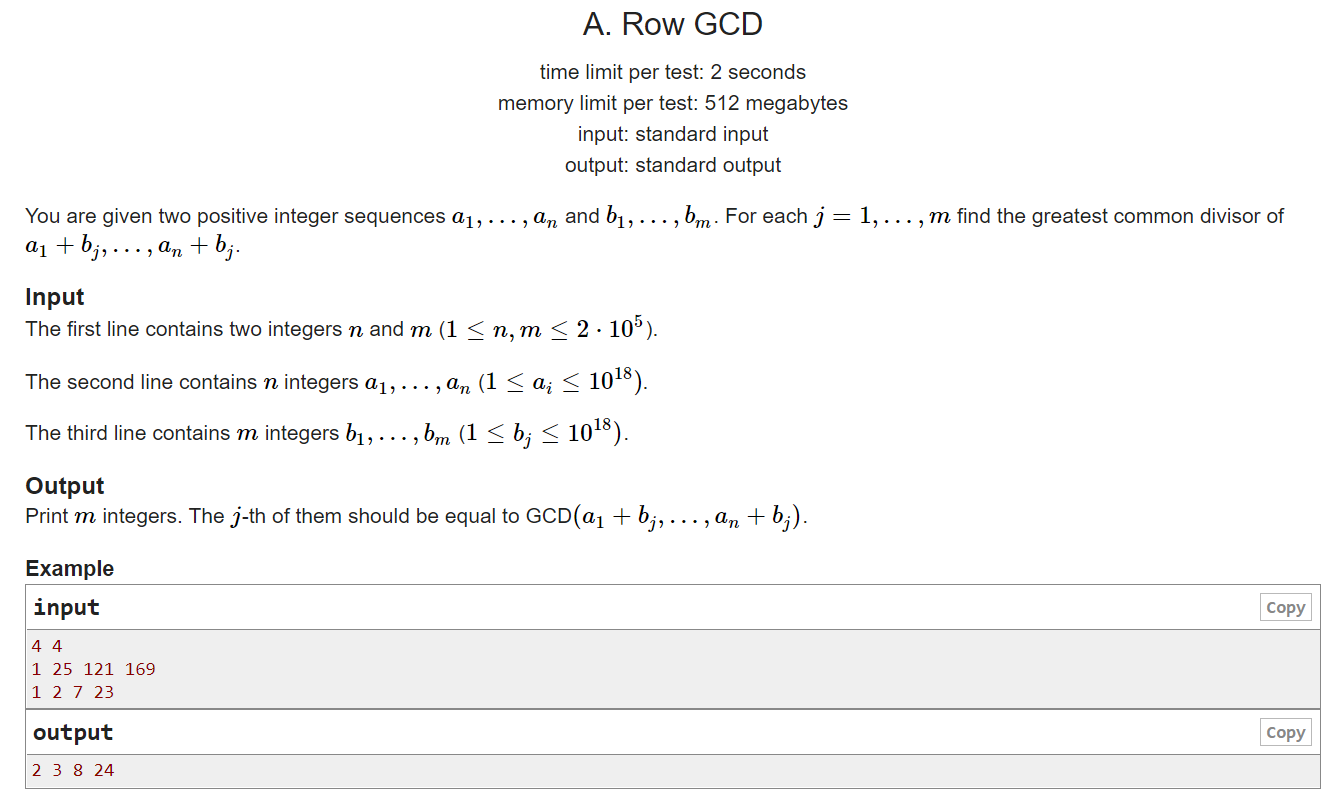
 这题一开始看到解多元方程组然后就直接想到中国剩余定理去了，事实上我们应该想到辗转相除法会把这里每个数多出来的数减掉，然后模拟一下辗转相除法，拿最小的数去把其他的数多出来的消掉，这样每次有n-1个数是固定的了。

对于中国剩余定理和扩展CRT都是要保证每一个方程组中的模数和余数是知道的，我们才能去算那个类lcm，此题如果列成方程组的话未知数过多，显然不是CRT的解法

#include "bits/stdc++.h"
using namespace std;
typedef long long LL;
const int MAX=2e5+5;
LL n,m,a[MAX],b[MAX],c;
inline LL gcd(LL x,LL y){
    return (y==0?x:gcd(y,x%y));
}
int main(){
    freopen ("a.in","r",stdin);
    freopen ("a.out","w",stdout);
    LL i,j;
    scanf("%lld%lld",&n,&m);
    for (i=1;i<=n;i++) scanf("%lld",a+i);
    for (i=1;i<=m;i++) scanf("%lld",b+i);
    sort(a+1,a+n+1);
    for (i=2;i<=n;i++) a[i]-=a[1];
    for (c=a[2],i=3;i<=n;i++)
        c=gcd(c,a[i]);
    for (i=1;i<=m;i++)
        printf("%lld ",gcd(c,a[1]+b[i]));
    return 0;
}