克隆图
克隆一张无向图,图中的每个节点包含一个 label (标签)和一个 neighbors (邻接点)列表 。
OJ的无向图序列化:
节点被唯一标记。
我们用 # 作为每个节点的分隔符,用 , 作为节点标签和邻接点的分隔符。
例如,序列化无向图 {0,1,2#1,2#2,2}。
该图总共有三个节点, 被两个分隔符 # 分为三部分。
- 第一个节点的标签为 0,存在从节点 0 到节点 1 和节点 2 的两条边。
- 第二个节点的标签为 1,存在从节点 1 到节点 2 的一条边。
- 第三个节点的标签为 2,存在从节点 2 到节点 2 (本身) 的一条边,从而形成自环。
我们将图形可视化如下:
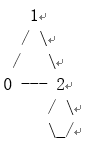
1 public class Solution { 2 public UndirectedGraphNode cloneGraph(UndirectedGraphNode node) { 3 if(node==null) 4 return null; 5 Queue<UndirectedGraphNode> q=new LinkedList<UndirectedGraphNode>(); 6 HashMap<UndirectedGraphNode,UndirectedGraphNode> hash=new HashMap<UndirectedGraphNode,UndirectedGraphNode>(); 7 UndirectedGraphNode graph=new UndirectedGraphNode(node.label); 8 q.add(node); 9 hash.put(node,graph); 10 while(!q.isEmpty()){ 11 UndirectedGraphNode curNode=q.poll(); 12 List<UndirectedGraphNode> currNeighbos=curNode.neighbors; 13 for(UndirectedGraphNode myNode: currNeighbos){ 14 if(!hash.containsKey(myNode)){ 15 UndirectedGraphNode copy=new UndirectedGraphNode(myNode.label); 16 hash.put(myNode,copy); 17 hash.get(curNode).neighbors.add(copy); 18 q.add(myNode); 19 }else{ 20 hash.get(curNode).neighbors.add(hash.get(myNode)); 21 } 22 } 23 } 24 return graph; 25 } 26 27 }