最小高度树
对于一个具有树特征的无向图,我们可选择任何一个节点作为根。图因此可以成为树,在所有可能的树中,具有最小高度的树被称为最小高度树。给出这样的一个图,写出一个函数找到所有的最小高度树并返回他们的根节点。
格式
该图包含 n 个节点,标记为 0 到 n - 1。给定数字 n 和一个无向边 edges 列表(每一个边都是一对标签)。
你可以假设没有重复的边会出现在 edges 中。由于所有的边都是无向边,[0, 1]和 [1, 0] 是相同的,因此不会同时出现在 edges 里。
示例 1:
输入: n = 4, edges = [[1, 0], [1, 2], [1, 3]]

输出: [1]
示例 2:
输入: n = 6, edges = [[0, 3], [1, 3], [2, 3], [4, 3], [5, 4]]
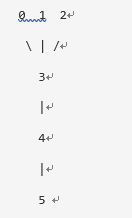
输出: [3, 4]
说明:
- 根据树的定义,树是一个无向图,其中任何两个顶点只通过一条路径连接。换句话说,一个任何没有简单环路的连通图都是一棵树。
- 树的高度是指根节点和叶子节点之间最长向下路径上边的数量。
解题思路
常规方法可以使用BFS或者DFS,对每个点都遍历一遍,求出所有点组成的树的高度,然后找出哪些高度最小的节点,可以通过不断更新最低高度来进行剪枝。但是时间复杂度过高。
最终的解题思路采用了不断删除叶子节点,逐渐逼近根节点的方法,在删除叶子节点的同时,会有一些新的节点成为叶子节点,于是继续循环删除,直至不能删除为止,那么剩下的节点就是高度最小的根。
首先将图存储起来,并将每个节点的入度存储起来,然后遍历将入度为1(叶节点)的节点加入队列。
bfs,当队列不空,取队列存储过的叶子节点再将叶子节点的邻接节点,如果邻接节点的度也为1(叶子节点),加入队列。
如此反复,直到减掉所有叶子节点最后一批剩下来的就是正确答案。
1 import java.util.ArrayDeque; 2 import java.util.ArrayList; 3 import java.util.List; 4 import java.util.Queue; 5 6 public class Solution { 7 public List<Integer> findMinHeightTrees(int n, int[][] edges) { 8 List<List<Integer>> map = new ArrayList<List<Integer>>(); 9 List<Integer> res = new ArrayList<Integer>(); 10 if (n==1) { 11 res.add(0); return res; 12 } 13 //记录每个点的入度 14 int[] degree = new int[n]; 15 for (int i = 0;i < n;i++ ) { 16 map.add(new ArrayList<Integer>()); 17 } 18 for (int i = 0;i< edges.length;i++) { 19 map.get(edges[i][0]).add(edges[i][1]); 20 map.get(edges[i][1]).add(edges[i][0]); 21 degree[edges[i][0]]++; 22 degree[edges[i][1]]++; 23 } 24 Queue<Integer> q = new ArrayDeque<Integer>(); 25 for (int i = 0;i < n;i++ ) { 26 if(degree[i] == 0) { 27 return res; 28 } else if(degree[i] == 1) { 29 q.offer(i); 30 } 31 } 32 while(!q.isEmpty()) { 33 res = new ArrayList<Integer>(); 34 int count = q.size(); 35 for (int i = 0;i < count ;i++ ) { 36 int cur = q.poll(); 37 res.add(cur); 38 degree[cur]--; 39 for (int k = 0;k < map.get(cur).size() ;k++ ) { 40 int next = map.get(cur).get(k); 41 degree[next]--; 42 if(degree[next] == 1) { 43 q.offer(next); 44 } 45 } 46 } 47 } 48 return res; 49 } 50 }