算法原理
参数更新公式(梯度下降)
[upsilon gets upsilon + Delta upsilon
]
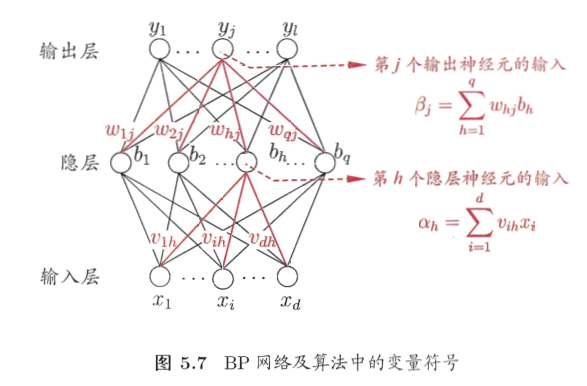
针对隐层到输出层的连接权

实际上,三层网络可以记为
[g_k(x) = f_2(sum_{j=1}^{l} omega_{kj} f_1(sum_{i=1}^{d} omega_{ji} x_i + omega_{j0}) + omega _{k0})
]
因此可继续推得
1.
[Delta heta_{j} = -eta frac{partial E_k}{partial heta_{j}} \
= -eta frac{partial E_k}{partial hat{y_j}^k} frac{{partial hat{y_j}^k}}{partial eta_j} frac{partial eta_j}{partial heta_j} \
= -eta g_j * 1\
= -eta g_j
]
[Delta V_{ih} = -etafrac{partial E_k}{partial hat{y_{1...j}}^k} frac{partial hat{y_{1...j}}^k}{partial b_n} frac{partial b_n}{partial alpha_n} frac{partial alpha_n}{partial v_{ih}} \
=-etasum_{j=1}^{l} frac{partial E_k}{partial hat{y_{j}}^k} frac{partial hat{y_{j}}^k}{partial b_n} frac{partial b_n}{partial alpha_n} frac{partial alpha_n}{partial v_{ih}} \
=-eta x_i sum_{j=1}^{l} frac{partial E_k}{partial hat{y_{j}}^k} frac{partial hat{y_{j}}^k}{partial b_n} frac{partial b_n}{partial alpha_n} \
= eta e_h x_i
]
[e_h = -sum_{j=1}^{l} frac{partial E_k}{partial hat{y_{j}}^k} frac{partial hat{y_{j}}^k}{partial b_n} frac{partial b_n}{partial alpha_n} \
= b_n(1-b_n) sum_{j=1}^{l} omega_{hj} g_j
]
可类似1得
[Delta gamma_h = -eta e_h
]


参考文献
《机器学习》,周志华著