来自:https://www.cnblogs.com/pinard/p/6131423.html
集成学习结合多个机器学习来完成学习任务。即“博采众长”。集成学习可用于分类问题集成,回归问题集成,特征选取集成,异常点检测集成等。可以说所有机器学习领域都可以看到集成学习的身影。
1. 集成学习概述
从下图看出集成学习对训练集我们训练若干个个体学习器,通过一定的结合策略,可以最终形成一个强学习器,达到博采众长的目的。
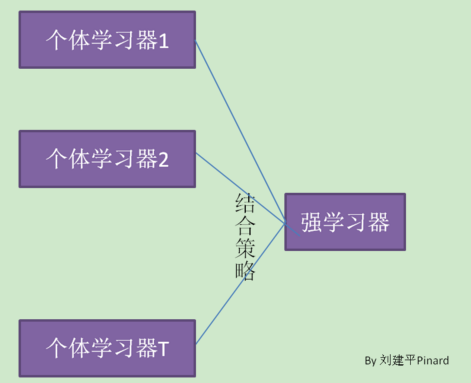
从这看出,集成学习有两个主要问题要解决,第一如何得到个体学习器;第二如何选择一种结合策略。
2. 集成学习的个体学习器
得到若干个个体学习器,有两种选择。
第一:所有的个体学习器都是一个种类的,或者说是同质的。比如都是决策树个体学习器,或者都是神经网络个体学习器。第二种是所有的个体学习器不全是一个种类,或者说是异质的。比如我们有一个分类问题,对训练集采用支持向量机个体学习器,逻辑回归个体学习器和朴素贝叶斯个体学习器来学习,再通过某种策略来确定最终的分类强学习器。
目前来说,同质个体学习器应用广泛。一般说的集成学习方法都是指同质个体学习器。而同质个体学习器使用最多的模型是决策树和神经网络。
同质个体学习器按照个体学习器之间是否存在依赖关系分为两类,
第一个是个体学习器之间存在强依赖关系,一系列个体学习器都需要串行生成,代表算法boosting算法,
第二个是个体学习器之间不存在强依赖关系,一系列个体学习器并行生成,代表算法bagging和随机森林(Random Forest)系列算法。
3. 集成学习之boosting
boosting的算法用一张图做一个概括如下:
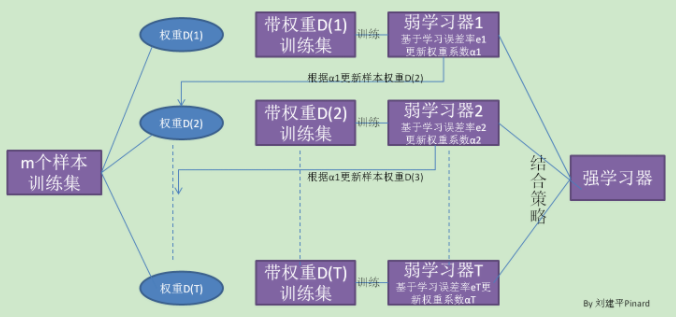
从图看出,Boosting算法的工作机制是首先从训练集用初始权重训练出一个弱学习器1,根据弱学习的学习误差率来更新训练样本的权重,使得之前弱学习器1学习误差率高的训练样本点的权重变高,使得这些误差率高的点在后面的弱学习器2中得到更多的重视。然后基于调整权重后的训练集来训练弱学习器2,如此重复进行,直到弱学习器数到达事先制定的数目T,最终将T个弱学习器通过集合策略进行整合,得到最终的强学习器。
Boosting系列算法最著名算法主要有AdaBoost算法和提升树(boosting tree)系列算法。提升树系列算法里有应用最广泛的是梯度提升树(Gradient Boosting Decision Tree)。
4. 集成学习之bagging
Bagging的算法原理与boosting不同,它的弱学习器之间没有依赖关系,可以并行生成,用一张图概括如下:

从上图可以看出,bagging的个体弱学习器的训练集是通过随机采样得到的。通过T次的随机采样,我们得到T个采样集,可以分别独立的训练出T个弱学习器,再对这T个弱学习器通过集合策略得到最终的强学习器。
这里的随机采样,一般采用的是自助采样法(Bootstap sampling),即有放回随机采样。这样每次采样集和原始训练集不同,和其他采样集也不同,这样得到多个不同的弱学习器。
随机森林是bagging的一个特化进阶版,所谓的特化是因为随机森林的弱学习器都是决策树。所谓的进阶是随机森林在bagging的样本随机采样基础上,又加上了特征的随机选择,其基本思想没有脱离bagging的范畴。
5. 集成学习之结合策略
假设得到的T个弱学习器是{h1, h2, h3,..., hT}
5.1 平均法
对于数值类的回归问题,常采用的集合策略是平均法。
1. 最简单的算术平均,最终预测是:
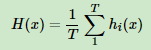
2. 每个弱学习器有权重w,最终预测是:
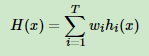
其中wi是弱学习器hi的权重,通常有:
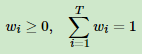
5.2 投票法
对于分类问题,常采用集合策略是投票法。
假设预测类别是{c1,c2,c3,...cK},对于任意一个预测样本x,我们的T个弱学习器的预测结果分别是(h1(x),h2(x),h3(x),...,hT(x))。
最简单的投票法是相对多数投票法,也就是我们常说的少数服从多数,也就是T个弱学习器对样本x的预测结果中,数量最多的类别ci为最终的分类类别。如果不止一个类别获得最高票,则随机选择一个做最终类别。
稍微复杂的投票法是绝对多数投票法,也就是我们常说的要票数过半。在相对多数投票法的基础上,不光要求最高票,还要票数过半。否则会拒绝预测。
更加复杂的是加权投票法,和加权平均法一样,每个弱学习器的分类票数要乘以一个权重,最终将各个类别的加权票数求和,最大的值对应的类别为最终类别。
5.3 学习法
学习法,代表方法stacking,当使用stacking的结合策略时,我们不是对弱学习器的结果做简单的逻辑处理,而是再加上一层学习器,也就是说,我们将训练集弱学习器的学习结果作为输入,将训练集的输出作为输出,重新训练一个学习器来得到最终结果。
这种情况下,我们将弱学习器称为初级学习器,将用于结合的学习器称为次级学习器。对于测试集,我们首先用初级学习器预测一次,得到次级学习器的输入样本,再用次级学习器预测一次,得到最终的预测结果。