除了计量值以外,还经常从成品率的角度分析生产中不合格品数或不合格品率。 这类检测数据称为计件值。
本篇介绍不合格品数控制图(np控制图)、不合格品率控制图(p控制图)、通用不合格品率控制图(Pr控制图)。
1. 不合格品数控制图(np图)
np 控制图用于监测工艺过程中不合格品数的起伏变化是否处于统计受控状态,一般每批样本数 n 固定不变。由于受监测的不合格品数等于每批样本大小 n 与不合格品率 p 的乘积 np,因此不合格品数控制图又称为 np 控制图。
1. np 控制图的控制限
确定不合格品数控制图控制限的方法也是 3σ 方法。
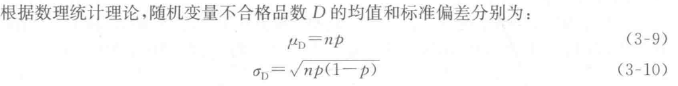
因此不合格品数控制图(np图)的中心线和上、下控制限为:
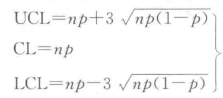

2. 不合格品数控制图应用实例
表4-6是某工序连续25批产品中不合格品数的统计数据,每批样本数 n = 100。
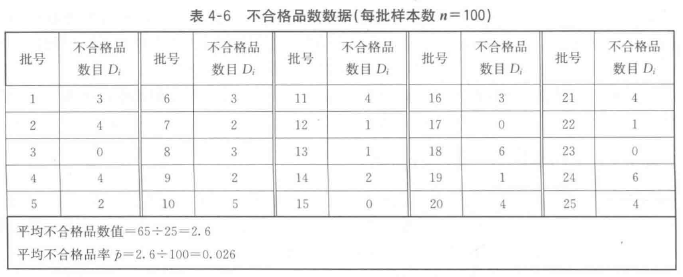
(1)分别计算25批不合格品数和不合格品率的平均值,如表4-6最后一行。
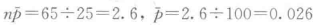
(2)采用式(4-22)计算np控制图的中心线和上下控制限。
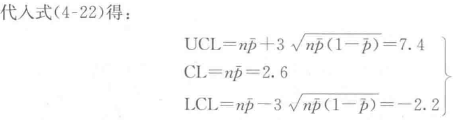
由于不合格品数不可能为负数,因此取下控制限 LCL = 0。
(3)绘制控制图:在控制图上画出中心线和上下控制限,同时将每批不合格数据标示在控制图上,即完成控制图的绘制。
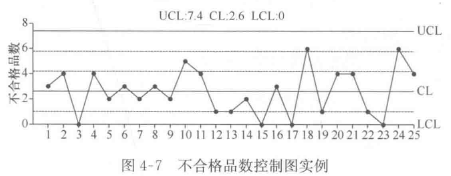
(4)按照(一)SPC与控制图 中给出的判断规则,查看是否存在失控情况。
2.不合格品率控制图(p图)
在每批样本数n不相等的情况下,先计算每批的不合格品率p,然后采用p控制图检测工艺成品率的变化情况。
1. 不合格品率控制图的控制限
确定不合格品率控制图控制限的方法也是 3σ 方法。

因此, 不合格品率控制图(p图)的中心线和上下控制限为:
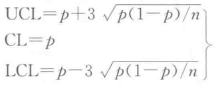

2. 不合格品率控制图应用实例
表4-7中为25批产品不合格品率的统计数据,每批样本数 n 互不相等。
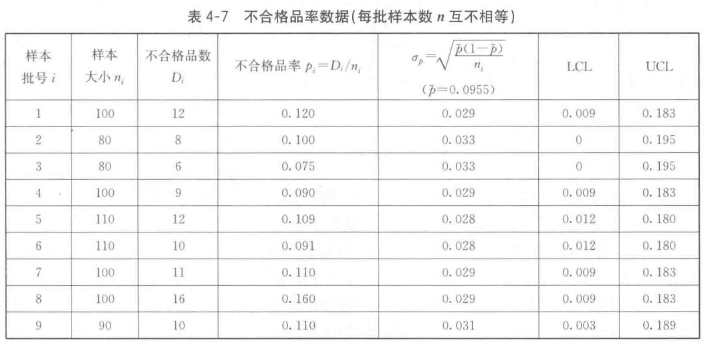

(1)分别计算每批的不合格品率 pi = Di/ni,结果如表第4列。
(2)计算25批不合格品率的平均值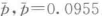 。
。
说明:由于每批样本量不相同,因此不合格品率的平均值应采用总的不合格品数除以总的样本量,而不是对25批不合格品率求平均值。
(3)采用式(4-23)计算p控制图的中心线和上、下控制限。

同理得到各批数据对应的上、下控制限。如果下控制限为负值,应取0。
(4)绘制控制图。可以看出每批的样本量不相同,所以UCL、LCL不是水平线,是折线。

按照判断规则,可以看出第11批数据点超出上控制限,属于失控状态。
2.通用不合格品率控制图(PT图)
1. 通用控制图
每批样本量 n 互不相同,导致上、下控制限不是一条水平线,而是折线。为了解决这个问题,采用下述“标准化”变换方法,将随机变量 p 变为 pT。

其中 μp 是随机变量 p 的均值,σp 是随机变量 p 的标准差。这里的 pT 有以下特点:均值为0,标准差为1。
按照 3σ 法则,采用式(4-24)变换后,得到中心线、上、下控制限为:
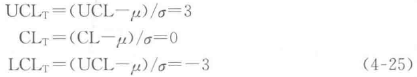
可以看出控制中心线为0,上、下控制限为常数3和-3,是取值固定而与原始数据无关的水平线,这种控制图称为通用控制图。
2. 通用不合格品率控制图(PT图)的具体实例
随机变量 p 的均值和标准差分别为:

对表4-7中的数据做“标准化”转换后得到表4-8的右两列。

在中心线为0,上、下控制限为3和-3的控制图中标出每批对应的 pT 值,得到 PT 控制图。
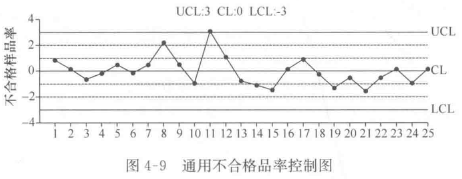
可以看出,第11批数据点刚好超出上控制限,属于失控状态。
3. 通用不合格品率控制图的优缺点
优点:作为“通用”控制图,不管每批样本量是否相同,控制图的中心线、上、下控制限分别为0,3,-3的水平线。给受控状态分析带来方便。
缺点:
1. 对每批数据进行标准化比较麻烦。
2. 控制图上出现的数据是变换后的数据,不是原始数据。因此很难将控制图上数据点的变化情况与实际结果相联系,从而解释困难。