渗透理论

1.渗透理论是研究随机环境中聚簇现象的理论。

渗透现象刚好出现的概率是临界概率，记做pc。当每条边开通的概率大于pc时，渗透就会出现，开通的概率小于pc，渗透不会出现。

人们在随机图理论的研究中发现节点存在节点集群的临界概率，即网络具有临界概率pc，当不超过pc时，网络由孤立的节点集群组成，当超过pc时，节点集群将扩展连接到整个网络。

2.模型建立（二维平面上的模型建立）

现实生活中很多问题可以用渗透理论合理解释：

(1).病毒传播在人群中的传播问题，一个病人单位时间以概率p感染他的邻居，受到感染的邻居又以概率p继续感染邻居，以此类推，如果感染概率p小于渗透出现的临界概率pc，大于临界概率pc，疾病将大范围传播。

(2).一块空地两部分，一部分沙子，一部分黏土。一场大雨过后，沙子那部分没存水，另一部分会存水。

参数p属于[0, 1]，当p=0，每条边都是闭合的，不存在可以延伸到无限远的开通路径。p=1，每条边都是开通的，这样一定存在延伸到无限远的开通路径。这两种情况都是没研究价值的，下面讨论当0<p<1的情况。

当p很小的时候，开通的边少，开通的路径会非常短。随着p的增加，开通的边逐渐增多，最终会延伸到无限远处的路径。下面是p=0.3和p=0.6的两种情况：

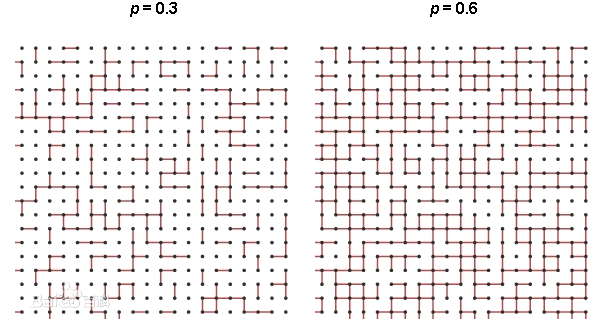
3.模型计算

渗透理论在二叉树上的表现

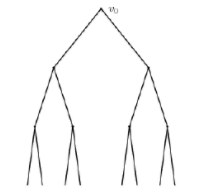
如果，p是每条边开通的概率，我们将找到Q(p)，这是存在一个可以包含根节点V₀并且延伸到无限远处的通路的临界概率。P_n表示存在一条从根节点V₀到第n层的概率，可以猜测,P_n是和n有关的一个函数，这样对n取极限就可以得到临界概率Q(p)。

我们发现P₀ = 1（其实是第0层的概率），下图是从根节点到第三层的情况。

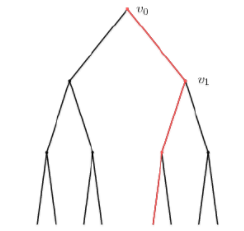
假设这条通路经过V₁，从V₀到第n层的概率是PP_n-1（P_n-1表示从V₁到第n层的概率）这样的话没有这么一条经过V₁到第n层的通路的概率是1-PP_n-1.

那么这条通路不经过V₀的概率是：（1-PP_n-1）²

所以存在这么一条经过V₀到达第n层的概率是：P_n = 1-（1-PP_n-1）²

设函数