在一个 2^k * 2^k 个方格组成的棋盘中,若恰有一个方格与其它方格不同,则称该方格为一特殊方格,称该棋盘为一特殊棋盘。显然特殊方格在棋盘上出现的位置有 4^k 种情形。因而对任何 k>=0 ,有 4^k 种不同的特殊棋盘。下图所示的特殊棋盘为 k=2 时 16 个特殊棋盘中的一个。

在棋盘覆盖问题中,要用下图中 4 中不同形态的 L 型骨牌覆盖一个给定的特殊棋牌上除特殊方格以外的所有方格,且任何 2 个 L 型骨牌不得重叠覆盖。易知,在任何一个 2^k * 2^k 的棋盘中,用到的 L 型骨牌个数恰为 (4^k-1)/3 。
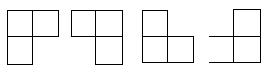
用分治策略,可以设计解棋盘问题的一个简捷的算法。
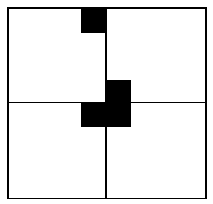
当 k>0 时,将 2^k * 2^k 棋盘分割为 4 个 2^(k-1) * 2^(k-1) 子棋盘,如下图所示。

特殊方格必位于 4 个较小子棋盘之一中,其余 3 个子棋盘中无特殊方格。为了将这 3 个无特殊方格的子棋盘转化为特殊棋盘,我们可以用一个 L 型骨牌覆盖这 3 个较小的棋盘的汇合处,如下图所示,这 3 个子棋盘上被 L 型骨牌覆盖的方格就成为该棋盘上的特殊方格,从而将原问题化为 4 个较小规模的棋盘覆盖问题。递归的使用 这种分割,直至棋盘简化为 1x1 棋盘。
下面给出代码:
1 #include<iostream>
2 #include<string.h>
3 using namespace std;
4 int tile=1; //L型骨牌的编号(递增)
5 int board[100][100]; //棋盘
6 /*****************************************************
7 * 递归方式实现棋盘覆盖算法
8 * 输入参数:
9 * tr--当前棋盘左上角的行号
10 * tc--当前棋盘左上角的列号
11 * dr--当前特殊方格所在的行号
12 * dc--当前特殊方格所在的列号
13 * size:当前棋盘的:2^k
14 *****************************************************/
15 void chessBoard ( int tr, int tc, int dr, int dc, int size )
16 {
17 if ( size==1 ) //棋盘方格大小为1,说明递归到最里层
18 return;
19 int t=tile++; //每次递增1
20 int s=size/2; //棋盘中间的行、列号(相等的)
21 //检查特殊方块是否在左上角子棋盘中
22 if ( dr<tr+s && dc<tc+s ) //在
23 chessBoard ( tr, tc, dr, dc, s );
24 else //不在,将该子棋盘右下角的方块视为特殊方块
25 {
26 board[tr+s-1][tc+s-1]=t;
27 chessBoard ( tr, tc, tr+s-1, tc+s-1, s );
28 }
29 //检查特殊方块是否在右上角子棋盘中
30 if ( dr<tr+s && dc>=tc+s ) //在
31 chessBoard ( tr, tc+s, dr, dc, s );
32 else //不在,将该子棋盘左下角的方块视为特殊方块
33 {
34 board[tr+s-1][tc+s]=t;
35 chessBoard ( tr, tc+s, tr+s-1, tc+s, s );
36 }
37 //检查特殊方块是否在左下角子棋盘中
38 if ( dr>=tr+s && dc<tc+s ) //在
39 chessBoard ( tr+s, tc, dr, dc, s );
40 else //不在,将该子棋盘右上角的方块视为特殊方块
41 {
42 board[tr+s][tc+s-1]=t;
43 chessBoard ( tr+s, tc, tr+s, tc+s-1, s );
44 }
45 //检查特殊方块是否在右下角子棋盘中
46 if ( dr>=tr+s && dc>=tc+s ) //在
47 chessBoard ( tr+s, tc+s, dr, dc, s );
48 else //不在,将该子棋盘左上角的方块视为特殊方块
49 {
50 board[tr+s][tc+s]=t;
51 chessBoard ( tr+s, tc+s, tr+s, tc+s, s );
52 }
53 }
54
55 int main()
56 {
57 int size;
58 memset(board,0,sizeof(board));
59 cout<<"输入棋盘的size(大小必须是2的n次幂): ";
60 cin>>size;
61 int index_x,index_y;
62 cout<<"输入特殊方格位置的坐标: ";
63 cin>>index_x>>index_y;
64 cout<<board[index_x][index_y]<<endl;
65 chessBoard ( 0,0,index_x,index_y,size );
66 for ( int i=0; i<size; i++ )
67 {
68 for ( int j=0; j<size; j++ )
69 cout<<board[i][j]<<' ';
70 cout<<endl;
71 }
72 return 0;
73 }