拓扑排序的定义:
把每个变量看成一个点,”小于“或者”先后“关系看成有向边,则我们得到一个有向图。这样我们的任务实际上是把一个图的所有节点排序,使每一条有向边的(u,v)对应的u都排在v之前,在图论中,我们称之为拓扑排序。不难发现,如果一个有向图里存在回路,则不存在拓扑排序(如果设置一个标志数组,我们可以发现回路中的点一直处于正在被访问状态,这可以作为拓扑排序的结束条件)。
我们先看一个样例:

下面我们用邻接矩阵存储这张图:
|
0 |
1 |
2 |
3 |
|
|
0 |
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
1 |
|
2 |
0 |
0 |
0 |
1 |
|
3 |
0 |
0 |
0 |
0 |
下面我们看看程序输出的结果:
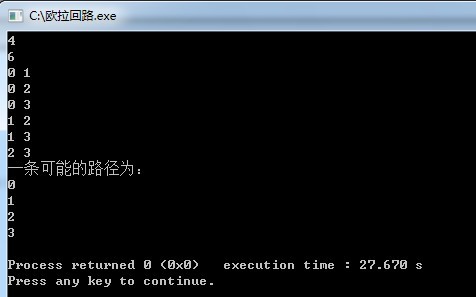
可见我们输出的路径只是很多情况中的一种。
下面附上ac代码:
1 #include<iostream> 2 #include<string.h> 3 using namespace std; 4 #define maxn 1000 5 int g[maxn][maxn],c[maxn],n,m,t; 6 bool dfs(int u) 7 { 8 c[u]=-1; 9 for(int v=0;v<n;v++) 10 if(g[u][v]) 11 { 12 if(c[v]<0) return false;//存在环路 13 else if(!c[v]) dfs(v); 14 } 15 c[u]=1;//访问完毕,标记为已经被访问 16 c[--t]=u;//把该节点入栈(此时t!=n,因为已经在递归调用的过程中使t减小了) 17 return true; 18 } 19 bool toposort() 20 { 21 t=n; 22 memset(c,0,sizeof(c)); 23 for(int v=0;v<n;v++) 24 if(!c[v]) 25 if(!dfs(v)) return false;//存在回路,不能进行拓扑排序 26 return true; 27 } 28 int main() 29 { 30 cin>>n>>m; 31 int u,v; 32 memset(g,0,sizeof(g)); 33 for(int i=1;i<=m;i++) 34 { 35 cin>>u>>v; 36 g[u][v]=1;//读入数据,即输入路径 37 } 38 if(toposort())//不存在回路,输出路径,这里只是很多路径的一种 39 { 40 cout<<"一条可能的路径为:"<<endl; 41 for(int i=0;i<n;i++) 42 cout<<c[i]<<endl; 43 } 44 else cout<<"no"<<endl; 45 return 0; 46 47 }