UVA 11401【数三角形】Triangle Counting------2015年1月24日

1.题意描述

给定边长为1,2,3，····n的n条边，现在要在里面任意选取三条边构成三角形，我们需要求一共可以构成多少个三角形？

2.题目分析

首先我们分析数据大小问题，由于数据最大可以达到10^6。所以我们如果直接枚举时间复杂度可以达到O(n^3)，那么我们可以肯定的说这个时间复杂度肯定是不能承受的。

那么我们可以根据前面求整理的排列组合公式的求二项式系数的方法联想到使用递推法。这样时间复杂度可以降低到O(n)。这是可以承受的。要想用递推法，我们肯定需要使用打表的方法，那么空间复杂度肯定是O(n)同样可以承受。现在我们分析怎样使用递推法：

我们先定义一个函数f(n)：当最大编程为n时所能构成的三角形数目。

对于三角形的三边而言，我们可以设定为x,y,z。并且我们假设x是最大边。那么我们有y+z>x，因此可以推出x-y<z<x。

根据这个不等式我们有，当y=1时，显然无解；当y=2时，有一个解；当y=3时，有两个解；·····当y=x-1时有x-2个解。根据等差数列求和公式我们有一共有

0+1+2+······+(x-2)=(x-1)(x-2)/2。但是我们需要注意，这里包含了y=z情况。那么我们需要减去从y=x/2+1开始到y=x-1为止，此时我们多计数了(x-1)-(x/2+1)+1=(x-1)/2个解，而且除此之外，我们对于每一个y我们都有重复计数，因为前后是对称的。所以我们最后还要除以2得到最终结果。

最终结果为：

          

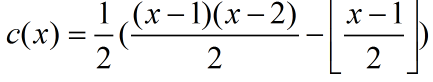
那么最后的递推式我们可以写为：

          

到这里基本分析完毕。

3.AC代码

#include<iostream>
#include<algorithm>//注意头文件的使用
#include<string.h>
using namespace std;
#define maxn 1000000+5
long long f[maxn];
void process()//函数预处理过程相当于打表这样节省时间
{
    memset(f,0,sizeof(f));
    for(long long  i=4;i<maxn;i++)
        f[i]=f[i-1]+((i-1)*(i-2)/2-(i-1)/2)/2;
}
int main()
{
    long long  n;
    process();
    while(cin>>n&&n)
    {
        if(n<3) break;//这里的坑不要往下跳！！！
      cout<<f[n]<<endl;
    }
    return 0;
}

4.总结

对于数据比较大的题型，特别是可以找到数学规律的题目我们可以采取研究递推公式进而简化时间复杂度，提高效率。