在图形图像编程时,我们常常需要根据一系列已知点坐标来确 定一条光滑曲线。其中有些曲线需要严格地通过所有的已知点,而有些曲线却不一定需要。在后者中,比较有代表性的一类曲线是贝塞尔曲线(Bézier Splines)。
网友们可能注意到,贝塞尔曲线广泛地应用于很多图形图像软件中,例如Flash、Illstrator、CoralDRAW和Photoshop等等。什么是贝塞尔曲线呢?你先来看看这个:
哼~一条很普通的曲线,好像真的无法给我们带来什么特殊感觉哦~那把这条曲线和绘制它所根据的点重叠地放在一起再瞧瞧吧:
Hoho,原来呀~贝塞尔曲线就是这样的一条曲线,它是依据四个位置任意的点坐标绘制出的一条光滑曲线。我们不妨把这四对已知点坐标依次定义成(x0,y0)、(x1,y1)、(x2,y2)和(x3,y3)。贝塞尔曲线必定通过首尾两个点,称为端点;中间两个点虽然未必要通过,但却起到牵制曲线形状路径的作用,称作控制点。
在历史上,研究贝塞尔曲线的人最初是按照已知曲线参数方程来确定四个点的思路设计出这种矢量曲线绘制法。涕淌为了向大家介绍贝塞尔曲线的公式,也故意把问题的已知和所求颠倒了一下位置:如果已知一条曲线的参数方程,系数都已知,并且两个方程里都含有一个参数t,它的值介于0、1之间,表现形式如下所示:
x(t) = ax * t ^ 3 + bx * t ^ 2 + cx * t + x0
y(t) = ay * t ^ 3 + by * t ^ 2 + cy * t + y0
由于这条曲线的起点(x0,y0)是已知的,我们可以用以下的公式来求得剩余三个点的坐标:
x1 = x0 + cx / 3
x2 = x1 + ( cx + bx ) / 3
x3 = x0 + cx + bx + ax
y1 = y0 + cy / 3
y2 = y1 + ( cy + by ) / 3
y3 = y0 + cy + by + ay
你细细观察一下就知道了,无论方程的已知和所求是什么,总是有六个未知数,并且我们总能找到六个等式(记住(x0,y0)总是已知的),也就是说,上面的方法是完全可逆的,因此我们可以根据四个已知点坐标来反求曲线参数公式的系数。稍微一变换就得到了下面这组公式:
cx = 3 * ( x1 - x0 )
bx = 3 * ( x2 - x1 ) - cx
ax = x3 - x0 - cx - bx
cy = 3 * ( y1 - y0 )
by = 3 * ( y2 - y1 ) - cy
ay = y3 - y0 - cy - by
所以说,对于坐标任意的四个已知点,你总能创建一条贝塞尔曲线嘿嘿。在GDI+的2D图形函数库里,已经封装了贝塞尔曲线的绘制方法——就是Graphics类的DrawBezier()方法。DrawBezier()方法有很多个重载版本,很简单,而且在MSDN里有着详细的介绍,涕淌在此就不浪费口水了(包括DrawBeziers()也是一样)。不得不感叹的是,强大的GDI+允许一个不了解贝塞尔曲线数学背景的人也能轻而易举地绘制一条漂亮的贝塞尔曲线,对提高开发效率而言,这当然是件好事!
贝塞尔曲线的有趣之处更在于它的“皮筋效应”~也就是说,随着点有规律地移动,曲线将产生皮筋伸引一样的变换,带来视觉上的冲击。来,瞅瞅这张图吧![]() :
:
Windows默认的屏保里有一个“贝塞尔曲线”的程序,大家现在可以打开来欣赏一下。一组不断扭伸的曲线令观看的人感叹它们的变幻莫测,其实个中道理相当简单,程序里只是一群分好了组的、按规律移动的点,机器根据点的移动、按照上面的公式实时地计算出当前的贝塞尔曲线,并在电脑屏幕上绘制出来,如此没完没了地进行着……
上个世纪七十年代,法国数学家Pierre Bézier第一个研究了这种矢量绘制曲线的方法,并给出了详细的计算公式,因此按照这样的公式绘制出来的曲线就用他的姓氏来命名~是为贝塞尔曲线。
在文章的开篇我提到了还有一类曲线必须严格地通过所有已知点,很典型而鲜明地同贝塞尔曲线区分开来了。这一类型的曲线涕淌将占用其它网络日志的篇幅来给大家介绍,请耐心等待![]() !
!
Trackback: http://tb.blog.csdn.net/TrackBack.aspx?PostId=299008
-------------------------------------------------------------------------------------------------------------------
“贝赛尔”工具在photoshop中叫“钢笔工具”;在CorelDraw中翻译成“贝赛尔工具”;而在Fireworks中叫“画笔”。它是用来“画线”造型的一种专业工具。当然还有很多工具也可以完成画线的工作,例如大家常用的photoshop里的直线、喷枪、画笔工具,Fireworks里的直线、铅笔和笔刷工具,CorelDraw里的自由笔,手绘工具等等。
用“贝塞尔”工具无论是画直线或是曲线,都非常简单,随手可得。其操作特点是通过用鼠标在面板上放置各个锚点,根据锚点的路径和描绘的先后顺序,产生直线或者是曲线的效果。我们都知道路径由一个或多个直线段或曲线段组成。锚点标记路径段的端点。在曲线段上,每个选中的锚点显示一条或两条方向线,方向线以方向点结束。方向线和方向点的位置确定曲线段的大小和形状。移动这些元素将改变路径中曲线的形状,可以看右图。路径可以是闭合的,没有起点或终点(如圆圈),也可以是开放的,有明显的端点(如波浪线)。
贝塞尔曲线是我们大陆的叫法,英文名是Bézier Curve,港澳台称为貝茲曲線,新加坡马来西亚称为贝济埃曲线。
先看一下效果图: 点击这里查看动画效果
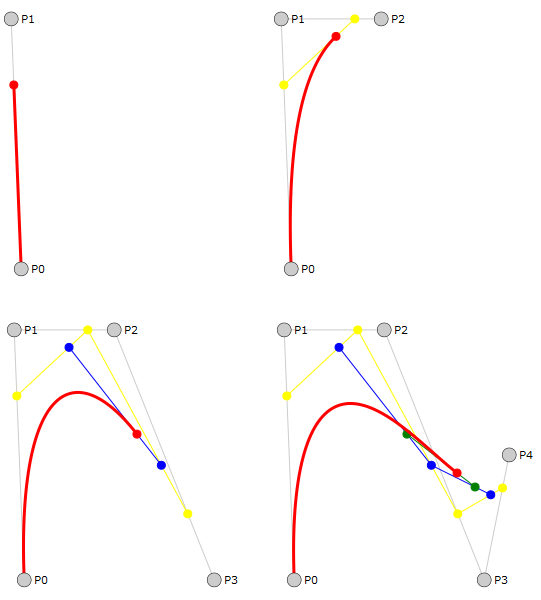
维基百科中的贝塞尔曲线条目中的几个GIF动画很漂亮,顺路贴上来。




下列程式码为一简单的实际运用范例,展示如何使用C标出三次方贝塞尔曲线。注意,此处仅简单的计算多项式系数,并读尽一系列由0至1的t值;实践中一般不会这么做,递归求解通常会更快速——以更多的内存为代价,花费较少的处理器时间。不过直接的方法较易于理解并产生相同结果。以下程式码已使运算更为清晰。实践中的最佳化会先计算系数一次,并在实际计算曲线点的循环中反复使用。此处每次都会重新计算,损失了效率,但程式码更清楚易读。
曲线的计算可在曲线阵列上将相连点画上直线——点越多,曲线越平滑。
在部分架构中,下以程式码也可由动态规划进行最佳化。举例来说,dt是一个常数,cx * t则等同于每次反复就修改一次常数。经反复应用这种最佳化后,循环可被重写为没有任何乘法(虽然这个过程不是稳定数值的)。
- /*
- 產生三次方貝茲曲線的程式碼
- */
- typedef struct
- {
- float x;
- float y;
- }
- Point2D;
- /*
- cp在此是四個元素的陣列:
- cp[0]為起始點,或上圖中的P0
- cp[1]為第一個控制點,或上圖中的P1
- cp[2]為第二個控制點,或上圖中的P2
- cp[3]為結束點,或上圖中的P3
- t為參數值,0 <= t <= 1
- */
- Point2D PointOnCubicBezier( Point2D* cp, float t )
- {
- float ax, bx, cx;
- float ay, by, cy;
- float tSquared, tCubed;
- Point2D result;
- /*計算多項式係數*/
- cx = 3.0 * (cp[1].x - cp[0].x);
- bx = 3.0 * (cp[2].x - cp[1].x) - cx;
- ax = cp[3].x - cp[0].x - cx - bx;
- cy = 3.0 * (cp[1].y - cp[0].y);
- by = 3.0 * (cp[2].y - cp[1].y) - cy;
- ay = cp[3].y - cp[0].y - cy - by;
- /*計算位於參數值t的曲線點*/
- tSquared = t * t;
- tCubed = tSquared * t;
- result.x = (ax * tCubed) + (bx * tSquared) + (cx * t) + cp[0].x;
- result.y = (ay * tCubed) + (by * tSquared) + (cy * t) + cp[0].y;
- return result;
- }
- /*
- ComputeBezier以控制點cp所產生的曲線點,填入Point2D結構的陣列。
- 呼叫者必須分配足夠的記憶體以供輸出結果,其為<sizeof(Point2D) numberOfPoints>
- */
- void ComputeBezier( Point2D* cp, int numberOfPoints, Point2D* curve )
- {
- float dt;
- int i;
- dt = 1.0 / ( numberOfPoints - 1 );
- for( i = 0; i < numberOfPoints; i++)
- curve[i] = PointOnCubicBezier( cp, i*dt );
- }
另一种贝塞尔曲线的应用是在动画中,描述物件的运动路径等等。此处,曲线的x、y位置不用来标示曲线,但用来表示图形位置。当用在这种形式时,连续点之间的距离会变的更为重要,且大多不是平均比例。点将会串的更紧密,控制点更接近每一个点,而更为稀疏的控制点会散的更开。如果需要线性运动速度,进一步处理时就需要循所需路径将点平均分散。
